Cenni di Statica del Corpo Rigido - Cattaneo

Appunti
CENNI SULLA STATICA DEL CORPO RIGIDO
Corso di Fisica e Laboratorio – prof. Massimo Manvilli
SEZIONE ITI
ITCG Cattaneo con Liceo Dall’Aglio
Castelnovo ne’ Monti (RE) via G. Impastato n.3
CORPO RIGIDO :
Corpo solido, esteso, idealmente indeformabile . Le distanze tra le molecole che lo compongono si
mantengono inalterate sia quando il corpo è in quiete che quando è in movimento.
In realtà non esistono corpi perfettamente rigidi.
Vengono considerati perfettamente rigidi corpi che sotto l’azione di una o più forze presentano
deformazioni di entità talmente piccola da poter essere considerata trascurabile.
Valutare l’effetto di forze applicate ad un corpo rigido è più complesso rispetto al caso di forze applicate ad
un punto materiale (forze applicate tutte nello stesso punto).
Nel caso del C.R. infatti le forze possono essere applicate in punti differenti, anche molto distanti tra loro e
questo può avere un effetto particolarmente rilevante.
Punto Materiale
Corpo Rigido
F4
F3
F3
F4
D
C
F2
B
F2
A
F1
F1
Per avere un’idea più precisa dell’effetto di un sistema di forze applicate in punti differenti di un C.R. si
ricorre, come nel caso del punto materiale, alla determinazione grafica della risultante.
Questa operazione appare piuttosto complessa in quanto la regola del parallelogrammo , già conosciuta ed
utilizzata, si può applicare solamente quando le forze hanno il medesimo punto di applicazione.
Fortunatamente per i C. R. vale una proprietà che può ricondurre il problema al caso di forze con lo stesso
punto di applicazione.
Nella figura a fianco vediamo un C.R. a cui sono applicate due forze
esattamente uguali e contrarie in due punti differenti A e B ;
evidentemente il corpo si trova in equilibrio .
E’ facilmente verificabile che facendo scorrere entrambe le forze verso
l’esterno, fino a due nuovi punti di applicazione A’ e B’ , il corpo rimane
in equilibrio.
L’equilibrio viene mantenuto anche allontanando ancora i punti di
applicazione delle due forze fino ad A” e B”. L’equilibrio si mantiene se i
punti di applicazione delle forze vengono spostati lungo la retta d’azione
delle forze stesse.
Questa proprietà, facilmente verificabile in questo caso semplice, vale in
generale per tutti i corpi rigidi.
A
F
A'
B
F
B'
F
F
A''
B''
F
F
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 1
In un Corpo Rigido è possibile far scorrere le forze lungo la loro retta d’azione
in quanto il loro effetto sul corpo stesso non cambia.
Vediamo come questa proprietà può consentire la semplice costruzione
grafica della risultante di forze applicate ad un corpo rigido utilizzando
ancora la regola del parallelogrammo..
In figura è rappresentato un C.R. cui sono applicate due forze nei punti A e B.
B
F2
A
F1
Sfruttando la proprietà precedente possiamo far scorrere entrambe le forze
lungo la loro retta d’azione fino a che i due punti A e B vengano a coincidere
nel punto di incrocio “O” delle rette d’azione delle forze.
O
O
F1
B
F2
O
R
R
F2
A
F1
Una volta portati i vettori fino al punto O potremo determinare la risultante delle due forze mediante la
regola del parallelogrammo.
Il C. R. si muoverà come se fosse applicata una sola forza uguale alla risultante R applicata nel punto O , o
in qualsiasi punto della sua retta d’azione. La risultante ci può dare un’idea più immediata di quale potrà
essere il movimento del corpo.
GRADI DI LIBERTA’ DI UN CORPO RIGIDO NEL PIANO
F
F
Con il termine “gradi di libertà” vengono indicati i movimenti
elementari che un c.r. può compiere nel piano.
I movimenti che un C.R. può effettuare nel piano sono
sostanzialmente due : uno spostamento ed una rotazione.
Una forza applicata ad un corpo rigido può quindi produrre questi due
effetti, a seconda del suo punto di applicazione.
Come vedremo una sola forza applicata può, in casi particolari
caratterizzati da perfetta simmetria (teoricamente possibili ma in
pratica difficilmente realizzabili), produrre un semplice spostamento
mentre non può produrre la sola rotazione del corpo.
Spostamento
Spostamento
+ rotazione
In generale quindi una forza applicata ad un corpo rigido nel piano produce uno spostamento accompagnato
da una rotazione. (vedi figura)
Di solito lo spostamento viene scomposto in una componente in direzione X ed un’altra in direzione Y ; per
questo motivo si può concludere che i gradi di libertà del C.R. nel piano sono tre :
-Spostamento in direzione X
-Spostamento in direzione Y
-Rotazione attorno ad un asse ortogonale al piano
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 2
Y
Y
Y
Y
R
Sy
Sy
Sx
Sx
R
Spostamento in direzione Y
Spostamento in direzione X
X
X
X
X
S
Rotazione
Caso generale
Per l’analisi dei movimenti di rotazione risulta fondamentale la conoscenza di una nuova grandezza fisica :
il “momento di una forza rispetto ad un punto” , di cui parleremo nel paragrafo seguente.
MOMENTO DI UNA FORZA RISPETTO AD UN PUNTO
Questa grandezza fisica è, come vedremo, di fondamentale importanza nella descrizione del moto
rotatorio di un C.R. e nella individuazione delle condizioni necessarie per avere equilibrio alla rotazione
(ovvero per capire in quali condizioni un c.r. non “gira”)
Daremo prima la definizione teorica di questa grandezza , mostrando poi successivamente alcuni esempi
pratici che ne evidenziano l’importanza.
P
b
ac
(br
cio
d
ta
ret
90°
)
ion
'az
Supponiamo di avere un forza applicata in un punto del piano ed un altro
punto P qualunque (senza preoccuparci del corpo su cui la forza è
effettivamente applicata).
Si chiama :
Momento della forza F rispetto al punto P :
prodotto tra l’intensità della forza ed il braccio della forza stessa
rispetto al punto P
z
for
ella
ed
M(p) = F*b
(N*m)
a
F
Braccio della forza F rispetto al punto P (= b) :
Distanza tra il punto P e la retta d’azione della forza F.
E’ la lunghezza del segmento che unisce il punto P alla
retta ed è ad essa perpendicolare.
(vedi figura a fianco)
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 3
Esaminiamo la situazione seguente in cui , applicando una forza, si deve aprire un pesante portone.
Proviamo ad esaminare la figura seguente in cui sono rappresentate tre situazione possibili.
Asse di
rotazione
CASO 1
CASO 3
CASO 2
Vista dall'alto
F
90°
90°
P
b
braccio
F
ES : F = 100 N
b = 0,90 m
Portone
da aprire
P
P
b=0
F
F
ES : F = 100 N
b = 0,00 m
ES : F = 100 N
b = 0,30 m
Il Momento prodotto dalla
forza rispetto all'asse di
rotazione del portone vale :
Il Momento prodotto dalla
forza rispetto all'asse di
rotazione del portone vale :
M = F*b = 100*0,90 = 90 Nm
M = F*b = 100*0,30 = 30 Nm
Il portone si apre ruotando intorno
all'asse che passa per i cardini
Il portone gira con molta più
difficoltà
Il Momento prodotto dalla
forza rispetto all'asse di
rotazione del portone vale :
M = F*b = 100*0,00 = 0 Nm
Questo per qualunque valore
della forza F
Quando il Momento è =0
il portone non gira
CASO 1
E’ quello più comune.
Le maniglie normalmente sono disposte in questa posizione per facilitare l’operazione di
apertura.
Il momento della forza F rispetto al punto P ha un valore abbastanza elevato ed il portone
ruota agevolmente attorno all’asse di rotazione che passa per i cardini .
CASO 2
Se spostiamo il punto di applicazione della forza più vicino all’asse di rotazione , riducendo il
braccio della forza rispetto al punto P, anche il valore del Momento diventa minore ed il
portone gira con molta maggior difficoltà.
Un basso valore del Momento della forza F rispetto al punto P produce quindi un movimento
rotatorio nettamente più lento e difficoltoso.
Per ottenere una rotazione come quella del caso precedente dovremmo aumentare il valore
della spinta fino ad ottenere lo stesso valore del momento ; sarebbe necessaria una forza di
300 N , infatti : b = 0,30 m
F = 300 N
M(p) = F*b = 300*0,30 = 90 Nm
CASO 3
Se spostiamo il punto di applicazione della forza in corrispondenza dell’asse di rotazione, in
modo che la retta d’azione della forza passi per il punto P (spingiamo sui cardini), possiamo
facilmente constatare che il portone non gira .
Il valore del momento della forza F rispetto al punto P vale zero in quanto vale zero il braccio
della F rispetto a P.
In questo caso il valore del momento risulterebbe nullo anche se noi aumentassimo il valore
della forza F ; anche spingendo con una forza elevatissima il portone non si muoverebbe.
Es : b = 0,00 m
F = 10000 N
M(p) = F*b = 10000*0,00 = 0,00 Nm
Quando il valore del momento è nullo il portone non gira.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 4
Esempio : La Pendola
P
P
b≠0
Per far ripartire la pendola del salotto portiamo la
massa sospesa nella posizione A e la lasciamo
libera.
La massa inizia a ruotare attorno al perno P in
quanto il valore del momento della forza agente
(peso) rispetto al punto P (perno) è diverso da
zero.
b=0
A
B
F
M(p) ≠ 0
La massa inizia a ruotare
attorno al punto P
F
M(p) = 0
La massa non ruota, ma
rimane ferma in questa
posizione
Se la massa sospesa viene posta nella posizione
B, come indicato in figura, e lasciata libera non
si verifica nessun movimento rotatorio attorno al
perno P, anzi il pendolo rimane fermo in quella posizione (in equilibrio).
E’ facile constatare che il braccio della forza rispetto al punto P è nullo ; di conseguenza è nullo anche
il valore del momento M(p) e la massa non ruota qualunque sia il suo valore.
Ciò che abbiamo visto in questi semplici esempi ha valore del tutto generale .
Riassumendo :
- Quando il Momento delle Forze agenti è
M=0
Il corpo non ruota
- Quando il Momento delle Forze agenti è
M≠0
Il corpo ruota
- Più è alto il valore del momento più “velocemente” avverrà la rotazione del corpo
- Quando la retta d’azione della forza passa per il punto P il braccio è nullo quindi anche il momento
è nullo per qualunque valore della forza F
Il verso dei Momenti , il Momento Risultante e l’equilibrio alla rotazione
Supponiamo che ci siano due persone che stanno spingendo
contemporaneamente il portone in due versi opposti spingendo
con la medesima forza ma in punti di applicazione differenti
come indicato nella figura a fianco.
F1 = 100 N
F2 = 100 N
b1 = 0,90 m
b1 = 0,45 m
Nonostante le due forze siano esattamente uguali e contrarie il
portone non è in equilibrio, come si potrebbe pensare, ma ruota
in senso antiorario.
Infatti, come abbiamo visto in precedenza, ciò che conta nel
caso dei moti rotatori è il valore del momento della forza e non
solamente il suo modulo.
F2
P
b2
b1
F1
Nel caso in figura possiamo constatare come il momento della forza F1 rispetto al punto P sia maggiore
di quello della forza F2 .
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 5
M1 = F1 * b1 = 100 * 0,90 = 90 Nm
M2 = F2 * b2 = 100 * 0,45 = 45 Nm
induce una rotazione antioraria
induce una rotazione oraria
Tutto funziona come se sul portone agisse una forza tale da
produrre un Momento antiorario
45 Nm
P
M= M1-M2 = 90 – 45 = 45 Nm
che viene definito Momento Risultante
I Momenti hanno quindi un verso .
Nel caso del movimento su un piano possono avere verso Orario o Antiorario.
Convenzionalmente , nel calcolo, ai due versi vengono attribuiti segni differenti; noi adotteremo la
convenzione seguente :
Momenti Antiorari
Positivi
+
Momenti Orari
Negativi
_
A questo punto potremmo calcolare quale valore della forza F2 sarebbe necessario per avere l’equilibrio
alla rotazione ovvero per fare in modo che il portone non ruoti attorno all’asse passante per il punto P.
Per avere equilibrio dovrà essere nullo il momento
risultante.
F2
P
Scriviamo l’espressione del momento risultante adottando la
convenzione sui segni indicata in precedenza in cui compare il
valore di F2 come incognita :
b2
b1
F1
Mris = - F2*0,45 + 100*0,90 = -F2*0,45 + 90
Per l’equilibrio il Momento Risultante deve essere nullo , cioè
dovrà essere :
-F2*0,45 + 90=0
ovvero
90 =+ F2*0,45
e dividendo ambo i membri per 0,45 si ottiene :
90/0,45 = F2
F2 = 200 N
Affinchè il momento della forza F2 diventi esattamente uguale ed opposto a quello della F1, in modo da
rendere nullo il Momento Risultante e mantenere in equilibrio il portone , si dovrà applicare una forza
F2=200 N.
In questo caso semplice possiamo constatare che affinchè il modulo dei momenti sia uguale ed il Momento
risultante sia nullo (visto che hanno verso e quindi segno opposto) la forza F2, che ha un braccio b2 pari alla
metà di b1, dovrà avere un valore doppio rispetto alla F1.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 6
E’ appena il caso di ricordare che nel caso del punto materiale la presenza di due forze uguali ed opposte
comporta sempre che la risultante sia nulla ed il punto rimanga in equilibrio, mentre per i corpi rigidi in
moto rotatorio questo non è sufficiente in quanto risulta molto importante la posizione del punto di
applicazione delle forze e, per questo motivo , ciò che conta è il valore dei momenti.
CONDIZIONI GENERALI DI EQUILIBRIO DI UN CORPO RIGIDO NEL PIANO
Si può dimostrare che affinchè un corpo rigido sia in equilibrio alla traslazione ed alla rotazione (quindi
“fermo”) devono verificarsi due condizioni :
F risultante = 0
questo garantisce che il corpo è in equilibrio alla traslazione
ovvero non si sposta ( non trasla)
M risultante = 0
questo garantisce che il corpo è in equilibrio alla rotazione
ovvero non ruota
Per un corpo rigido con un punto fisso (perno) è abbastanza evidente che
il momento risultante debba essere calcolato rispetto al punto fisso.
Non è altrettanto chiaro quale sia il punto rispetto al quale calcolare il
momento risultante se il c.r. non presenta alcun punto fisso nel piano
(corpo rigido libero).
2
F4
F3
D
C
3
4
B
In presenza di un corpo rigido libero , come quello in figura, si può
intuire come il momento risultante calcolato rispetto al punto 1 abbia un
valore diverso da quello calcolato rispetto al punto 2 o ai punti 3 e 4
(cambiano tutti i bracci delle forze).
F2
A
F1
1
Si può dimostrare che se il valore del momento risultante
( somma algebrica dei momenti di tutte le forze agenti) calcolato rispetto ad un punto , ad esempio il
punto 2, assume valore zero, allora vale sempre zero anche se viene calcolato rispetto ad un altro
punto qualsiasi del piano, come i punti 1, 3, 4.
Questa proprietà risulta molto utile quando si vuole verificare se un c.r. sottoposto a diverse forze, è in
equilibrio alla rotazione.
E’ sufficiente infatti calcolare il valore del momento risultante rispetto ad un punto qualsiasi ; se questo
vale zero allora il corpo rigido è in equilibrio alla rotazione, altrimenti no.
Le due condizioni precedenti devono essere verificate contemporaneamente
affinchè sia garantito l’equilibrio.
F
Esempio : Sul corpo in figura agiscono due forze uguali ed opposte ma con diverso
punto di applicazione.
F
Trattandosi di forze uguali ed opposte potremmo affermare che la risultante è nulla,
ma in effetti è facile verificare che il corpo non può stare fermo, quindi non è in
equilibrio, ma ruota in senso orario ( il momento risultante è ≠ 0 ).
Su questo caso particolarmente importante torneremo in seguito.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 7
Il Corpo rigido vincolato
Un corpo rigido è vincolato quando, per effetto di azioni esterne, alcuni suoi movimenti sono impediti.
E’ il caso, ad esempio, di un quadro appeso alla parete, una porta che può solamente ruotare intorno
all’asse passante per i cardini ecc.
I vincoli infatti, come il sostegno del quadro o i cardini della porta, esercitano sul corpo
R = - Fp forze che ne condizionano i movimenti chiamate Reazioni Vincolari
Fp
Vediamo un semplice esempio .
Nella figura a fianco è rappresentato un quadro appeso alla parete mediante un chiodo
metallico.
Il chiodo sotto l’azione del quadro si deforma ed esercita una forza elastica di richiamo
uguale e contraria al peso del quadro; la risultante delle forze è uguale a zero (e così
anche il Momento risultante) e quindi il quadro sta in equilibrio.
La reazione elastica del chiodo consiste quindi in una forza che agisce sul corpo e ne
impedisce lo spostamento verso il basso.
Nel calcolo della risultante e del momento risultante deve essere considerata anche
questa forza.
Vediamo un secondo esempio :
bR
Un’asta pesante viene incernierata al muro e
sostenuta da un appoggio all’estremità opposta.
bP
L’asta può ruotare attorno alla cerniera.
L’appoggio, compresso dall’asta, viene
deformato e reagisce con una forza elastica
P
MR
diretta verso l’alto. L’asta può rimanere in
MP
equilibrio in questa posizione in quanto il
R
momento della reazione dell’appoggio R
rispetto al fulcro è esattamente uguale ed
opposto a quello prodotto dalla forza peso applicata nel baricentro dell’asta. In questo caso, come abbiamo
imparato, il valore della reazione elastica dell’appoggio sarà minore del peso dell’asta in quanto può contare
su un braccio maggiore .
Riassumendo :
----------------------------------------------------------------------------------------------------------------------------------- Equilibrio di un punto materiale
Un punto materiale è in equilibrio quando la risultante delle
forze ad esso applicate è nulla ovvero Fris = 0
----------------------------------------------------------------------------------------------------------------------------------- Equilibrio di un corpo rigido libero
Un corpo rigido libero è in equilibrio quando la risultante
delle forze ad esso applicate è nulla ed è nullo anche il
momento risultante ovvero
Fris = 0
Mris = 0
---------------------------------------------------------------------------------------------------------------------------------- Equilibrio di un corpo rigido vincolato
Le condizioni di equilibrio di un corpo rigido vincolato
sono le stesse del corpo rigido libero a condizione che
vengano considerati gli effetti delle reazioni dei vincoli
---------------------------------------------------------------------------------------------------------------------------------
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 8
I Corpi appoggiati
Il corpo sta fermo.
Posizione di equilibrio
G
Lasciato libero il corpo
viene riportato nella
posizione di equilibrio
per effetto del
momento antiorario
(stabilizzante) della
forza Fp rispetto al
punto P.
Posizione limite
oltre la quale
l'equilibrio non è più
possibile
G
P
La retta d'azione della
forza peso va oltre il
punto P. Questa forza
determina un
momento orario
attorno al punto P
che provoca la
caduta del corpo
G
P
G
P
Finchè la retta d'azione della forza Fp (pensata agente nel baricentro G ) cade all'interno della base di
appoggio il corpo, lasciato libero, viene riportato nella posizione di equilibrio iniziale.
Quando la retta d'azione della Fp cade fuori della base di appoggio il momento della forza stessa diventa
“ribaltante” e l'oggetto cade sul tavolo.
E' evidente come un corpo appoggiato con baricentro basso e base larga sia molto più stabile di uno "alto e
stretto" .
-- Equilibrio dinamico - Esempio
-----------------------------------------------------------------------------------
Mentre la moto percorre la
curva agiscono , in senso
Fc
trasversale, diverse forze che
G
sono in equilibrio tra loro.
M (Fc)
Oltre alla forza peso, agisce la
Fr
cosiddetta forza centrifuga,
Fp
conosciuta da tutti, che è diretta
Fa
verso l’esterno della curva e
A
tende a far ribaltare il veicolo.
M (Fp)
r
F
Questo è il motivo per cui il
=
M(Ris) = M(Fc) M(Fp) = 0
R
pilota inclina la moto verso
Fterr
l’interno della curva ; in questo
modo il momento ribaltante dovuto alla forza centrifuga può essere annullato da quello stabilizzante della
forza peso rispetto all’appoggio A.
Il modulo della forza centrifuga aumenta con la velocità e per questo più la curva è veloce più è necessario
piegare la moto per aumentare il braccio della forza peso rispetto al punto A (visto che il suo modulo non
può cambiare) e far diminuire quello della forza centrifuga, trovando una nuova posizione di equilibrio.
Possiamo inoltre osservare che, a livello del terreno, agiscono due forze : la forza di attrito e la reazione
elastica del terreno. Queste due reazioni danno una risultante esattamente uguale e contraria a quella tra la
forza centrifuga e la forza peso, per cui le forze agenti sulla moto si annullano ; inoltre queste due risultanti
hanno la stessa retta d’azione quindi anche il momento risultante è nullo e la moto sta in equilibrio in senso
trasversale.
A volte purtroppo, per fatalità o per valutazioni troppo ottimistiche del pilota, la forza massima di attrito non
è più sufficiente a bilanciare l’effetto della forza centrifuga e la moto sbanda partendo” per la tangente”
ovvero perde aderenza.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 9
MACCHINE SEMPLICI - LE LEVE
Una leva è costituita da un corpo rigido , di solito snello ( ma non necessariamente), che può ruotare attorno
ad un punto fisso detto Fulcro . Viene di solito utilizzata per sollevare corpi pesanti.
Ad una estremità dell’asta si trova il corpo da sollevare , il cui peso viene indicato con il termine di Forza
Resistente, mentre all’altra estremità viene applicata la forza necessaria a sollevare il carico , indicata col
termine di Forza Motrice ( la forza che dobbiamo esercitare noi) .
Fr = Forza resistente
Fm = Forza Motrice
Fm = Forza Motrice
Fr = Forza Resistente (carico)
Fulcro
m = braccio della forza motrice
rispetto al fulcro
r = braccio della forza resistente
rispetto al fulcro
R = Reazione dell'appoggio
m
braccio della Fm
rispetto al fulcro
r
braccio della Fr
rispetto al fulcro
L’equilibrio alla rotazione della leva si verifica quando il
Momento Risultante delle forze applicate, calcolato rispetto al
fulcro, diventa nullo, ovvero quando il Momento della Forza
Motrice rispetto al fulcro è uguale e contrario a quello della
Forza Resistente. (stesso modulo ma verso opposto). Nel calcolo
del momento risultante dovrebbe essere inserito anche il
momento della reazione R dell’appoggio ma, poiché il braccio di
R rispetto al fulcro vale zero, tale momento risulta sempre nullo
indipendentemente dal valore della forza R stessa.
Fm
Con i semplici passaggi riportati qui a fianco è quindi possibile
ricavare la Condizione di Equilibrio della leva
M Fm
M Fr
m
Fr
r
R
Fm * m - Fr * r
+
R* 0 = 0
Fm * m - Fr * r = 0
Fm * m = Fr * r
Fm * m = Fr * r
Questa relazione può essere usata per determinare il valore della forza motrice necessaria ad equilibrare
un dato carico.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 10
-- Esempio 1 ----------------------------------------------------------------------------------------------------------Fr = 1000 N
Fm = ?
2,4 m
1,2 m
Supponiamo di voler calcolare quale Forza Motrice sia necessaria
per tenere in equilibrio la leva in figura, sottoposta all’azione di una
Forza Resistente di 1000 N, sapendo che il braccio di Fm rispetto al
fulcro vale bm = 2,40 m mentre quello della Fr vale br = 1,20 m
Dall’inversione della formula precedente si
ottiene :
R
quindi :
Fm = Fr . r
m
Fm = 1000* 1,2/2,4 = 500 N
Con una forza di 500 N riusciremmo ad equilibrarne una di 1000 N . Significa che spingendo con una Fm
= 500 N all’estremità sinistra della leva l’altra estremità spingerà verso l’alto con una forza uguale e
contraria al carico ovvero di 1000 N. La leva funziona quindi, in questo caso, come un amplificatore
della nostra forza ; in questo caso la leva viene definita “Vantaggiosa” .
Notiamo che siccome il braccio della Fm è il doppio di quello di Fr allora è sufficiente una Fm di
intensità pari alla metà di Fr per mantenere l’equilibrio .
-- Esempio 2 ----------------------------------------------------------------------------------------------------------Fm = ?
Fr = 1000 N
1,2 m
2,4 m
Supponiamo di risolvere l’esercizio come in precedenza ma avendo
spostato il fulcro nella posizione indicata in figura, ovvero in modo che
il braccio di Fm rispetto al fulcro valga bm = 1,20 m mentre quello della
Fr valga br = 2,40 m
Si ottiene :
Fm = 1000* 2,4/1,2 = 2000 N (!!!!)
R
Per equilibrare un carico di 1000 N risulta necessaria una forza motrice
di ben 2000 N .
La leva in questo caso non amplifica , bensì riduce l’effetto della forza motrice ; in questo caso la leva
viene definita “Svantaggiosa” .
Notiamo che siccome il braccio della Fm è la metà di quello di Fr allora è necessaria una Fm di intensità
pari al doppio di Fr per mantenere l’equilibrio .
-- Esempio 3 ----------------------------------------------------------------------------------------------------------Fm = ?
1,8 m
Fr = 1000 N
1,8 m
Supponiamo di risolvere l’esercizio come in precedenza ma avendo
spostato il fulcro esattamente a metà della leva come indicato in figura,
ovvero in modo che sia il braccio di Fm che quello di Fr rispetto al
fulcro valgano b = 1,80 m
Si ottiene :
Fm = 1000* 1,8/1,8 = 1000 N
R
Per equilibrare un carico di 1000 N risulta necessaria una forza motrice
di 1000 N , esattamente pari a quella che sarebbe necessaria per tenere sollevato il carico direttamente con
le proprie braccia .
La leva in questo caso non amplifica né riduce l’effetto della forza motrice ma la trasmette esattamente
identica all’altra estremità ; in questo caso la leva viene definita “Indifferente” .
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 11
Notiamo che siccome il braccio della Fm è uguale a quello di Fr allora è necessaria una Fm di intensità
esattamente uguale a quella di Fr per mantenere l’equilibrio .
In questo caso un piccolo vantaggio pratico consiste nel fatto che , essendo la Fm rivolta verso il basso, è
possibile, per una persona, sfruttare il proprio peso.
-- Esempio 4 ----------------------------------------------------------------------------------------------------------Fr = 1000 N
Fm = ?
3,0 m
Risolviamo ora l’esercizio dell’esempio 1 avendo spostato il fulcro
come indicato in figura, ovvero in modo che il braccio di Fm rispetto al
fulcro valga bm = 3,00 m mentre quello della Fr valga br = 0,60 m
Si ottiene :
0,6
Fm = 1000* 0,6/3,0 = 200 N (!!)
R
Notiamo che siccome il braccio della Fm rispetto al fulcro è cinque volte
maggiore di quello della Fr allora è sufficiente una Fm di intensità pari ad 1/5 di Fr per mantenere
l’equilibrio ( ………… si fa sempre meno fatica) .
----------------------------------------------------------------------------------------------------------------------------Da quanto esposto nelle righe precedenti risulta evidente che aumentando parecchio
il valore del braccio della forza motrice rispetto a quello della forza resistente si
possono equilibrare teoricamente forze sempre più grandi (a patto che la leva ed il
suo fulcro siano in grado di resistere).
Tutto questo giustifica la famosissima frase attribuita ad Archimede , il grande genio,
matematico, ingegnere, fisico e inventore vissuto a Siracusa ( 287 a.C. – 212 a.C.),
uno dei massimi scienziati della storia :
“Datemi una leva ed un punto di appoggio e vi solleverò il mondo”
In sostanza per stabilire se una leva è vantaggiosa o meno è sufficiente confrontare i valori del braccio di
Fm e di quello di Fr rispetto al fulcro. La questione può essere riassunta nello schema seguente :
m >r
Fm = Fr . r
m
m =r
m <r
r
<1
m
Fm < Fr
r
=1
m
Fm = Fr
r
>1
m
Fm > Fr
Vantaggiosa
Fr
Fm
m
Indifferente
Fm
Fr
m
Svantaggiosa
r
r
Fr
Fm
m
r
Nella tecnica si è a volte costretti a ricorrere all’utilizzo di leve svantaggiose che però consentono di
ottenere movimenti utili.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 12
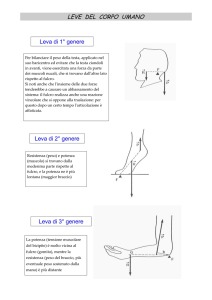
Dal punto di vista geometrico invece, in base alla posizione relativa di Forza Motrice, Forza Resistente e
Fulcro le leve possono essere distinte in tre generi :
Fr
Fm
m
1° GENERE
Il Fulcro si trova tra la forza resistente e la forza motrice
Può essere Vantaggiosa , Svantaggiosa o Indifferente
a seconda della posizione del fulcro.
2° GENERE
Il Fulcro è esterno alle due forze , dalla parte della forza resistente.
E' sempre Vantaggiosa in quanto il braccio della forza motrice è
sempre maggiore di quello della forza resistente.
3° GENERE
Il Fulcro è esterno alle due forze , dalla parte della forza motrice.
E' sempre Svantaggiosa in quanto il braccio della forza motrice è
sempre minore di quello della forza resistente.
r
Fr
Fm
r
m
Fr
Fm
m
r
-- Esempi ----------------------------------------------------------------------------------------------------------LE FORBICI
Fr
Fm Si tratta di due leve di 1° genere accoppiate.
La forza motrice è data dalla spinta delle dira mentre la forza resistente è
fornita dalla reazione elastica del corpo da tagliare.
Può essere vantaggiosa o svantaggiosa a seconda della posizione in cui si
trova il corpo da tagliare.
fulcro
----------------------------------------------------------------------------------------------------------------------------Fr
Fm
br
bm
LA CARRIOLA
E’ una leva di secondo genere e come tale sempre vantaggiosa per
quanto riguarda il sollevamento dei carichi.
Per lo spostamento in orizzontale naturalmente entrano in gioco altre
forze .
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 13
Fr
Fm
LO SCHIACCIANOCI E LE PINZE
E’ costituito dall’insieme di due leve di secondo genere, quindi vantaggiose.
La forza resistente è costituita dalla reazione elastica del corpo da
schiacciare.
Le pinze funzionano in modo analogo.
fulcro
----------------------------------------------------------------------------------------------------------------------------L’AVAMBRACCIO UMANO
Per quanto riguarda il sollevamento di oggetti pesanti l’avambraccio si
comporta come una leva di terzo genere e come tale svantaggiosa.
La forza motrice viene trasmessa alle ossa dell’avambraccio dai tendini
tesi per la contrazione muscolare del bicipite brachiale .
Il fulcro è costituito dall’articolazione del gomito.
Fr
Il braccio della forza motrice è molto inferiore a quello della forza
Fm
resistente (peso del corpo posato sulla mano).
Questo svantaggio statico è però controbilanciato dalla notevole
snellezza, versatilità e capacità di movimento dell’arto.
----------------------------------------------------------------------------------------------------------------------------L’ APRIBOTTIGLIA
m
r
Esistono diversi tipi di apribottiglia, ma in genere possono essere
Fm
considerati sempre leve di 1° genere vantaggiose in quanto, come in
figura il braccio della forza motrice è maggiore di quello della forze
Fulcro
resistente, data dalla resistenza per attrito del tappo sul collo della
Fr
bottiglia.
----------------------------------------------------------------------------------------------------------------------------IL PIEDE DI PORCO
Fm
Si tratta di una leva di 1° genere molto vantaggiosa.
Il braccio della forza motrice è molto maggiore di quello della forza
resistente, per cui consente di sollevare carichi anche molto pesanti.
Per questo motivo deve avere una elevata resistenza alla flessione.
Ci vuole però un grande spostamento dell’estremità cui è applicata
la forza motrice per produrre un piccolo sollevamento del carico.
Fr
Fulcro
----------------------------------------------------------------------------------------------------------------------------LA LEVA DEL FRENO
m
Fm
Fulcro
r
Fr
Si tratta di una leva di 1° genere vantaggiosa
caratterizzata da una forma particolare .
Il braccio della forza motrice , data dalle dita della
mano, è maggiore di quello della forza resistente, data
dalla resistenza del filo che aziona il freno.
Il fulcro è il perno che collega la leva al manubrio.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 14
FORZE PARALLELE CONCORDI
Il metodo grafico visto in precedenza per la costruzione della risultante di forze applicate ad un corpo
rigido, in alcuni casi particolari ma importanti non è applicabile.
Esaminiamo il caso in cui ad un corpo rigido siano applicate due forza parallele concordi (con la stessa
direzione e lo steso verso) come quelle indicate in figura.
In questo caso non è possibile far scorrere i vettori lungo la loro retta d’azione fino al punto di incontro in
quanto due rette parallele non si incontrano mai.
Tralasciando la dimostrazione analitica di quanto segue possiamo fare alcune considerazioni :
1- la risultante avrà certamente la stessa direzione e lo stesso verso delle
due componenti (parallela ad F1 ed F2)
F1
F2
2- la risultante dovrà avere modulo pari alla somma delle due componenti
in quanto hanno stessa direzione e stesso verso, quindi :
R = F1+F2
3- per avere lo stesso effetto delle due componenti agenti
contemporaneamente la risultante dovrà essere più vicina alla forza di
maggiore intensità
Rimane indeterminata la posizione della risultante.
E’ stata però messa a punto una costruzione grafica con cui si può determinare la posizione di un punto
per il quale passa la risultante.
------------------------------------------------------------------------------Costruzione grafica del punto di applicazione della risultante di
forze parallele concordi
-------------------------------------------------------------------------------
R = F1+F2
F1
1- Si prende un segmento lungo come F1 , lo si trasla dalla parte
opposta e lo si ribalta (segmento BD)
C
F2
P
2- Si prende un segmento lungo come F2 , lo si trasla dalla parte
opposta e … basta (segmento AC)
A
B
d1
d2
3- Il punto di incontro tra il segmento AB congiungente i punti di
applicazione delle due forze ed il segmento CD è un punto per cui
passa la risultante (punto P).
D
Una volta individuata la posizione della risultante sarà possibile rappresentarla con un vettore ; potremo
disegnare il vettore risultante parallelo ai due componenti, con lo stesso verso e di lunghezza pari alla
somma di F1 ed F2, con origine nel punto P appena individuato.
Come previsto il vettore risultante è posizionato più vicino alla forza maggiore, in questo caso la F1.
La risultante è sempre interna alle due componenti e più vicina alla forza maggiore
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 15
Poiché la Risultante ed il sistema costituito dalle due forze F1 ed F2 parallele, concordi, agenti
contemporaneamente devono essere equivalenti dovranno produrre lo stesso valore del momento rispetto a
qualsiasi punto del piano.
Possiamo allora concludere che siccome il momento della risultante rispetto al punto P vale zero (il
braccio è nullo) , dovrà essere nullo anche il momento risultante delle due forze componenti, ovvero :
- F1 * d1
+
F2 * d2 = 0
F2 * d2 = F1 * d1
F1 d2
=
F2
d1
Le distanze d1 e d2 della risultante dalle forze F1 ed F2 sono
inversamente proporzionali al modulo delle forze stesse
Inoltre evidentemente si avrà che :
b = d1 + d2
-- Esempio ----------------------------------------------------------------------------------------------------------Un SUV sta percorrendo un tratto fuoristrada a mezza costa caratterizzato da pendenza trasversale.
Esaminiamo le condizioni di sicurezza nei confronti del ribaltamento trasversale.
Sicurezza
Condizione Limite
Fp
Fp
Fp
Mris(A) = 0
A
R1
Ribaltamento
Mris(A) = 0
R1=0
Mris(A) = - Fp*b
A
A
R2
R = - Fp
Con bassa pendenza trasversale Le
reazioni del terreno al di sotto delle
ruote costituiscono una coppia di forze
parallele concordi con quella di valle di
intensità maggiore.
La risultante delle due reazioni diventa
esattamente uguale e contraria al peso
del veicolo (applicato nel baricentro)
garantendo l'equilibrio.
Il momento risultante delle forze rispetto
al punto A vale zero ed il veicolo non
ruota attorno a tale punto.
b
R = - Fp
R = R2 = - Fp
Aumentando la pendenza trasversale si
ha una diminuzione della forza R1 ed un
aumento della R2 di valle . Nella
condizione limite la R1 diventa nulla e la
reazione R2 diventa esattamente uguale
e contraria al peso del veicolo.
Teoricamente l'equilibrio è ancora
possibile in quanto la risultante delle
forze agenti è nulla così come è nullo il
momento risultante rispetto al punto A,
ma in pratica si tratta di una situazione
pericolosissima (basta una piccola
irregolarità del terreno per produrre il
ribaltamento).
Superata la posizione limite non ci può
più essere equilibrio .
La risultante delle reazioni del terreno
può essere solamente interna alle due
forze o al limite coincidere con una delle
due (nel nostro caso quella di valle) e
non può più avere la medesima retta
d'azione della forza peso.
La Fp produce rispetto al punto A un
momento ribaltante (-) che non può
essere annullato dalle altre forze per cui
si ha il ribaltamento.
Il ribaltamento avviene quando la verticale per il baricentro del veicolo esce dal perimetro della ruote.
Per quanto riguarda il ribaltamento trasversale si ha maggiore sicurezza quando il baricentro è più basso
possibile ed in generale con veicoli “ larghi e bassi” ; naturalmente esistono limiti pratici legati alla
irregolarità del terreno (altezza da terra) ed alla possibilità di
superare passaggi stretti ed accidentati (larghezza del veicolo) nel fuoristrada.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 16
Il BARICENTRO
E’ noto che tutti i corpi vengono attirati dalla Terra verso il suo centro con una forza
che chiamiamo “Forza di gravità” o “Peso”.
Di solito si rappresenta questa forza con un vettore , con la “direzione del filo a
piombo”, che ha un punto di applicazione ben definito chiamato “Baricentro” .
Cerchiamo ora di approfondire il discorso.
Innanzitutto si deve considerare che un corpo è costituito da un numero elevatissimo
Peso
dell'oggetto
di particelle, ciascuna delle quali possiede un proprio peso.
Il Peso non è quindi una forza concentrata in un punto, ma è distribuita su tutto il
corpo (vedi schema a fianco).
Quella che comunemente indichiamo come Forza di Gravità o Peso del corpo non è altro che la risultante
di tutte queste forze parallele e concordi. Il punto di applicazione questa risultante è il Baricentro.
Vediamo come è possibile individuare questo punto, almeno in alcuni casi semplici.
Corpi Omogenei = Corpi che presentano una densità e quindi un peso specifico costanti .
Ogni piccola porzione del corpo presenta sempre la stessa densità.
Corpi Non Omogenei =
Corpi che presentano parti caratterizzate da densità differenti. Ad esempio un
martello con la testa di ferro ed il manico di legno è un corpo non omogeneo .
Prendiamo in esame un oggetto di forma semplice e simmetrica come una piastra metallica
rettangolare omogenea di spessore costante.
FIG. 1
FIG. 3
FIG. 2
G
F' F' F' F'
G
F1
F
F
F
F
2F
F
F
2F
2F
R = 6F
Suddividiamo il corpo omogeneo in striscie uguali
tra loro, ognuna delle quali avrà un peso.
Naturalmente la suddivisione dovrebbe essere
molto più fitta di quella in figura per
rappresentare correttamente la realtà .
Si tratta di un insieme di forze parallele concordi
ed uguali tra loro. Cerchiamo di determinarne la
risultante con i metodi visti in precedenza .
La risultante delle due forze di estermità (nere)
cadrà esattamente a metà della loro distanza,
cioè sull'asse di simmetria dell'oggetto.
Anche la risultante delle due forze blu cadrà a
metà della loro distanza ovvero nel centro del
corpo, e così si può dire della risultante delle due
forza verdi.
Queste tre risultanti si sommeranno per formare il
vettore che rappresenta il peso complessivo del
corpo passante per un punto , che indicheremo
con G , segnando la sua posizione con un
segmento color magenta.
F2
F3
2F1
2F'
2F2
2F'
2F3
R = 4F' = 6F
Ruotiamo ora il corpo di 90° come in
figura 2.
Ripetiamo l'operazione precedente
suddividendo il corpo in striscie uguali fra
loro e simmetriche e determiniamone la
risultante.
Come nel caso precedente le singole
forze parallele si sommano per formare
la risultante che è il peso del corpo
passante per l'asse di simmetria.
Naturalmente il valore di questa
risultante sarà identico a quello
precedente, trattandosi del peso
complessivo dell'oggetto, che è sempre
lo stesso.
Segnamo la posizione della risultante
con un altro segmentino color magenta.
I due segmenti si incrociano in un punto
che chiameremo G .
F1
F3
F2
R = 2F1 + 2F2 + 2F3 =
= 4F' = 6F
Ruotiamo ora il corpo di un angolo qualsiasi
(diverso da 90° e dai suoi multipli).
Suddividiamo l'oggetto in striscie. Questa
volta le striscie non saranno tutte uguali ed
ognuna avrà il proprio peso.
La risultante delle due forze di estermità
(nere) cadrà esattamente a metà della loro
distanza.
Anche la risultante delle due forze blu cadrà a
metà della loro distanza ovvero sulla stessa
retta su cui giace la risultante delle prime due.
Lo stesso discorso vale per la risultante delle
due forze verdi.
Queste tre risultanti si sommeranno per
formare il vettore che rappresenta il peso
complessivo del corpo .
Si può verificare che il vettore risultante
passa sempre per il punto G determinato
precedentemente.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 17
In generale si può verificare che la risultante delle forze distribuite parallele e concordi passa sempre per lo
stesso punto, indipendentemente dalla posizione in cui l'oggetto viene posto e dal tipo di suddivisione
operata.
A questo punto, indicato con la lettera G (da gravità) si attribuisce il nome di Baricentro o Centro di Gravità.
Il Baricentro viene spesso indicato come Centro delle Forze parallele che rappresentano l'azione della
gravità sui corpi.
Il peso di un corpo viene di solito rappresentato come una forza singola concentrata in un punto perché si fa
implicitamente riferimento alla risultante di tutte le forze parallele che costituiscono il peso dell'oggetto .
E’ abbastanza semplice constatare, riflettendo sull’esempio precedente, che il Baricentro si trova sempre
sugli assi di simmetria.
Nel caso precedente , data la presenza di due assi di simmetria , l’unico punto che appartiene ad entrambi è
proprio il punto di intersezione tra i due assi.
Esaminiamo ora il caso di un corpo omogeneo che non presenta però assi di simmetria come
una piastra metallica di spessore costante simile a quella della figura a fianco.
FIG. 1
FIG. 2
FIG. 3
d
2d/3 d/3
G
F
F
2F 2F
F
F
2F 2F
2F
2F
4F
4F
R = 6F
Pensiamo di suddividere il corpo in 4 striscie uguali a due a due . La risultante delle prime due forze (blu) varrà 2F e sarà
posizionata esattamente al centro dei due vettori.
La risultante della seconda coppia di forze (verdi) varrà 4F e sarà posizionata al centro di questi due vettori.
Ci siamo così ridotti a due forze parallele concordi di intensità differente; in particolare, in questo caso, una doppia
dell'altra.
Come sappiamo la risultante di queste due forze varrà 6F e sarà interna ai due vettori, ma più vicina alla forza di maggiore
intensità.
Inoltre siccome le distanze d1 e d2 delle forze dalla risultante sono inversamente proporzionali al modulo delle forze
stesse, la nostra risultante si troverà ad una distanza dalla forza minore doppia rispetto alla distanza dalla forza maggiore
Come risulta evidente il Baricentro in questo caso non cade al centro dell'oggetto, ma è spostato verso la parte
caratterizzata da maggior massa.
Lo stesso metodo potrebbe essere utilizzato ruotando il corpo di 90° ottenendo un risultato analogo, col baricentro spostato
dalla parte in cui è presente maggior massa.
Esaminiamo ora il caso di una piastra rettangolare di spessore costante, che presenta
quindi due assi di simmetria geometrici ma non omogenea perché costituita per metà da
un materiale e per l’altra metà da un materiale di densità doppia.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 18
FIG. 1
FIG. 2
FIG. 3
d
2d/3
d/3
G
F
F
F
2F
2F
F
2F
2F
2F
2F
4F
4F
R = 6F
Pensiamo di suddividere il corpo in 4 striscie geometricamente uguali che però avranno peso diverso. La risultante delle
prime due forze (blu) varrà 2F e sarà posizionata esattamente al centro dei due vettori.
La risultante della seconda coppia di forze (verdi) varrà 4F e sarà posizionata al centro di questi due vettori.
Ci siamo così ridotti a due forze parallele concordi di intensità differente; in particolare, in questo caso, una doppia
dell'altra.
La risultante di queste due forze sarà interna ai due vettori, ma più vicina alla forza di maggiore intensità.
Inoltre siccome le distanze d1 e d2 delle forze dalla risultante sono inversamente proporzionali al modulo delle forze
stesse, la nostra risultante si troverà ad una distanza dalla forza minore doppia rispetto alla distanza dalla forza maggiore.
Il Baricentro in questo caso non cade al centro dell'oggetto, ma è spostato verso la parte caratterizzata da maggior densità
e quindi maggior peso.
L'oggetto esaminato presenta una simmetria sia dal punto di vista geometrico che da quello della densità rispetto ad un
asse orizzontale (indicato in figura) , per cui il baricentro si troverà su questo asse .
Esaminiamo infine una cornice rettangolare, omogenea, di spessore costante, che presenta quindi due assi di
simmetria .
FIG. 2
FIG. 1
FIG. 3
F2
G
G
F1
F1
F2
R = 2F1 + 2F2
Possiamo pensare di suddividere la cornice in 4 rettangoli come in figura.
E' evidente che la risultante di queste forze parallele sarà posizionata esattamente al centro della cornice; questo
ragionamento può essere ripetuto anche ruotando l'oggetto di 90°
In conclusione possiamo affermare che il baricentro dovrà trovarsi esattamente nel punto centrale della cornice.
Questo è confermato anche dal fatto che il nostro oggetto presenta due assi di simmetria e, come abbiamo già visto, il
baricentro si posiziona sempre sugli assi di simmetria.
L'unico punto che si trova su entrambi gli assi è il centro della cornice.
In questo caso possiamo osservare che il baricentro cade esternamente al corpo, cioè in un punto in cui non c'è
materia.
Ricordiamo che a risultante di un sistema di un sistema di forze è una unica forza ideale (non reale) che da sola
sarebbe in grado di produrre gli stessi effetti delle forze componenti agenti contemporaneamente.
Nel nostro caso possiamo quindi concludere che la cornice, sotto l'azione della gravità, si comporterà come se su di lei
fosse applicata una unica forza (uguale al peso complessivo) applicata nel punto G , pensando che esso sia in
qualche modo rigidamente collegato al corpo.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 19
Riassumendo :
-
Il Baricentro è il punto in cui si può pensare applicata la risultante delle forze parallele concordi che
costituiscono il peso del corpo indipendentemente dalla sua posizione ed orientazione nello spazio.
Il Baricentro sta sempre sugli assi di simmetria (se esistono)
Il Baricentro è sempre spostato dalla parte del corpo in cui c’è più massa quindi più peso
Il Baricentro può anche essere un punto al di fuori del corpo
Il Baricentro di un corpo che può modificare la propria forma può cambiare posizione.
-- Esempi ----------------------------------------------------------------------------------------------------------C
G
G
G
AC/3
G
B
A
AB/3
Cerchio
Rettangolo
Triangolo equilatero
Triangolo rettangolo
Ha infiniti assi di simmetria
Il Baricentro coincide col
centro
Ha due assi di simmetria
Il Baricentro coincide col
punto di incontro degli assi di
simmetria e delle diagonali
Ha tre assi di simmetria (altezze)
Il Baricentro coincide col punto di
incontro degli assi di simmetria
che sono anche altezze ,
mediane e bisettrici
Il Baricentro si trova sull rette
parallele ai cateti distanti dal
vertice corrispondente all'angolo
retto di 1/3 della lunghezza dei
cateti stessi.
Il BARICENTRO E LA QUALITA’ DELL’EQUILIBRIO
Tra tutte le posizioni di equilibrio di un corpo, ovvero le posizioni in cui teoricamente è “fermo” ci sono
differenze sostanziali. Alcune posizioni possono facilmente essere realizzate e mantenute, altre sono
difficilissime da realizzare e pressochè impossibili da mantenere nel tempo.
Vediamo subito un semplice esempio in cui una pallina è appoggiata su una semisfera disposta in modo
diverso e poi viene appoggiata sul tavolo piano.
Tutte e tre le posizioni rappresentate nella figura seguente sono di equilibrio, ovvero posizioni in cui la
pallina sta teoricamente ferma, ma ci sono notevoli ed importanti differenze tra una e l’altra.
B
A
A
= posizione di EQUILIBRIO STABILE
A seguito di qualsiasi piccolo
spostamento dalla posizione di
equilibrio la forza agente (in questo
caso il peso ) tende a riportare la
pallina nella posizione di partenza.
C
B
= posizione di EQUILIBRIO INSTABILE
A seguito di qualsiasi piccolissimo
spostamento da quella che
teoricamente è una posizione di
equilibrio la forza agente (in questo
caso il peso ) tende ad allontanare la
pallina dalla posizione di partenza.
C
= posizione di EQUILIBRIO INDIFFERENTE
A seguito di qualsiasi piccolo
spostamento dalla posizione di equilibrio
la forza agente (in questo caso il peso )
non produce nessun effetto sulla pallina
e la lascia nella nuova posizione
anch'essa di equilibrio.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 20
Le posizioni di tipo B sono posizioni in cui l’equilibrio è teoricamente possibile, ma nella realtà risulta
difficilissimo se non impossibile riuscire a realizzarle e mantenerle.
Per questo motivo in campo tecnologico non vengono
di solito utilizzate le posizioni di equilibrio instabile
cercando invece quelle di equilibrio stabile, molto più
R = - Fp
R = - Fp
R = - Fp
semplici da ottenere e mantenere, quindi più sicure.
Le cabine delle funivie, ad esempio, sono appese ai
cavi in acciaio e si trovano in una posizione di
equilibrio stabile.
Se , per effetto del vento o di spostamenti interni delle
persone trasportate la cabina oscilla, la forza peso
tende sempre a riportarla nella posizione ottimale in
Fp
Fp
cui il baricentro si trova sulla verticale passante per i
Fp
cavi ; in questo modo infatti il peso e la reazione
elastica dei cavi si annullano mentre è nullo anche il
momento visto che il braccio della coppia di forze diventa zero.
Fp
Fp
M=0
M≠0
R = - Fp
R = - Fp
Un equlibrista che cammina sulla corda tesa si trova in posizione di equilibrio instabile.
E’ una posizione che può essere mantenuta solamente con continui e rapidi spostamenti del corpo e/o del
bilancere col quale alcuni funamboli si aiutano.
L’abilità dell’equilibrista sta proprio nel mantenere il baricentro sulla verticale che passa per la corda in
modo che la reazione elastica di quest’ultima sia esattamente uguale e contraria al peso ed il momento
risultante sia nullo; solo in queste condizioni l’atleta non ruota attorno alla fune e quindi non cade.
In conseguenza di uno sbilanciamento, anche molto leggero, il peso e la reazione elastica della fune vengono
a formare una coppia di forze con momento diverso da zero che tende a far cadere l’equilibrista.
Nel caso dei corpi vincolati su cui agisce la forza di gravità si può affermare che l’equilibrio sarà
stabile nel caso in cui il baricentro si trovi sulla verticale passante per il vincolo ma al di sotto di
esso ; instabile in caso contrario, ovvero quando il baricentro è al di sopra del vincolo.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 21
FORZE PARALLELE DISCORDI
F1
Esaminiamo il caso in cui ad un corpo rigido siano applicate due
forze parallele discordi (con la stessa direzione e verso opposto)
come quelle indicate in figura.
Anche in questo caso non è possibile far scorrere i vettori lungo la
loro retta d’azione fino al punto di incontro in quanto due rette
parallele non si incontrano mai.
Possiamo, anche in questo caso, fare alcune considerazioni :
F2
------------------------------------------------------------------------------Costruzione grafica del punto di applicazione della risultante
di forze parallele discordi
-------------------------------------------------------------------------------1- la risultante avrà certamente la stessa direzione delle
due componenti (parallela ad F1 ed F2)
F1
2- la risultante avrà certamente il verso della forza maggiore
(quello di F1 nel caso in figura)
R = F1-F2
A
P
B
F2
D
3- la risultante dovrà avere modulo pari alla differenza tra i
valori delle due componenti in quanto hanno stessa
direzione ma verso opposto, quindi :
R = F1-F2
C
d1
d2
La risultante è sempre esterna alle due componenti e posizionata dalla parte della forza maggiore
Anche in questo caso, partendo dall’equivalenza tra la risultante ed il sistema
costituito dalle due forze F1 ed F2 discordi si ottiene la relazione :
Naturalmente si dovrà tenere conto delle corrette distanze d1 e d2 delle due forze
dalla risultante
(vedere figura precedente) per cui si avrà :
F1 d2
=
F2
d1
b = d2 – d1
LA COPPIA DI FORZE
Si tratta di un caso particolare, ma molto importante, di forze
parallele discordi.
F
F
Si intende per “Coppia di Forze”, o semplicemente “Coppia”,
un sistema costituito da due forze parallele, discordi e di
uguale intensità.
b
b
braccio della
coppia
braccio della
coppia
F
F
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 22
b = Braccio della Coppia
Distanza tra le rette d’azione delle forze .
Deve essere misurato sulla perpendicolare alle rette d’azione delle forze
L’effetto più evidente di una coppia di forze applicata ad un corpo rigido è quello di provocarne la rotazione.
Nella nostra esperienza quotidiana veniamo spesso a contatto con coppie di forze che determinano rotazione
dei corpi su cui vengono applicate.
F
F
F
b
b
F
F
b
b
F
F
F
Chiave di casa
Volante
Chiave a croce per
cambio pneumatici
Cacciavite
Questo sistema di forze presenta caratteristiche veramente particolari ed “inaspettate”.
Alla luce di quanto fatto in precedenza potremmo infatti affermare che , essendo uguali i moduli delle due
forze (F1=F2=F), allora la risultante dovrebbe essere nulla in quanto tale è la differenza tra le due
componenti :
FR = F1 – F2 = F – F = 0 (!?)
Questa conclusione appare immediatamente non accettabile in quanto porterebbe a concludere che le due
forze parallele discordi applicate ad un corpo rigido dovrebbero essere equivalenti alla assenza di forze
(risultante nulla), mentre pare evidente che un corpo rigido sottoposto a tali azioni non può stare fermo
(come in assenza di forze).
Provando poi ad eseguire la costruzione grafica descritta in precedenza per le forze
parallele discordi ci troviamo di fronte ad altre “stranezze” , ovvero :
F1
F2
-
La risultante dovrebbe essere esterna, dalla parte della forza maggiore, ma qui
non c’è una forza maggiore dell’altra.
Le due linee non si incontrano mai
Non si riesce a determinare un punto per cui passa la risultante
In effetti dallo studio approfondito di questo sistema di forze si può concludere che :
1- Non esiste la risultante
Ovvero non esiste una forza che , da sola, possa produrre lo stesso effetto di
due forze parallele uguali ed opposte applicate in punti differenti di un corpo
rigido
2- Una coppia di forze produce solamente la rotazione del corpo rigido su se stesso senza provocare una
traslazione ( spostamento)
in effetti si capisce come una unica forza non possa avere lo stesso effetto, in
quanto può produrre una traslazione o una traslazione associata ad una
rotazione, ma mai la sola rotazione del corpo su se stesso in assenza di altre
forze o vincoli.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 23
3- Una coppia di forze produce solamente un momento che ha lo stesso valore rispetto a qualunque punto
del piano
Vediamo come si può calcolare il valore di questo momento .
In mancanza di un punto fisso, che possa fungere da fulcro, proviamo a
F
calcolare il valore del momento risultante rispetto a diversi punti del
D
piano , ovvero B, C, D .
M(B) = - F*b + F*0 = - F*b
C
B
A
M(C) = - F*b/2 + F*b/2 = - F*b
b/2
b/2
F
b
M(D) = - F*(b + a) + F*a =
= - F*b – F*a + F*a = - F*b
a
Come abbiamo verificato il valore del momento risultante, calcolato rispetto a tre i punti diversi del piano,
assume sempre lo stesso valore.
Questo fatto si verifica solamente per le coppie di forze.
Per qualsiasi altro sistema di forze agenti sul corpo rigido avremmo ottenuto valori differenti del momento
risultante.
Possiamo quindi confermare che :
il momento prodotto da una coppia di forze assume il medesimo valore per qualunque punto del piano e si
calcola facendo il prodotto tra il valore di una forza ed il braccio della coppia; il segno è legato alla
rotazione antioraria o oraria provocata secondo la convenzione precedentemente adottata per il verso dei
momenti.
F
F
M = F* b
( N*m)
Segno Negativo
(M. Orario)
b
b
-
Segno Positivo
(M. Antiorario)
+
F
F
Coppie di Forze equivalenti
Sono Coppie differenti, ma caratterizzate dallo stesso valore del Momento.
Un determinato valore del Momento può essere ottenuto in diversi modi, utilizzando coppie caratterizzate
da diversi valori di forza e braccio , come nell’esempio della figura seguente.
F1= 210 N
F2 = 105
F2 = 70
b2 = 0,8 m
b1= 0,4 m
F2 = 105
b3 = 1,2 m
F3 = 70
F1= 210 N
M1 = F1*b1 = 210*0,4 = 84 Nm
M2 = F2*b2 = 105*0,8 = 84 Nm
M3 = F3*b3 = 70*1,2 = 84 Nm
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 24
Nella pratica, quando siamo noi a dover esercitare le forze parallele , risulta conveniente utilizzare bracci il
più grandi possibile, compatibilmente con le esigenze pratiche, al fine di ridurre lo sforzo necessario a
produrre il momento e quindi la rotazione voluta.
-- Esempio 1 ----------------------------------------------------------------------------------------------------------Un cacciavite viene fatto ruotare attorno al proprio asse
longitudinale tramite una coppia costituita dalle forze di attrito
F
F
della mano sul manico aventi un braccio che coincide con il
b1
diametro del manico stesso.
b2
E’ noto che un cacciavite col manico grande permette di svitare
F
F
o avvitare più facilmente anche nel caso risulti necessario un
M2 = F*b2 > M1
M1 = F*b1
momento piuttosto elevato ; infatti, fissato il valore massimo
delle forze di attrito, avere un grande diametro del manico
permette di produrre , a parità di forza, un momento M = F*b di valore maggiore.
Sfruttando questa caratteristica inoltre si possono per esempio svitare le stesse viti con minore sforzo rispetto
ad un cacciavite col manico piccolo ( a parità di momento prodotto le forze necessarie risultano minori).
Le dimensioni del manico ovviamente sono però legate a quella della mano ed all’uso che ne deve essere
fatto, per cui non possono superare determinati limiti pratici, anche se ciò sarebbe conveniente.
Un discorso analogo può essere fatto per le chiavi a croce o per il volante di cui alla figura precedente.
E’ noto che il volante dei mezzi pesanti, come autocarri o pullman ha un diametro nettamente superiore a
quello di una automobile ; questo per consentire di poter sterzare con uno sforzo limitato, data la lunghezza
del braccio della coppia applicata (oggi sono comunemente presenti altri dispositivi come il servosterzo in
grado di aiutare notevolmente il guidatore e ridurre moltissimo l’entità delle forze da applicare al volante).
-- Esempio 2 ----- LA COPPIA MOTRICE -----------------------------------------------------------Sui libretti dei ciclomotori o delle
automobili troviamo, tra le voci più
importanti indicate, oltre al valore della
potenza massima anche quello della Coppia
Massima.
Si tratta del valore del Momento che ,
tramite il sistema Biella-Manovella-Pistone
viene trasmesso all’albero motore ed è
indicativo della accelerazione massima che
può essere ottenuta.
Normalmente viene indicato il valore
massimo, ma spesso nelle schede tecniche
dei motori è riportato anche il diagramma di
coppia che mostra l’andamento del valore di
questo momento (misurato in Nm o in Kgm)
al variare del regime di rotazione.
M (Nm)
F
F
Un grafico “piatto” è indicativo di un motore in grado di accelerare in modo efficiente su un ampio regime
di giri di rotazione quindi più “elastico”.
Un diagramma molto “appuntito” indica un motore che ha un ristretto regime di giri entro il quale è in grado
di accelerare bene, mentre al di fuori di quello l’accelerazione risulta più difficoltosa.
____________________________________________________________
ITCG Cattaneo – SEZIONE I.T.I - Corso di FISICA
- prof. Massimo Manvilli 25