27/11/2014
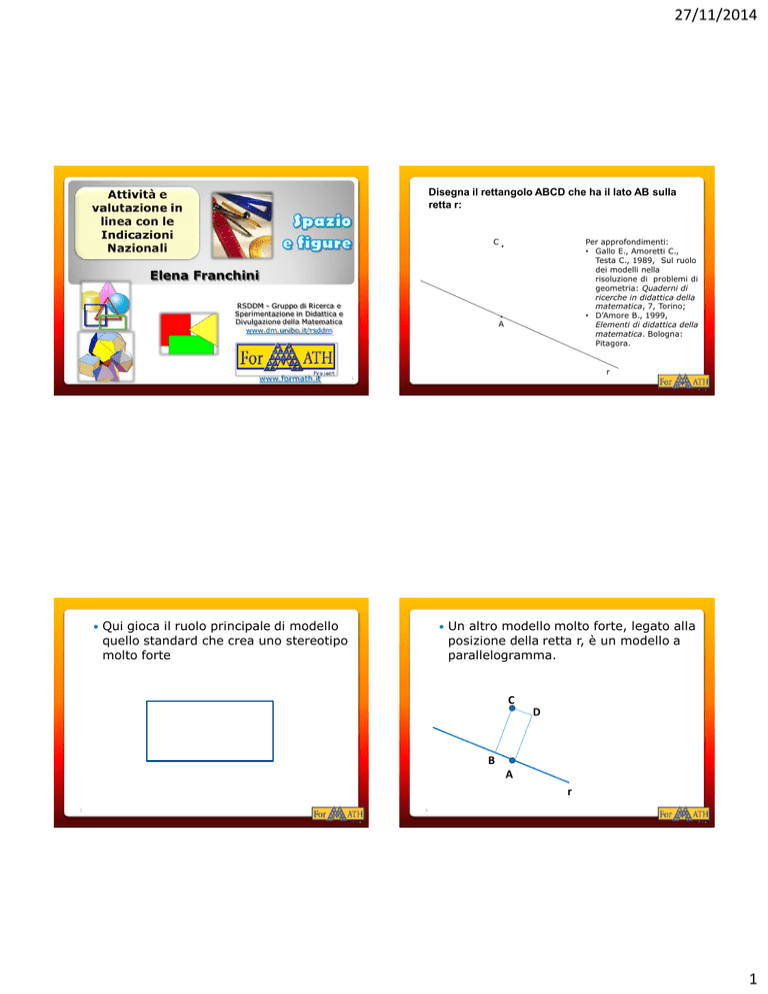
Disegna il rettangolo ABCD che ha il lato AB sulla
retta r:
C
Per approfondimenti:
• Gallo E., Amoretti C.,
Testa C., 1989, Sul ruolo
dei modelli nella
risoluzione di problemi di
geometria: Quaderni di
ricerche in didattica della
matematica, 7, Torino;
• D’Amore B., 1999,
Elementi di didattica della
matematica. Bologna:
Pitagora.
Elena Franchini
RSDDM - Gruppo di Ricerca e
Sperimentazione in Didattica e
Divulgazione della Matematica
www.dm.unibo.it/rsddm
www.formath.it
A
r
1
Qui gioca il ruolo principale di modello
quello standard che crea uno stereotipo
molto forte
Un altro modello molto forte, legato alla
posizione della retta r, è un modello a
parallelogramma.
C
D
B
A
r
3
4
1
27/11/2014
In alcuni casi gioca un ruolo notevole
anche un altro fattore: il testo che l’adulto
considera come testo unico, è visto da
alcuni studenti come una sequenza di
consegne.
C
A
◦ disegna un rettangolo
◦ chiamalo ABCD
◦ il lato AB deve stare sulla retta r
B
r
C
A
5
D
6
D
B
r
2
27/11/2014
L’alunno nel tempo costruisce un concetto riferendosi a
proprie immagini mentali.
L’immagine mentale, soprattutto all’inizio, è di carattere
figurale.
Poi entrano in azione gli altri registri semiotici: numerico,
algebrico, schematico, grafico-funzionale, topologico, ecc.
Con il passare dei giorni, dei mesi (in taluni casi anche degli
anni), se convenientemente stimolato, l’allievo perfeziona
le proprie immagini mentali:
mediante rimozione degli elementi parassiti
mediante rafforzamento degli elementi invarianti.
Esempio: costruzione del concetto di rettangolo.
11
12
All’inizio, l’immagine mentale è di carattere figurale.
Può essere indotta da un foglio di carta colorata oppure da
una figura disegnata.
Nelle prime immagini il rettangolo “appoggia” sul suo lato
maggiore:
3
27/11/2014
Nel tempo l’immagine evolve.
Per esempio il concetto di rettangolo si associa a due o più
immagini del tipo:
2
1
13
Attenzione: l’immagine figurale è forte e
contiene anche informazioni parassite.
Se un allievo ha solo l’immagine 1 di
rettangolo, non riconosce né 2 né 3 né 4
come rettangoli.
(La 1 contiene l’informazione parassita che la
dimensione maggiore è quella “orizzontale”.)
L’allievo che possiede solo le immagini 1 e 2
(quelle di gran parte dei libri di testo, che
contengono l’informazione parassita: lati
“orizzontali” e “verticali”) non riconosce né 3
né 4 come rettangolo.
14
2
1
Es: IL CUBO
L’allievo che possiede solo le immagini 1, 2, 3, 4 di
rettangolo
(che contengono l’informazione parassita “lati di lunghezza
diversa”) non riconosce né 5 né 6 come rettangolo.
A questo punto l’allievo può arricchire la propria immagine
di rettangolo giungendo a una definizione verbale: quella
di quadrilatero con gli angoli retti.
5
15
durante la Scuola Dell’Infanzia la maestra
mostra agli alunni una scatolina di legno rossa a
forma di cubo e dice agli studenti che quello è un
cubo.
Quindi un cubo è di legno? E’ rosso???
vengono mostrati altri oggetti di diverso
materiale e diverso colore a forma di cubo
Quindi non è per forza né di legno, né rosso..
È la forma che lo definisce!
4
27/11/2014
Es: IL CUBO
durante la Scuola Primaria vengono mostrati vari oggetti
a forma di cubo … dopo varie sollecitazioni e un
susseguirsi di immagini la maggior parte degli studenti
creano il modello di cubo come un solido con una data
forma.
studi rivelano che per la maggior parte degli studenti di
Scuola Primaria,
non è un
cubo!!!
conseguenza della proposta da parte
dell’insegnante di un’immagine forte e convincente di
un concetto,
che diventa persistente, confermata da continui
esempi ed esperienze;
hanno molta forza di persuasione e molta rilevanza
nelle competenze dell’allievo;
conducono ad un’accettazione immediata.
modelli che rispondono
pienamente alle sollecitazioni
intuitive e che hanno dunque
un’accettazione immediata
forte.
Efraim Fishbein
(1920-1998)
«Il livello intuitivo si riferisce alla
dinamica dell’accettazione soggettiva di
un enunciato matematico come cosa
evidente e certa»
(Fischbein , 1985)
Ma non è detto che il modello rispecchi il concetto in
questione; molte volte si tratta di modelli creatisi con
la ripetizione e niente affatto auspicati!!
«L’esistenza di incompatibilità e di
contraddizione nelle relazioni tra
il livello concettuale e il fondamento
intuitivo rappresenta una delle
principali fonti di idee sbagliate e di
errori nell’attività matematica dei
bambini» (Fischbein , 1985)
5
27/11/2014
Quando non c’è in gioco una competenza cognitiva
forte, emerge con energia il modello intuitivo. Anche
quando uno studente si è costruito un modello
corretto di un concetto, a volte, il modello intuitivo
ricompare.
«L’insistere eccessivamente nel fornire
suggerimenti intuitivi usando
rappresentazioni artificiali e troppo
elaborate può fare più male che
bene» (Fischbein , 1985)
(Van Hiele, 1984)
L’evoluzione del pensiero geometrico va ricercato a partire dalle
prime esperienze spaziali del bambino fino alle più ardite e
moderne teorie.
(Sbaragli & Mammarella, 2010)
Nei primi livelli scolastici questa disciplina è rivolta ad
organizzare l’esperienza visiva, tattile, motoria degli
allievi, puntando l’attenzione su alcune caratteristiche
spaziali degli oggetti e organizzandosi in seguito
razionalmente in modo sempre più autonomo.
Negli ultimi anni di scuola primaria e nella scuola secondaria di
primo grado dovrebbe iniziare una sistemazione e
razionalizzazione del sapere geometrico che continuerà in
modo sempre più critico e profondo nella scuola secondaria di
secondo grado e che dovrà tener conto che il valore formativo di
tale disciplina viene messo in risalto da una trattazione che
inglobi i diversi approcci possibili.
Visivo
• Riconoscere le forme presentate a livello percettivo, ma manca
l’abilità di rappresentarle mentalmente, ovvero di creare delle
immagini mentali delle forme geometriche.
• Apprendere il vocabolario geometrico, identificare e
riprodurre le figure in modo corretto.
• Si inizia a riconoscere le figure in base alle loro proprietà.
Le immagini perdono di importanza rispetto ai loro
attributi, ma le proprietà non sono ancora ordinate,.
Descrittivo- • Manca ancora l’abilità di differenziarle in termini di definizioni e
proposizioni, e di spiegare le relazioni tra le varie figure
Analitico
geometriche.
Deduzioni
informali
• Prime osservazioni delle varie relazioni tra le figure dal punto
di vista logico.
• Conoscenza di una terminologia specifica appropriata e delle
definizioni, così da poter riconoscere classi di figure e dedurne
alcune proprietà.
• Non vi è ancora una comprensione degli assiomi e delle
dimostrazioni.
6
27/11/2014
Deduttivo
Rigore
geometrico
• Si comincia ad essere in grado di distinguere
formalmente tra una proposizione e la sua inversa,
• Capire le dimostrazioni, i postulati, gli assiomi ed i
teoremi.
• Il pensiero si occupa del significato di deduzione, del
reciproco di un teorema, della condizione necessaria e
sufficiente.
• L’ultimo livello, del rigore geometrico,consente agli
studenti di apprendere la geometria non-euclidea e di
confrontare diversi sistemi di assiomi. La geometria
viene pertanto rappresentata in modo astratto.
26
28
30
7
27/11/2014
Termini ridondanti…
l’angolo
Denotazione/Denominazione
La denotazione è una frase che lo descrive, lo caratterizza
ˆ
ABC
il triangolo
la parola “retta” ha una sua denotazione: linea che può essere percorsa
senza cambiare direzione (questa non è una definizione, ma solo una
denotazione)
ABC
Non è raro trovare dizionari sui quali si denota in modo tale da
creare un circolo vizioso:
Circonferenza: curva che racchiude un cerchio;
Cerchio: parte di piano racchiusa da una circonferenza.
AB = 4 cm
32
33
Denominazione
Descrizione…
Si tratta dell’attribuzione che viene data a un nome che
serve a identificare o specificare l’oggetto o la persona o
l’ente in questione.
Retta
Punto
Poligono
Quadrato
Segmento
la descrizione mette in rilievo proprietà degli oggetti
che non saranno tutti elencati nella laconicità della
definizione
“quadrato è un rombo che
ha tutti gli angoli della
stessa ampiezza,
le diagonali della stessa
lunghezza, altri due assi di
simmetria oltre alle diagonali…”
La descrizione dunque non è la definizione;
per definire un quadrato, basta una sola di queste
proprietà, dato che da essa assunta come ipotesi si
deducono come tesi le altre.
8
27/11/2014
Definizione…
Termini primitivi
“quadrato è un rombo che ha
tutti gli angoli della stessa
ampiezza”
Una definizione serve a identificare, a circoscrivere, a
indicare, a scegliere, a designare, a denominare, a
denotare.
Vediamo bene com’è fatta una definizione.
DEFINIENDUM
è il termine
che si deve
definire
Queste parole si assumono come termini primitivi perché sono
talmente semplici e “intuitive” che non vale la pena definirle;
sono designazioni spontanee, basate su cultura precedente; si
accettano senza definizione, perché è la loro presenza nelle
circostanze descritte dagli assiomi che ne determina il
significato; si introducono come puri termini e poi la teoria
che man mano si sviluppa ne dà accezioni d’uso e/o de
finizioni implicite.
DEFINIENS
predicato
Processo
infinito???
La retta è l’insieme
infinito di punti che
hanno tutti la stessa
direzione
Dimostrazione
Ciò che assicura le verità delle asserzioni della matematica si chiama
“dimostrazione”.
Questa frase comporta che i punti dovrebbero avere di per sé
una direzione.
Il che è falso, perché una direzione deve avere dimensione 1 ed
esprimere un ordine, mentre i punti hanno dimensione 0.
Consideriamo un triangolo ABC ed i
suoi angoli interni a, b e c.
Quanto misura la somma delle
ampiezze dei tre angoli interni di
ABC?
Una “direzione” è una componente di un vettore, a parte la
lunghezza che è maggiore di zero, ma non definita
La retta, come tutti i termini
primitivi, si può solo descrivere,
denominare e designare ma NON
definire!
dobbiamo “dimostrare” e non misurare, cioè fare
un ragionamento convincente che non dipenda
dal particolare triangolo, dalla particolare
situazione, dalle misure, ma che sia generale.
39
9
27/11/2014
La geometria degli Elementi di Euclide, la più classica delle classiche,
quella che chiunque ha studiato a scuola, si basa tutta su questa
affermazione: è unica la retta che passa per P, parallela a r.
L’unicità della parallela caratterizza la geometria di Euclide; ma
non è una verità dimostrata, si tratta di un assioma. Se fosse
dimostrata, non ci sarebbe più nulla da dire, la parallela è una
e basta; ma se è un assioma, chiunque di noi lo può cambiare
come crede e, appunto, sostituirlo con altri assiomi.
40
41
(Sbaragli (2005),
Misconcezioni “inevitabili” e
misconcezioni
“evitabili”)
Esame di Matematica a Scienze della
Formazione
R.: Che cos’è un angolo?
S.: Un angolo è la lunghezza dell’arco
R.: Allora, a mano a mano che ti sposti
l’angolo diventa sempre più ampio?
S.: È vero, non ci avevo mai pensato!
42
L’“archetto” dell’angolo rappresenta una
misconcezione “evitabile” in quanto
dipende da due diverse cause:
la ripetitiva proposta della stessa
rappresentazione;
la scelta della rappresentazione stessa che
meno di altre rispetta le proprietà del
concetto che si vuole far apprendere
(l’illimitatezza dell’angolo contrasta con la
limitatezza dell’archetto).
43
10
27/11/2014
Come può essere evitata
Questa misconcezione “evitabile” potrebbe
non crearsi se si punta l’attenzione
dell’allievo sulla caratteristica più rilevante
di tale oggetto nel contesto della
matematica: la sua illimitatezza. Nel dare
risalto a tale proprietà si potrebbero
mostrare varie rappresentazioni diverse,
tenendo conto dell’importanza
dell’interazione tra gli oggetti figurali e
concettuali.
44
Lingua comune e linguaggio
matematico
Osservazione
In questo caso gioca un
ruolo negativo anche il
termine “interni”…
45
La rappresentazione “archetto” soddisfa
maggiormente il contesto di lingua
comune, piuttosto che quello
matematico…
“Metti questa penna in quell’angolo del
tavolo”: si intende la parte di piano il più
possibile vicina ad un vertice
46
In questa ottica si potrebbe rappresentare
un angolo di un poligono, proponendo la
seguente immagine, dove l’illimitatezza
dell’angolo contrasta la limitatezza del
poligono.
Quell’“archetto” sembra essere
l’esplicitazione di ciò che si intende per
angolo in lingua comune
47
11
27/11/2014
(Sbaragli (2005),
Misconcezioni “inevitabili” e
misconcezioni
“evitabili”)
Obiettivo didattico
Riuscire a far sì che gli allievi
concepiscano gli oggetti matematici
facendo prevalere i concetti sulle
immagini, in modo da sapere poi
trasferire l’aspetto concettuale su
ogni singola proposta figurale che
viene loro fornita.
48
50
Durante una sperimentazione in una
IV primaria
«Quello che hai in mano tu è un rombo…
quello che abbiamo in mano noi è un
quadrato»
49
R.: «Perché il mio è un rombo e il
vostro un quadrato?»
B.: «Perché la maestra ci ha detto che il
rombo ha le diagonali orizzontali e
verticali, mentre il quadrato ha le
diagonali oblique».
A questo punto, come è possibile
sostenere che questa immagine è davvero
un quadrato?
Va primaria
e Ia secondaria
51
12
27/11/2014
V primaria
D23_a
1,5
21,9
76,6
D23_b
5,3
53,1
41,5
Non risposte
sbagliate
Una convenzione, accettata da tutti i libri
di testo, è chiamare il seguente lato del
trapezio con il nome di lato obliquo.
corrette
D16a
2,5
19,0
78,5
D16b
8,2
46,4
45,4
I secondaria
52
53
(Sbaragli (2005),
Misconcezioni “inevitabili” e
misconcezioni
“evitabili”)
La parola base nello spazio…
Nello spazio c’è chi definisce base la faccia
sulla quale “appoggia” il solido
Un uso improprio di questi termini, basato
esclusivamente sull’importanza data alla
posizione assunta dall’oggetto, piuttosto che
alle caratteristiche matematiche dell’oggetto
stesso, potrebbe generare misconcezioni
“evitabili”.
54
55
13
27/11/2014
Durante una sperimentazione alla
scuola secondaria…
Alla sollecitazione: «Di quale poliedro si
tratta?»
P.: «Non so che cosa sia, ma se lo rigiri
diventa una piramide a base quadrata»
56
58
57
La ripetitiva proposta di rappresentazioni
stereotipate comporta che la posizione
vincola l’oggetto del quale si sta parlando.
Alcuni insegnanti affermano che la parola
base nel piano è il lato del poligono che
viene disposto orizzontalmente rispetto al
lettore e nella parte inferiore del foglio.
59
14
27/11/2014
In una V primaria… «Colora una delle basi
del seguente quadrato»
La maggioranza degli allievi fornisce le
seguenti risposte…
60
- «Questa figura non ha nessuna base, perché la base
sono i lati messi sdraiati, così:
»;
- «Questo quadrato ha come base il vertice disegnato
in basso»;
- «Questo quadrato ha come base i due lati in basso»
(rappresentati nella parte inferiore del foglio che
vengono quindi colorati dall’allievo).
61
Studenti di scuola superiore…
S.: «Il rombo non ha le basi, ha solo le
diagonali»
Unica formula dell’area conosciuta per un
rombo:
A=(d1 × d2)/2
e non la formula più intuitiva:
Lunghezza di un lato × relativa altezza
essendo un rombo un caso particolare di
parallelogrammo.
62
63
15
27/11/2014
Nell’insegnamento
della matematica
vi sono dei concetti considerati
semplici da essere appresi da parte
degli allievi ma che, in realtà, sono
alla base di insidiose misconcezioni,
causate a volte dalle scelte didattiche
effettuate dagli insegnanti.
Esempio: l’altezza…maldestramente
definita alla scuola elementare e poi spesso
lasciato semplicemente all’intuizione, ma che è
causa di diffuse difficoltà tra gli studenti di
qualsiasi età.
64
Sbaragli S. (2010). Qui cade sua… altezza
Segmento o grandezza?
Di solito, nei libri di testo, si legge ad esempio
che ciascuna delle tre altezze di un triangolo è
«il segmento che “parte” da un vertice e
“cade” perpendicolarmente sul lato opposto o
sul suo prolungamento».
È lecito domarsi: l’altezza è davvero un
segmento o una grandezza? Come può un
segmento “partire” e “cadere”? Supponendo
che un segmento possa “partire”, lo deve fare
per forza da un vertice? Si parla di altezza solo
per determinate figure? Quante altezze ha un
poligono? L’altezza rappresenta quindi un
concetto all’apparenza semplice ma che
nasconde al suo interno notevoli complessità…
65
Vertice o un qualsiasi punto?
«No, questa non è l’altezza,
perché non rispetta la regola che
abbiamo imparato. L’altezza deve
partire dal vertice e scendere fino
a quando incontra la base» (V
primaria)
66
67
16
27/11/2014
Interna o anche esterna?
Verticale o qualsiasi direzione?
Questo segmento rappresenta
una delle altezze del triangolo?»
Alcuni bambini rispondono: «No,
perché non è in piedi»
«Non è un’altezza perché finisce
fuori dal triangolo» (V primaria)
68
69
70
E così, l’altezza diventa
esclusivamente verticale
dal punto di vista del
lettore...
e precisa… «In questo momento non è
un’altezza; se voglio che diventi
un’altezza, devo girare il foglio e
rimetterla in piedi»
e la dispone nel seguente modo:
Quante altezze ha un poligono?
Ad esempio il trapezio, pur essendo
costituito da 4 lati, ha per i libri di testo
un’unica altezza: la distanza tra i due lati
paralleli; mentre si potrebbe far notare
che ciascun quadrilatero, avendo 4 lati,
ha 4 altezze, una relativa a ciascun lato.
L’autista scolarizzato…
71
17
27/11/2014
«L’altezza di un trapezio è
la distanza tra due lati
paralleli».
72
Sbaragli S. (2010). Qui cade sua…
altezza.
73
74
Risulta invece interessante parlare di altezza
in modo generalizzato per qualsiasi poligono
e far sì che ogni poligono abbia un numero di
altezze pari al numero di lati.
Ciò è possibile considerando un’altezza
rispetto ad un lato come «la distanza
massima individuata dai punti del
poligono rispetto a quel lato o al suo
prolungamento o, se si preferisce,
rispetto alla retta che contiene quel
lato» (nel concetto di distanza è già implicita
la perpendicolarità).
Alla richiesta di disegnare un’altezza in un
poligono disposto nel foglio in modo che
nessuna di queste potesse essere
individuata tramite una parallela ai
margini del foglio, l’allievo disegna una
verticale dal suo punto di vista che non
era in realtà un’altezza, non essendo
perpendicolare ad un lato.
75
18
27/11/2014
Queste misconcezioni derivano dalla diversità
tra lo spazio dell’esperienza fisica che è
anisotropo, ossia possiede una direzione
privilegiata rappresentata dalla verticale, e lo
spazio isotropo della geometria euclidea,
dove tutte le direzioni per un punto si
equivalgono.
Occorre quindi curare il passaggio dallo
spazio anisotropo del bambino allo spazio
isotropo della geometria.
Sul suo libro c’era scritto che il triangolo è
isoscele quando ha i lati obliqui della
stessa lunghezza.
76
77
Sbaragli S. (2004). La
rilevazione di
misconcezioni in
geometria. Il caso
degli enti primitivi.
Che cos’è per te un punto in matematica?
A.: … non è un triangolo isoscele perché
non ha i due lati obliqui della stessa
lunghezza.
“è un punto rotondo che forma le linee” (III
media)
“per me il punto può essere una cosa
grandissima o microscopica perché è come un
cerchio di diverse misure” (IV elementare)
“il punto è una parte di piano indeterminato,
perché può avere varie dimensioni, che
costituiscono l’inizio, la fine o entrambi di un
segmento, una retta” (III media)
“non si sa ancora bene che cos’è un punto
però per me è solo un punto su un foglio che
può essere di diverse dimensioni”(IV
elementare)
“.”(Liceo)
78
“Il punto è sferico” (ins.)
“Il punto è un cerchio di diametro variabile”
(ins)
“Non credo che ci siano altri modi per
rappresentare un punto se non quello di
toccare leggermente un foglio con una penna
(ins.)
Si attribuisce a questo ente matematico:
una forma tondeggiante,
una certa dimensione variabile.
79
19
27/11/2014
Queste misconcezioni mettono in evidenza
come si confonda la rappresentazione
proposta
con l’oggetto matematico
che si vuole far apprendere.
Il punto è percepito e riferito all’unica
rappresentazione che viene comunemente
fornita dalla noosfera: un “tondino”
disegnato su un foglio, di diametro
variabile, avente una certa dimensione.
Tali
rappresentazioni
convenzionali
univoche rischiano di essere percepite
come le uniche plausibili e possibili.
80
81
“Lo studente non sa che sta apprendendo
segni che stanno per concetti e
che dovrebbe invece apprendere concetti;
se l’insegnante non ha mai riflettuto
su questo punto, crederà che lo studente
stia apprendendo concetti, mentre questi
sta in realtà ‘apprendendo’ solo a far uso
di segni”.
(D’Amore)
82
Occorre didatticamente fare molta
attenzione alla scelta, ai contesti ed
alle modalità d’uso dei segni
che rappresentano l’oggetto matematico
che si vuole far apprendere agli allievi.
83
20
27/11/2014
Le diverse rappresentazioni del punto
La varietà di rappresentazioni
permetterà agli allievi di “purificare”
l’oggetto dalle proprietà che non gli sono
proprie come: la forma, la pesantezza, il
colore, la dimensione …
per poi indirizzarli verso i saperi
“istituzionali”.
Un punto in matematica dovrebbe essere
un ente privo di dimensione,
quindi la sua rappresentazione,
necessaria per potersi capire,
potrebbe essere di qualsiasi tipo,
dato che non deve rispecchiare
nessuna caratteristica particolare,
se non quella di non poter essere eseguita.
84
85
Se chiediamo ai bambini:
Cos’è per te un punto in matematica?
Cos’è per te la linea in matematica?
Scuola dell’infanzia
Punto:
“Sono dei puntini piccoli e grossi” (Andrea 5
anni)
Linea:
“La linea matematica è un metro” (Riccardo
5 anni)
86
87
21
27/11/2014
Scuola primaria
Commento dell’insegnante
“Il punto in matematica secondo me è una cosa
importante. Ma per me può significare tre cose:
a) Il punto in un numero grande tipo
123.528.267.946 in un numero così i punti
servono per riuscire a leggere il numero;
b) C’è qualcuno che al posto del x usa il punto
esempio 14 · 5 = 70 in questa moltiplicazione il
punto serve per abbreviare;
c) Qualcun altro invece usa il punto come virgola,
esempio 194,6 o 194.6
Secondo me il modo più utile è il numero 1” (V primaria)
“Questo (suo alunno che ha scritto il TEP
riportato) ha individuato bene il punto in
matematica.
Se si chiedeva in geometria era un’altra
cosa, ma in matematica ha ragione lui: è
questo il punto”
88
90
89
“Io penso che il punto matematico sia un
punto che fa finire una frase matematica
anche per far finire i numeri” (III
elementare)
“Non si sa ancora bene che cos’è un punto
però per me è solo un punto su un foglio che
può essere di diverse dimensioni” (IV
elementare)
“Un punto in matematica è importante per
poter prendere un voto per essere felici” (I
media)
Alla domanda, ancora ambigua,
“quanti punti ci sono in un piano?”
“Dipende se i puntini sono vicini ce ne
possono essere 100, anche di più”
“Dipende da quanti ne vogliamo fare noi,
possiamo farli vicinissimi e diventano
tantissimi. Se li vogliamo fare distanti
sono pochi.”
91
22
27/11/2014
“modello della collana” che viene
indicato spesso dagli studenti come
modello adatto per rappresentarsi
mentalmente i punti sulla retta e che è
stato a volte evidenziato dagli alunni come
modello fornito dai loro insegnanti di
scuola elementare, modello che resiste ad
ogni attacco successivo (Arrigo e D’Amore,
1999; 2002)
92
94
In alcuni casi queste idee sono
state accettate, e addirittura
condivise, dagli insegnanti
intervistati.
Anche se si fanno piccoli piccoli i punti, più
di tanti non ce ne stanno in una retta.
(insegnante di scuola elementare)
93
dato che anche i bambini molto piccoli
(3-6 anni) hanno concezioni matematiche
ingenue ma profonde ottenute
empiricamente o per scambio sociale, si
potrebbe addirittura pensare che tutta la
carriera scolastica di un individuo, per
quanto attiene la matematica, sia
costituita dal passaggio da misconcezioni
a concezioni corrette.
La letteratura ha ampiamente mostrato come
molti studenti di ogni età siano convinti che
vi sia una relazione di dipendenza stretta tra i
due concetti sul piano relazionale, del tipo:
se A e B sono due figure piane, allora:
se (perimetro di A > perimetro di B) allora (area di A
> area di B)
idem con <
idem con = (per cui: due figure isoperimetriche sono
necessariamente equiestese);
e viceversa, scambiando l’ordine “perimetro – area”
con “area – perimetro”
95
23
27/11/2014
lo studente tenta di applicare la seguente
“legge di conservazione”:
Trova un
esempio per
ognuno di
questi casi:
se la tal cosa cresce, anche
quest’altra ad essa relazionata
cresce
(e viceversa)
Azhari (1998)
96
97
98
99
24
27/11/2014
Risposte Corrette: 14%
Risposte Errate: 80%
LIV 06_2013
LIV 06_2010
“Le figure
geometriche
sono regolari”
Ottagono può essere solo
un poligono regolare
Quadrato, poligono
regolare per eccellenza,
ha tutto uguale, perfino
le diagonali uguali al lato!
Risposte Corrette: 14,7%
100
101
PN_2011
“Area e
Perimetro”
“altezza”
LIV 05_2012
102
“Area e
Perimetro”
103
25
27/11/2014
livello 5 2011/12
PN_2010
“Area e
Perimetro”
104
“L’altezza è
verticale”
105
LIV 05_2012
“L’altezza è
verticale”
Cercare di costruire situazioni di
apprendimento partendo dalle prove
di valutazione standardizzate
Ambiente di apprendimento Software di
Geometria Dinamica. È noto che dinamizzare
la situazione crea un effettivo arricchimento
concettuale. (Arzarello et al, 2012, Noss,
Healy, Hoyles, 1997, Laborde et al, 2006,
Olivero & Robutti, 2007)
106
26
27/11/2014
Valutazione
standardizzata
Valutazione
formativa
Valutazione
standardizzata
Valutazione
formativa
Il software di geometria dinamica permette la costruzione e
la manipolazione di figure geometriche nel piano euclideo
e nel piano cartesiano
Perché Geogebra?
È GRATUITO
Consente una buona gestione
simbolica degli oggetti geometrici e
l’integrazione con l’ambiente
numerico
Valutazione
standardizzata
Valutazione
formativa
dinamicità, ottenuta tramite la funzione di
trascinamento (dragging);
la misura (di lunghezze di segmenti, di ampiezze
di angoli, di aree di figure, ...);
Livello
05
la traccia, il luogo, l’animazione (che
consentono di vedere l’evoluzione di modelli);
l’integrazione di registri di rappresentazione
diversi (come quello geometrico e quello
analitico), che consente di modellizzare
situazioni problematiche.
27
27/11/2014
Livello
05
Livello
06
Animazione
Animazione 2
Livello
06
Animazione
IV GEOGEBRA ITALIAN DAY - Torino, 3 ottobre 2014
28
27/11/2014
Animazione
IV GEOGEBRA ITALIAN DAY - Torino, 3 ottobre 2014
IV GEOGEBRA ITALIAN DAY - Torino, 3 ottobre 2014
Dal disegno di un triangolo
all’idea di triangolo
Spazio e figure
Relazioni
e funzioni
La situazione appena vista
è un ponte verso l’ambito
relazioni-funzioni.
Il problema
della
generalità
Ogni volta che lavoriamo su una figura geometrica, abbiamo sotto
gli occhi un modello concreto (ad es. il triangolo rettangolo)
Insegnanti
Noi insegnanti sappiamo che ci
stiamo riferendo a una famiglia
infinita di figure che
condividono con quel
particolare disegno di triangolo
alcune proprietà e non altre.
Sappiamo distinguere quali
sono le proprietà accidentali,
cioè che appartengono a quel
triangolo ma non
necessariamente a tutti gli altri.
Studenti
Elementi particolari
possono essere
considerati
fondamentali.
Entrano nelle
caratteristiche generali
alimentando così il
formarsi di
misconcezioni.
29
27/11/2014
Il problema
Dal disegno di un triangolo
della
all’idea di triangolo
generalità
Ogni volta che lavoriamo su una figura geometrica, abbiamo sotto
gli occhi un modello concreto (ad es. il triangolo rettangolo)
Ogni volta che lavoriamo su una figura geometrica,
abbiamo sotto gli occhi un modello concreto (ad es. il
triangolo rettangolo)
Caratteristiche molto forti
come impatto visivo
DISPOSIZIONE ASSUNTA (ANCHE
INCONSAPEVOLMENTE)
COME UNA CARATTERISTICA DI
OGNI TRIANGOLO RETTANGOLO
Capacità minima di
identificare un triangolo
rettangolo in questa
posizione
MOLTO FREQUENTEMENTE QUINDI GLI STUDENTI
ASSUMONO COME RAPPRESENTATIVO DI UN
CONCETTO UN ESEMPIO PROTOTIPICO IN CUI SONO
PRESENTI ANCHE CARATTERISTICHE CHE IN
REALTA’ NON APPARTENGONO ALL’IDEA GENERALE.
Con Geogebra
Tendono a riprodurre e a disegnare, ogniqualvolta un
problema o una consegna richiede di lavorare con
quella figura in generale, proprio il modello prototipico.
RAFFORZATO:
Libri di testo
Abitudini di disegno delle insegnanti
Costruire figure geometriche anche seguendo percorsi
non-standard (ad esempio come risultati di costruzioni
precedenti oppure definendo analiticamente le
coordinate dei punti)
Permette di muovere liberamente le figure
Consente di modificarle con diverse modalità
L’USO DI UN SOFTWARE DI GEOMETRIA DINAMICA
E DI UNA LIM OFFRE AGLI STUDENTI E AGLI
INSEGNANTI MOLTA PIU’ LIBERTA’ NEL REALIZZARE
E MANIPOLARE FIGURE GEOMETRICHE
30
27/11/2014
COSTRUZIONI GEOMETRICHE
Le figure vengono costruite definendo le relazioni fra gli
elementi che le compongono
C
•
•
•
•
TRACCIARE UN SEGMENTO (AB)
TRACCIARE LA RETTA PERPENDICOLARE
AD AB PER IL PUNTO B
COSTRUIRE UN SEGMENTO BC SULLA
RETTA PERPENDICOLARE
CONGIUNGERE A CON C
Trascinamento dei vertici
B
Il triangolo di Duval
La geometria coinvolge tre tipi
di processi cognitivi, che sono
tra di loro collegati
A
Sono consentiti tutti (e solo) i movimenti che
mantengono la perpendicolarità tra AB e BC (punto C
si muoverà solo lungo la direzione BC, punto B si
muoverà nel piano ma BC continuerà ad essere
perpendicolare ad AB, )
133
Visualizzazione
Visualizzazione
Il lavoro con le figure:
Su supporto materiale
Nella nostra mente
Costruzione
134
Dimostrazione
135
31
27/11/2014
Costruzione
Dimostrazione
Il lavoro con gli strumenti
Il lavoro teorico
Discorso con definizioni,
assiomi, teoremi
Riga e compasso
Software
136
137
Sono processi distinti
138
La visualizzazione non dipende dalla
costruzione, abbiamo accesso cognitivo
alle figure, indipendentemente da come le
abbiamo ottenute.
La visualizzazione è un supporto intuitivo,
talvolta necessario per trovare una
dimostrazione, ma la dimostrazione in sè
dipende solo dal corpus di proposizioni
(definizioni, assiomi, teoremi) che sono
disponibili
…
Ma nel complesso:
Ogni attività in geometria
coinvolge, almeno
implicitamente, una
comunicazione tra questi tre
tipi di processi
139
32
27/11/2014
In effetti i concetti geometrici, diversamente da
altri concetti matematici, necessitano di
rappresentazioni figurali per poter essere
compresi, ma la sola rappresentazione figurale
non è di per sé sufficiente per formare il
concetto geometrico…
“Solo con un atto mentale, un disegno può
arrivare a condividere con il concetto che
rappresenta, anche la generalità” (Mariotti
M.A.)
Fischbein (1963) Fischbein (1993)
«Una figura geometrica può essere descritta come
avente intrinsecamente proprietà concettuali. Tuttavia
una figura geometrica non è puro concetto. È
un’immagine, un’immagine visiva. Possiede una
proprietà che i concetti usuali non possiedono, cioè
include la rappresentazione mentale di proprietà
spaziali. Tutte le figure geometriche rappresentano
costruzioni mentali che possiedono simultaneamente
proprietà concettuali e figurali»
142
143
ASPETTI CONCETTUALI E FIGURALI
“l’integrazione di proprietà figurali e concettuali
in strutture mentali unitarie, con il predominio
dei vincoli concettuali su quelli figurali, non è un
processo naturale ”. (Fishbein, 1993)
Un concetto figurale è quindi una fusione, a livello
mentale, tra concetto e figura.
ASPETTI CONCETTUALI E FIGURALI
I software di geometria
dinamica sono considerati un
nuovo tipo di mediatore tra gli
aspetti figurali e concettuali
Quando uno studente risolve
un problema di geometria
opera sul concetto figurale
Che cosa vedi?
33












