ESAME DI STATO DI LICEO SCIENTIFICO

Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
PROBLEMA 1
Un trapezio isoscele è circoscritto ad una semicirconferenza di raggio 1,
in modo che la base maggiore contenga il diametro.
1. Si calcoli, in funzione dell’ampiezza x del suo angolo acuto, l’area
della superficie del trapezio, controllando che risulta:
2  cos x
S x  
sin x
2. Si studi la funzione S x  e si tracci il suo grafico  nell’intervallo
0  x  2 , mettendo in evidenza la parte di grafico compatibile con i
dati del problema.
3. Si scelga a caso un punto all’interno del trapezio e si determini la
probabilità px  che tale punto risulti interno al semicerchio inscritto.
Si studi la funzione px  e si tracci il suo grafico  nell’intervallo
0 x  2
4. Si calcoli il valore medio della funzione px  nell’intervallo
0  x   2.
RISOLUZIONE
Punto 1
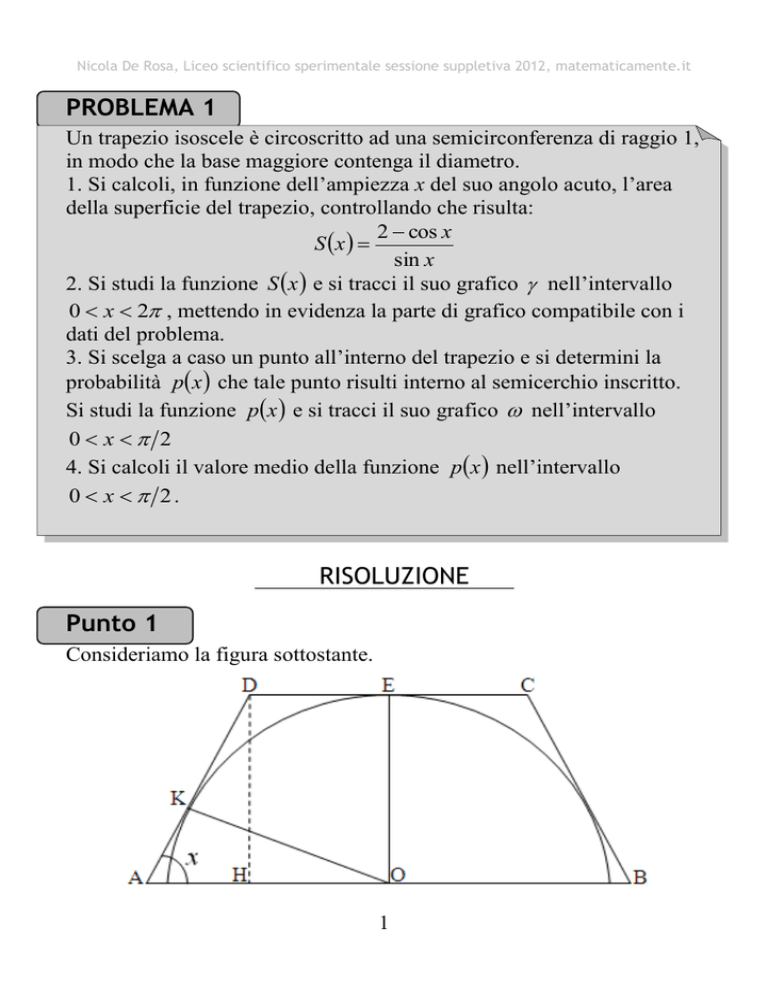
Consideriamo la figura sottostante.
1
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Sia HAˆ D  x con 0  x   2 .
Il triangolo AKO è rettangolo in K, pertanto a norma del teorema sui
KO
1
triangoli rettangoli KO  AO sin x  AO 
e la base

sin x sin x
2
maggiore del trapezio misura AB  2 AO 
; anche il triangolo
sin x
AHD è rettangolo in H pertanto applicando il toerema sui triangoli
DH
1
rettangoli DH  AH tan x  AH 
. Di conseguenza la

tan x tan x
base minore misura
1 
 1
 1  cos x 
DC  2OH  2 AO  2 AH  2

  2
 e la
 sin x tan x 
 sin x 
superficie del trapezio vale
2 
 2  2 cos x



DC  AB  DH  sin x
2  cos x
sin x 
S x  

1 
.
2
2
sin x


Punto 2
2  cos x
in 0,2 
sin x
Dominio: sin x  0  x  0  x    x  2 pertanto il dominio è
0,     ,2  ;
2  cos x
Intersezione ascisse: la funzione S x  
non si annulla mai in
sin x
quanto l’equazione 2  cos x  0 non presenta soluzioni reali dal
momento che il coseno è una funzione limitata tale per cui cos x  1 ;
Intersezioni ordinate: non ci sono intersezioni con l’asse delle ordinate
in quanto x  0 non appartiene al dominio;
Studiamo la funzione S x  
2
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Simmetrie: la funzione è dispari in quanto
2  cos x 
2  cos x
S  x  

  S x  ed è periodica di periodo
sin  x 
sin x
T  2 ;
Positività: poichè il numeratore della funzione è sempre positivo in
quanto il coseno è una funzione limitata tale per cui, la funzione sarà
positiva se il denominatore sarà positivo e quindi quando
sin x  0  0,   ;
Asintoti verticali:
lim f x   , lim f x   , lim f x   , lim  f x   
x 0
x 
x 
x2
pertanto le rette x  0, x   , x  2 sono asintoti verticali;
Asintoti orizzontali: non ha senso calcolarli in quanto il dominio è
0,     ,2  ;
Asintoti obliqui: non ha senso calcolarli in quanto il dominio è
0,     ,2  ;
1  2 cos x
Crescenza e decrescenza: la derivata prima è S ' x  
per
sin 2 x
1
cui il numeratore è positivo se cos x  e il denominatore è sempre
2
positivo nel dominio 0,     ,2  ; all’interno del dominio
0,     ,2  la disequazione cos x  1 è verificata per   x  5 .
2
3
3
Il quadro dei segni è di seguito riportato:
1  2 cos x  0
sin 2 x  0
0
-

+
3
minimo
3

5
3
massimo
+
2
x
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Dal grafico dei segni della derivata prima deduciamo che la funzione


presenta un minimo relativo in m , 3  ed un massimo relativo in
3

 5

M  , 3  .
 3

Concavità e convessità: la derivata seconda è pari a
2 cos 2 x  cos x  1
da cui deduciamo che la funzione rivolge
S ' ' x  
sin 3 x
concavità verso l’alto negli intervalli in cui sin x  0 e verso il basso
negli intervalli in cui sin x  0 , pertanto verso l’alto in 0,   e verso il
basso in  ,2  e non vi sono flessi.
Il grafico  è di seguito presentato.


Compatibilmente con i dati del problema, la parte di grafico è quella per
cui 0  x 

2
ed è di seguito presentata.
4
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Punto 3
L’area del semicerchio di raggio unitario è
  12


pertanto la
2
2
probabilità px  è data dal rapporto dell’area del semicerchio e


sin x
2
 
.
2  cos x 2 2  cos x
sin x

sin x
 
Studiamo la funzione px   
in  0,  .
2 2  cos x
 2
 
Dominio: poichè 2  cos x  0 x  R   0,  deduciamo che il
 2
 
dominio è  0,  ;
 2
Intersezione ascisse:

sin x
p x   
 0  sin x  0  x  k , k  Z quindi nessuno
2 2  cos x
dell’area del trapezio: px  
5
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
zero cade nel dominio pertanto non vi sono intersezioni con l’asse delle
ascisse;
Intersezioni ordinate: non ci sono intersezioni con l’asse delle ordinate
 
in quanto x  0 non appartiene al dominio  0,  ;
 2
Simmetrie: la funzione è dispari in quanto

sin  x 

sin x
p x   
 
  px  ed è periodica di
2 2  cos x 
2 2  cos x
periodo T  2 ;
Positività: poichè il denominatore della funzione è sempre positivo in
quanto il coseno è una funzione limitata tale per cui cos x  1 , la
funzione sarà positiva se il numeratore sarà positivo e quindi quando
 
sin x  0 ; poiché nell’intervallo  0,  il seno è non negativo,
 2
deduciamo che la funzione è non negativa in tutto il dominio;
Asintoti verticali: lim px   0, lim px  
x 0
x


4
pertanto non vi sono
2
asintoti verticali;
Asintoti orizzontali: non ha senso calcolarli in quanto il dominio è
 
 0,  ;
 2
 
Asintoti obliqui: non ha senso calcolarli in quanto il dominio è  0,  ;
 2
 2 cos x  1
Crescenza e decrescenza: la derivata prima è p' x   
2 2  cos x 2
1
per cui il numeratore è positivo se cos x  e il denominatore è sempre
2
 
 
positivo nel dominio  0,  ; all’interno del dominio  0,  la
 2
 2
6
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
1
 
è verificata per x   0,  . Il quadro dei
2
 3
segni è di seguito riportato:
disequazione cos x 
2 cos x  1  0
2  cos x 2
0
+


3
2
massimo
Dal grafico dei segni della derivata prima deduciamo che la funzione
  3 
.
presenta un massimo relativo in M  ,

3 6 
Concavità e convessità: la derivata seconda è pari a
cos 2 x
; poiché sia il seno che il coseno sono positivi in
p' ' x    
sin 3 x
 
 0,  deduciamo che la funzione volge concavità verso il basso in
 2
 
 0,  e non vi sono flessi.
 2
Il grafico  è di seguito presentato.
7
x
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Punto 4
Il valore medio è pari a

VM 

2
1

2
 p  x  dx 
0 0

2
2 
sin x 
 sin x 

dx




 dx 


 0  2 2  cos x 
2

cos
x


0
2

 ln  2  cos x   02  ln 2
8
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
PROBLEMA 2
Si consideri la funzione:
f x   arctan x 
x
1 x2
1. Si studi tale funzione e si tracci il suo grafico  , su un piano riferito
ad un sistema di assi cartesiani ortogonali Oxy.
2. Si verifichi che i tre punti di flesso di  sono allineati e si scriva
l’equazione della retta alla quale essi appartengono.
3. Si scrivano le equazioni delle tangenti inflessionali, si dimostri che
due di esse sono parallele e si calcoli la loro distanza.
4. Si calcoli l’area della superficie piana, delimitata dalla curva  ,
dall’asse x e dalle rette di equazione x  1 e x  3 .
RISOLUZIONE
Punto 1
Studiamo la funzione f x   arctan x 
x
1 x2
Dominio: R;
Intersezione ascisse: f x   arctan x 
x
x
e tale
 arctan x 
2
1 x
1 x2
equazione la si può studiare o per via grafica trovando i punti di
x
intersezione della funzione y  arctan x con la funzione y 
1 x2
x
oppure si può notare che la funzione f x   arctan x 
è
1 x2
strettamente crescente nel dominio in quanto ha derivata prima
2x 2


f ' x  
e inoltre lim f x    e lim f x  
pertanto a
2
2
x 
x


2
2
x 1


norma del teorema degli zeri   , : f    0 f x   0 e data la
9
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
stretta crescenza questa radice è unica. Poichè da un controllo diretto si
nota subito che f 0  0 , deduciamo che l’unica intersezione con l’asse
delle ascisse è x  0 ;
Intersezioni ordinate: x  0  f 0  0 ;
Simmetrie: è una funzione dispari in quanto
 x    arctan x  x   f x ;
f  x   arctan  x  
2
1 x2
1   x 
x
x
Positività: f x   arctan x 
; se
 0  arctan x 
2
1 x
1 x2
x
grafichiamo entrambe le funzioni y  arctan x e y 
in un
1 x2
unico sistema di riferimento cartesiamo, possiamo notare che
f x   0  x  0 come di seguito mostrato.
Asintoti verticali: non ve ne sono in quanto il dominio è R;
Asintoti orizzontali: lim f x   
x 
y

2

2
e lim f x  
x  

2
per cui le rette
sono asintoti orizzontali;
Asintoti obliqui: non ve ne sono in quanto lim
x  
10
f x 
0 ;
x
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Crescenza e decrescenza: la derivata prima come già detto
2x 2
precedentemente è f ' x  
per cui la funzione è strettamente
2
x2 1
crescente in tutto R;
4x 1  x 2
Concavità e convessità: la derivata seconda è f ' ' x  
e
3
x2 1
risulta essere positiva in  ,1  0,1 e negativa in  1,0  1, ,
pertanto la funzione volge concavità verso l’alto in  ,1  0,1 e
verso il basso in  1,0  1, e presenta tre flessi di cui
1     1

F1   1,  , F2 1,   a tangente obliqua e F3 0,0 a tangente
2 4   4 2

orizzontale; infatti in x  0 si annulla anche la derivata prima e non si
annulla la derivata terza il cui calcolo si lascia al lettore.
Il grafico  è di seguito presentato:






Punto 2
I tre punti di flesso sono allineati lungo la retta di equazione
 1 
y    x .
 4 2
11
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Punto 3
La tangente inflessionale in F3 0,0 ha equazione y  0 .
La
tangente
inflessionale
in
1 
dove

2 4
1
1  x

y  x  1     1  .
2
2 4 2
4
y  mx  1 
La
tangente
y  mx  1 
inflessionale

in
1
dove
4 2
1
 1 x 
y  x  1      1 .
2
4 2 2 4

1 

F1   1,  
2 4

1
m  f '  1 
2
  1
F2 1,  
 4 2
1
m  f ' 1 
2
ha
equazione
e
ha
cioè
equazione
e
cioè
1 

  1
Quindi le tangenti inflessionali in F1   1,   e F2 1,   ,
2 4

 4 2
avendo lo stesso coefficiente angolare, sono parallele e per calcolarne la
1 

distanza basta calcolare ad esempio la distanza di F1   1,   da
2 4

x 
x 
y    1 ; l’equazione della retta y    1 in forma implicita
2 4
2 4
1 

è 2 x  4 y    4  0 pertanto la distanza di F1   1,   da essa è
2 4

1  
2   1  4        4
 2  2    4 4 
2 4
d


.
2 5
5
22  42
12
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Punto 4
L’area richiesta è di seguito raffigurata in grigio.
Essa vale
x 

S    arctan x 
dx ; applicando l’integrazione per parti si ha:
1 x2 
1
3
3
3
x 

 x 
 x 
3
S    arctan x 
dx  x arctan x 1   
dx   
dx 
2 
2 
2 
1 x 
1
1 1  x 
1 1  x 
3


3
 2x 
3
 x arctan x 1   
dx  x arctan x  ln 1  x 2
2 
1 1  x 


 
  4 3  3 
  3   ln 4     ln 2   
  ln 2
3

 4
  12 
13

1
3

Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
QUESTIONARIO
Quesito 1
Si divida il segmento in due parti AC e CB, in modo che, costruito su
AC il quadrato ACDE e su CB il triangolo equilatero CBF, sia minima
l’area del pentagono ABFDE.
Consideriamo la figura sottostante.
K
E
A
F
D
C
H
B
Poniamo BC  x, AC  a  x con 0  x  a . L’area del pentagono
ABFDE è la somma dell’area del quadrato ACDE, del triangolo
equilatero CBF e del triangolo scaleno DCF. L’area del quadrato ACDE
2
è S  ACDE   a  x  , l’area del triangolo equilatero CBF è
S CBF  
3 2
x mentre il triangolo scaleno DCF ha la base DC che
4
CB a  x 

misura a  x e l’altezza KF che misura
e pertanto ha area
2
2
xa  x 
S DCF  
. Quindi
4
3 2 xa  x   3  3  2 7a
2
x 
S ABFDE x   a  x  
x 
 
x  a 2 con

4
4
4
 4 
14
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
0  x  a ; tale area non è altro che una parabola con concavità rivolta
verso l’alto, pertanto il minimo è raggiunto nell’ascissa del vertice
 7a 
 
7 3 3
4 
x min   

a e l’area minima vale
12
 3  3

2

4


 51  47 3  2
a .
S x min   

288




Quesito 2
Data la funzione:
sin x  log sin 2 x , per 0  x   2,
f x   
per x  0,
0
si provi che è continua, ma non derivabile, nel punto x = 0.
Calcoliamo il limite destro lim sin x  logsin 2 x  ; esso può essere
x 0
log sin 2 x 

e si presenta nella forma indeterminata
1

sin x
pertanto applicando il teorema di De l’Hopital si ha
2 cos 2 x
log sin 2 x 
 cos 2 x  sin x 
lim
 lim 2 sin 2 x  lim  
  0 di
x 0 
x 0
1
cos x x0 
cos 2 x 

sin x
sin 2 x
conseguenza la funzione è continua in x  0 .
Per la derivabilità calcoliamo la derivata prima della funzione
f x   sin x  logsin 2 x  :
cos 2 x
cos 2 x
f ' x   cos x  log sin 2 x   sin x  2 
 cos x  log sin 2 x  
sin 2 x
cos x
scritto come lim
x 0
15
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
e valutiamola per x  0  :
cos 2 x 

lim cos x  log sin 2 x  
 1  log 0  1  
x 0 
cos x 
pertanto lim f ' x    e di conseguenza la funzione non è derivabile
x 0
in x  0 .
Quesito 3
Si scriva l’equazione della tangente al diagramma della funzione
loge  2 x 
f  x    x  2
nel punto P0,2 ?
Il logaritmo presente nella funzione è da intendersi in base e, pertanto in
seguito lo indicheremo con ln. La tangente ha equazione y  mx  2
con m  f ' 0 . Per calcolarne la derivata scriviamo la funzione
f  x    x  2
derivata prima è
ln e  2 x 
come f x   e ln  x2 
ln  e  2 x 
  e ln x2 lne2 x  la cui
2 
 1
f ' x   e ln  x  2 ln e  2 x   
 ln e  2 x   ln x  2 

e  2 x 
x  2
2 
ln e  2 x   1
 x  2

 ln e  2 x   ln x  2 
e  2 x 
x  2
4 ln 2
 ln e 2 ln 2 
 1 2 ln 2 
pertanto m  f ' 0  2 ln e  
e

  2 
  1
e 
e 
e
 2
2
 4 ln 2 
di conseguenza la tangente ha equazione y  1 
x  2 .
e 

16
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Quesito 4
La superficie piana S, delimitata dalla curva  di equazione
y  1 tan x e dall'asse x nell'intervallo 0  x   4 , è la base di un
solido  , le cui sezioni, ottenute con piani perpendicolari all'asse x,
sono tutte triangoli equilateri. Si calcoli il volume di  .
Ogni sezione è un triangolo equilatero di area S x  
3
1  tan x 2
4
pertanto il volume del solido  so ottiene integrando la superficie
3
1  tan x 2 in 0,   :
S x  
4
 4


4
4
V     S x dx 
0



3
34
2


1

tan
x
dx

1  tan 2 x  2 tan x dx 


4 0
4 0




3 
sin 2 x
3 4  1  cos 2 x



dx 

1


2
tan
x
dx

1


2
tan
x
2



4 0  cos 2 x
4
cos
x


0
4



3 4 1
sin x 
3
4 



2
dx

tan
x

2
ln
cos
x


0
4 0  cos 2 x
cos x 
4

3 
2 
3
 
1  ln 2
1  2 ln

4 
2 
4
17
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Quesito 5
Mentre corre con una velocità costante attraverso il deserto, montando il
suo fido cammello, un capo tuareg vede la cima di una grande palma e
dirige direttamente verso di essa. Al primo avvistamento la cima della
palma si presentava con un angolo di elevazione di 4°; venti minuti più
tardi l’angolo di elevazione misura 9°. Quanti minuti sono ancora
necessari al tuareg per raggiungere l’albero?
Consideriamo la figura seguente.
Con riferimento alla figura soprastante, sia x la distanza percorsa in 20
minuti, y la distanza da percorrere e h l’altezza della palma. Dall’ipotesi
di velocita costante si deduce che se la distanza x è stata percorsa in 20
y
minuti la distanza y sarà percorsa in t  20 minuti. D’altra parte il
x
triangolo ACD è rettangolo pertanto h  y tan9  x  y  tan4 da
x  y   tan9  x  tan9  tan4  y 
tan4
cui
y
tan4
y
tan4
x tan9  tan4
e in conclusione il tempo da percorrere ancora è
y
20  tan4
t  20 
 15,8 minuti.
x tan9  tan4
18
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Quesito 6
ax 2  4
perché la curva
bx  2
rappresentativa ammetta asintoto di equazione y  x  2 .
Si determinino i coefficienti dell’equazione y 
L’asintoto
obliquo
ha
equazione
 ax 2  4 


bx  2 
 ax 2  4  a


m  lim
 lim  2
x  
x   bx  2 x 
x

 b
y  mx  q
con
e
 ax 2  4 a 
 abx 2  4b  abx 2  2ax 
 4b  2ax 
  lim  2
q  lim 
 x   lim 

2
x  bx  2
b  x
b x  2b

 x b x  2b 
.
a
 b  1
Imponendo
il
sistema
si
ottiene

2
a

2
 b 2
a  b
a  b
a  1


pertanto la curva con asintoto
 2

 2a
 b 2  2  a  2 b  1
 x2  4
obliquo y  x  2 ha equazione y 
e corrisponde alla retta di
x2
equazione y  x  2 ( l’asintoto stesso) privata del suo punto di ascissa
2.
19
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Quesito 7
Tenuto conto che:

2
cos x
dx
1  sin x
0
si calcoli un’approssimazione di log 2 , utilizzando uno dei metodi di
integrazione numerica studiati.
log 2  

2
Innanzitutto
proviamo
cos x
dx .
1

sin
x
0
log 2  
che
Si
ha


cos x
2  ln 2 .


dx

ln
1

sin
x
0 1  sin x
0
Come metodo di integrazione numerica, utilizziamo il metodo dei
 
trapezi. Si suddivide l’intervallo 0,  in 4 intervalli di ampiezza
 2



3

, x4  cui
h  mediante i 5 punti x0  0, x1  , x2  , x3 
8
4
8
2
8
corrispondono i valori della funzione
y0  f  0   1
2
 
1  
cos  
cos   
8
 
  
2 4 
y1  f   
 8  1  sin    1  sin  1   
 


8
2 4
20
 
1  cos  
4
2 2
2

 
1  cos   2  2  2
4
1
2
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
 
2
cos  
2
4
 

y2  f   
 2 
 2  1,

2 2 2
 4  1  sin  
1

 
4
2
 3 
 1 3 
cos  
cos   
3

8
 
  
2 4  
y3  f   
 8  1  sin  3  1  sin  1  3 
 


 8 
2 4 
 3 
1  cos  
 4 
2 2 .
2

,
 3  2  2  2
1  cos  
 4 
1
2
 
y4  f    0
2
L’area approssimata è


0 y  y
cos x


2
0 1  sin xdx  4  0 2 4  y1  y2  y3  
2
 1
2 2
2 2
 
 2 1
8  2 2 2 2
2 2 2

con un errore


  0, 6995




  0
3
2
  max f ' ' x     max f ' ' x 
 max f ' ' x   
a,b
1536  0 , 
12  4 2  0 , 
3
εn 
b  a 3
12n 2

in cui la derivata seconda è f ' ' x  
2

2
2 cos x
; il massimo di f ' ' x 
1  sin x 2
 
in 0,  è assunto per x  0 e vale max f ' ' x   2 pertanto l’errore
 
 2
0, 

commesso è ε n 

3
2 

3
2
 0,04 . Infatti il valore reale di log 2 è
1536
768
0,6931 e la differenza tra il valore approssimato e quello reale è
0,6995  0,6931  0,0064  0,04 .
21
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
Quesito 8
Sia C la curva d’equazione y  x 2  2 x  4 , e sia G la curva simmetrica
di C rispetto all’asse y. Qual è l’equazione di G?
L’equazione della curva G simmetrica di C rispetto all’asse delle
ordinate è yG  x   yC   x   x 2  2 x  4
Quesito 9
Si determini la probabilità che nel lancio di due dadi si presenti come
somma un numero dispari. Lanciando 5 volte i due dadi, qual è la
probabilità di ottenere come somma un numero dispari almeno due volte?
Lanciando una coppia di dadi non truccati, le possibili combinazioni di
risultati sono 6 2  36 con distribuzione equa di risultati con somma
pari o dispari, pertanto la probabilità che nel lancio di due dadi si
1
presenti come somma un numero dispari è p  . La probabilità di
2
ottenere un risultato X dispari k volte in n lanci è dato dalla
22
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
n
nk
distribuzione binomiale P X  k     p k 1  p  , pertanto la
k 
probabilità richiesta è
0
5
1
4
 5  1   1   5  1   1 
P X  2  1  P X  0  P X  1  1                   
 0  2   2  1  2   2 
5
5
5
5
5
5!  1 
3 13
1
1
1
1
 1   
       5     1  6     1 

4!1!  2 
16 16
2
2
2
2
Quesito 10
Si scelga a caso un punto all’interno di un parallelogramma, avente i
lati lunghi rispettivamente 8m e 6m e gli angoli acuti di 30°. Si
determini la probabilità che la sua distanza da ogni vertice sia maggiore
di 2m.
Consideriamo la figura seguente.
Con riferimento alla figura, possiamo ricavare la probabilità richiesta
come rapporto tra l’area della figura ottenuta sottraendo al
parallelogramma i settori circolari AGF, HBK, JCL, DNM e l’area del
parallelogramma stesso, avendo appurato che tali settori non si
sovrappongono (nel caso dei settori centrati in A e C la cosa è
abbastanza evidente, mentre nel caso dei vertici B e D bisogna
verificare che la loro distanza sia maggiore di 4, cosa che, se pur di
poco, è vera..). I settori nei vertici di 30° hanno un’area ciascuno pari a
1/12 del cerchio di raggio 2, cioè complessivamente un’area pari a
23
Nicola De Rosa, Liceo scientifico sperimentale sessione suppletiva 2012, matematicamente.it
1 
 2
2     22  
m 2 , quelli nei vertici di 150° hanno un’area
2 6
 3
ciascuno pari a 5/12 del cerchio di raggio 2, cioè complessivamente
 1 5 2  10
un’area pari a 2   
2  
m 2 . L’area del parallelogramma è
3
2 6

2
pari a 6  8  sin30  24 m , pertanto la probabilità richiesta è
2 10
24 

3
3  24  4  1    47,64% .
p
24
24
6
24