I
z
h
R2
I
R1
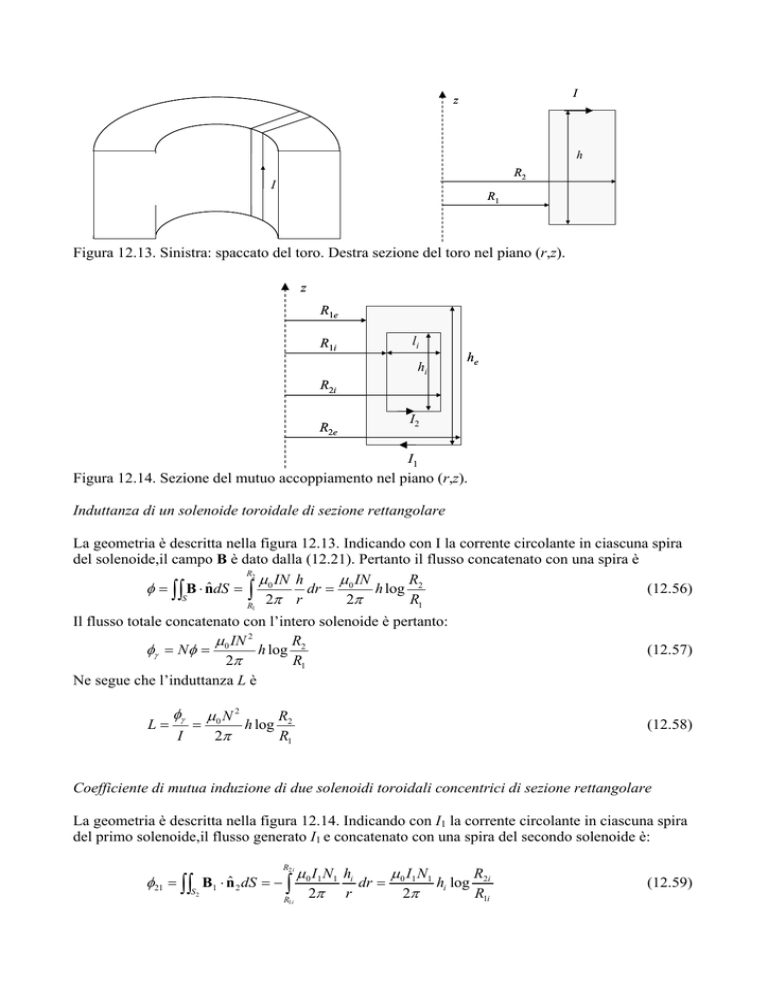
Figura 12.13. Sinistra: spaccato del toro. Destra sezione del toro nel piano (r,z).
z
R1e
R1i
li
hi
he
R2i
R2e
I2
I1
Figura 12.14. Sezione del mutuo accoppiamento nel piano (r,z).
Induttanza di un solenoide toroidale di sezione rettangolare
La geometria è descritta nella figura 12.13. Indicando con I la corrente circolante in ciascuna spira
del solenoide,il campo B è dato dalla (12.21). Pertanto il flusso concatenato con una spira è
R2
µ IN h
µ IN
R
φ = ∫∫ B ⋅ nˆ dS = ∫ 0
dr = 0 h log 2
(12.56)
S
2π r
2π
R1
R1
Il flusso totale concatenato con l’intero solenoide è pertanto:
µ IN 2
R
φγ = Nφ = 0
h log 2
2π
R1
Ne segue che l’induttanza L è
L=
φγ
I
=
µ0 N 2
R
h log 2
2π
R1
(12.57)
(12.58)
Coefficiente di mutua induzione di due solenoidi toroidali concentrici di sezione rettangolare
La geometria è descritta nella figura 12.14. Indicando con I1 la corrente circolante in ciascuna spira
del primo solenoide,il flusso generato I1 e concatenato con una spira del secondo solenoide è:
R2 i
φ21 = ∫∫ B1 ⋅ nˆ 2 dS = − ∫
S2
R1i
µ 0 I1 N1 hi
µIN
R
dr = 0 1 1 hi log 2i
2π r
2π
R1i
(12.59)
Il segno meno dipende dal fatto che, per I1>0, con riferimento al verso assunto in fig. 12.14 per I1, il
campo B1 prodotto da I1 risulta opposto alla normale n̂ 2 alla superficie S2 del secondo solenoide,
orientata in modo congruente al verso assunto per I2.
Il flusso totale concatenato col secondo solenoide è pertanto:
R
µINN
φγ 2 = N 2φ21 = − 0 1 1 2 hi log 2i
(12.60)
2π
R1i
Ne segue che il coefficiente di mutua induzione M è
M =
φγ 2
=−
µ 0 N1 N 2
R
hi log 2i
2π
R1i
I1
Infine, confrontando M2 con L1L2, si ha:
R
µ2N 2N 2
M = 0 1 2 2 hi2 log 2i
R1i
4π
(12.61)
2
2
L1 L2 =
R µ N2
R
µ 0 N12
he log 2 e 0 22 hi log 2i =
2π
R1e 4π
R1i
(12.62)
R
R
µ 02 N12 N 22
he hi log 2 e log 2i > M 2
2
R1e
R1i
4π
Se ne conclude che in questo caso l’accoppiamento tra i due solenoidi non perfetto.
Il coefficiente di accoppiamento k è:
R
log 2i
M
R1i
h
= i
k=
L1 L2 he log R2 e
R1e
13.
(12.63)
Misura della caratteristica B-H
La caratteristica B-H può essere misurata con l’apparato sperimentale mostrato in fig. 13.1. Il
materiale magnetico è collocato all’interno di un solenoide toroidale come quello discusso nel
paragrafo 12. L’avvolgimento è costituito da N1 spire percorse da una corrente i la cui intensità può
essere variata opportunamente, ad esempio con una resistenza1 variabile collegata ad un generatore
sinusoidale. Un’altra resistenza in serie può consentite di associare il valore vH(t) della differenza di
potenziale ai suoi morsetti alla corrente i:
vH(t)=RHi(t)
(13.1)
Le linee di campo, come già si è visto, sono circonferenze con il centro sull’asse di simmetria del
toro e che si sviluppano all’interno del toro stesso concatenando le N1 spire dell’avvolgimento. Il
campo magnetico è pertanto determinato dalla sola legge della circuitazione, che, applicata alla
generica circonferenza γ di raggio r, fornisce
∫γ H ⋅ dl = H ∫γ dl = H 2πr = N i
1
1
La regolazione dell’intensità della corrente può essere ottenuta più convenientemente con un Variac, un autotrasformatore a rapporto spire variabile.
(13.1)
Supponendo che il raggio maggiore R dell’avvolgimento toroidale sia grande rispetto alla
dimensione della sua sezione, possiamo ignorare la variazione di r all’interno della sezione ed
approssimare r con un raggio medio di valore R. Risulta quindi
Ni Ni
H= 1 ≅ 1
(13.2)
2πr 2πR
Per misurare B si può far riferimento alla legge dell’induzione (12.27). A questo scopo avvolgiamo
sul toro un altro circuito costituito da N2 spire e chiuso con una impedenza elevata, in modo da
assorbire una corrente trascurabile. In tal modo il campo H non subisce apprezzabili variazioni.
Con riferimento alla fig.13.2, la tensione indotta sulle N2 spire, nell’ipotesi che queste siano
realizzate con un conduttore di resistività trascurabile, risulta essere:
−
dφγ
dt
=
E ⋅ tˆdl = ∫ E ⋅ tˆdl + ∫ E ⋅ tˆdl = V
∫
γ
γ
γ
B iA
spira
AB
(13.3)
A eB
Considerando il campo d’induzione B parallelo ad H e praticamente costante all’interno del toro, si
ha per il flusso φγ
φγ = ∫∫ B ⋅ nˆ dS = N 2 ∫∫ B ⋅ nˆ dS + ∫∫ B ⋅ nˆ dS ≅ N 2 B ∫∫ dS = N 2 BS
Sγ
e quindi
B=
S
Sext
S
φγ
N2S
Nella (13.4) si è tenuto conto che l’induzione magnetica al di fuori del circuito magnetico è
trascurabile e, pertanto, φγ non dipende dalla forma di γext.
L’induzione magnetica B può essere quindi ottenuta integrando nel tempo la tensione Vab:
(13.4)
(13.5)
t
φγ (t ) = φγ (0) + ∫ V AB (t )dt
(13.6)
0
L’integrazione può essere facilmente ottenuta con un circuito integratore, quale è ad esempio un
circuito RC (fig 13.3) con una costante di tempo RC molto elevata rispetto al periodo della forma
d’onda del generatore sinusoidale che alimenta l’avvolgimento di N1 spire. Con riferimento al
circuito di fig. 13.3, si ha infatti:
dv
RC B + v B = V AB (t )
(13.7)
dt
RC
dv B
≅ V AB (t )
dt
(13.9)
E quindi
t
v B (t ) = v B (0) +
1
V AB (t )dt
RC ∫0
Riassumendo, si ha che le due tensioni sono proporzionali rispettivamente ad H ed a B:
2πR
H
v H = R H i = R H
N 1
(13.10)
t
1
1
1
V AB (t )dt =
φγ =
N 2 S B
∫
RC 0
RC
RC
Esse possono quindi consentire di tracciare la caratteristica B-H, utilizzando, ad esempio, un
oscilloscopio, in cui i morsetti associati alla deflessione orizzontale sono alimentati da vH e quelli
della deflessione verticale sono alimentati da vB. Il diagramma che si ottiene, nel caso di un
materiale ferromagnetico è riportato schematicamente in fig. 13.3.
vB =
vH(t)
R
VAB(t)
vB(t)
C
Figura 13.1 Un apparato sperimentale che consente di misurare la caratteristica B-H
γint
A
B
γext
S
…
Sext
S
γint
γ’ext
A
γext
∆S
B
Figura 13.2 I riferimenti per il calcolo della tensione VAB sulla curva gamma2
Figura 13.3 La curva del ciclo d’isteresi ottenuta in risposta ad una corrente sinusoidale












