1 - Digilander

Geometria Analitica Domande e Risposte
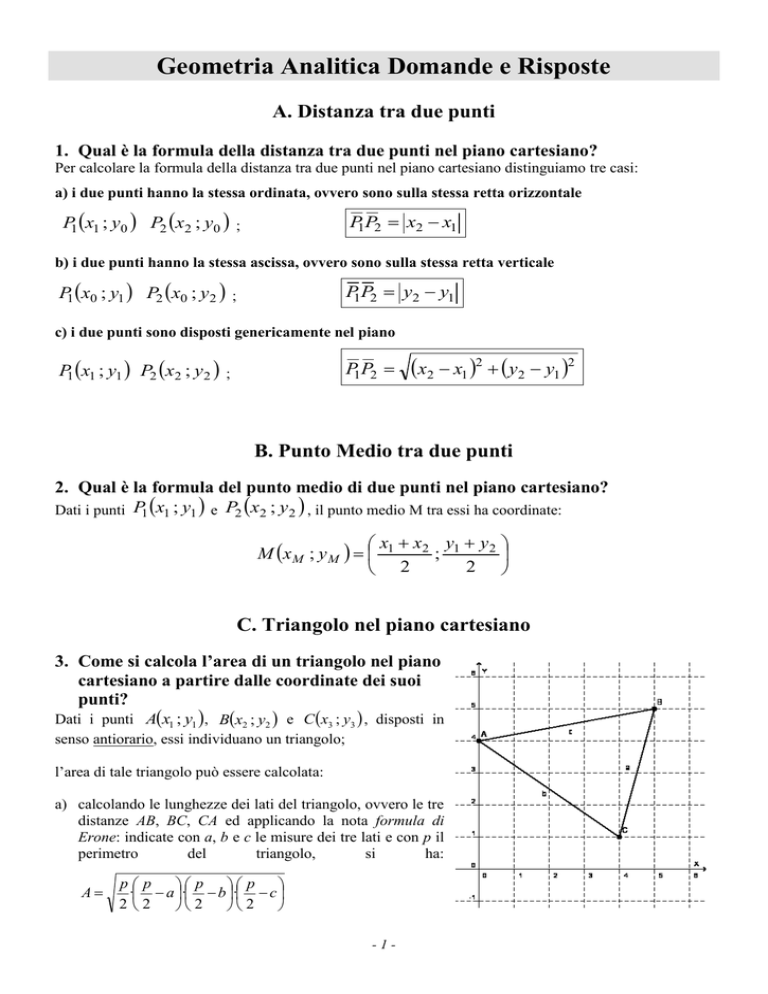
A. Distanza tra due punti
1. Qual è la formula della distanza tra due punti nel piano cartesiano?
Per calcolare la formula della distanza tra due punti nel piano cartesiano distinguiamo tre casi:
a) i due punti hanno la stessa ordinata, ovvero sono sulla stessa retta orizzontale
P1 x1 ; y0  P2 x2 ; y0  ;
P1P2  x2  x1
b) i due punti hanno la stessa ascissa, ovvero sono sulla stessa retta verticale
P1 x0 ; y1  P2 x0 ; y2  ;
P1P2  y2  y1
c) i due punti sono disposti genericamente nel piano
P1 x1 ; y1  P2 x2 ; y2  ;
P1P2 
x2  x1 2   y2  y1 2
B. Punto Medio tra due punti
2. Qual è la formula del punto medio di due punti nel piano cartesiano?
Dati i punti P1 x1 ; y1  e P2 x2 ; y 2  , il punto medio M tra essi ha coordinate:
 x  x2 y1  y 2 
M x M ; y M    1
;

2 
 2
C. Triangolo nel piano cartesiano
3. Come si calcola l’area di un triangolo nel piano
cartesiano a partire dalle coordinate dei suoi
punti?
Dati i punti Ax1 ; y1 , Bx2 ; y2  e C x3 ; y3  , disposti in
senso antiorario, essi individuano un triangolo;
l’area di tale triangolo può essere calcolata:
a) calcolando le lunghezze dei lati del triangolo, ovvero le tre
distanze AB, BC, CA ed applicando la nota formula di
Erone: indicate con a, b e c le misure dei tre lati e con p il
perimetro
del
triangolo,
si
ha:
A
pp
 p
 p 
·  a ·  b ·  c 
22
 2
 2

-1-
b) molto più semplicemente mediante la seguente formula che fa uso di un determinante del 3° ordine:
x1
1
A  x2
2
x3
y1 1
y2 1 .
y3 1
x1
Il determinante x2
x3
x1
x2
x3
y1 1 x1
y2 1  x2
y3 1 x3
y1 1
y 2 1 può essere calcolato con la nota regola di Sarrus:
y3 1
y1 1 x1
y2 1 x2
y3 1 x3
y1
y2  x1 ·y2  x3 ·y1  x2 ·y3  x3 ·y2  x1 ·y3  x3 ·y2 
y3
-2-