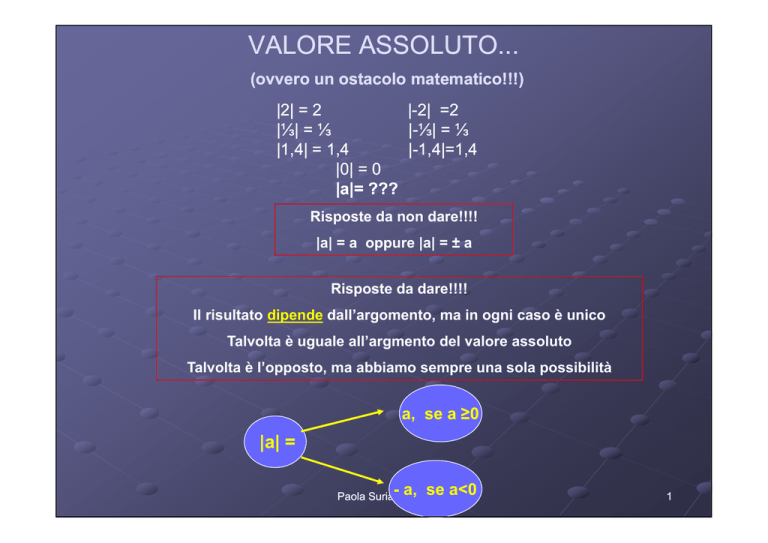
VALORE ASSOLUTO...
((ovvero un ostacolo matematico!!!))
|2| = 2
|-2| =2
|⅓| = ⅓
|-⅓| = ⅓
|1 4| = 1,4
|1,4|
14
|-1,4|=1,4
|1 4|=1 4
|0| = 0
|a|= ???
Risposte da non dare!!!!
|a| = a oppure |a| = ± a
Risposte da dare!!!!
Il risultato dipende dall’argomento, ma in ogni caso è unico
Talvolta è uguale all’argmento del valore assoluto
Talvolta è l’opposto, ma abbiamo sempre una sola possibilità
a, se a ≥0
|a| =
a, se
Paola Suria-Arnaldi
a<0
1
Valore assoluto per le soluzioni di equazioni
e disequazioni
|x| = 2
|x| = 1
x = |1|
|x| = -1
x2 = 1
x2 = 4
x2 = 9
x2 = 5
x 2 = -1
è equivalente a
x= 2
è equivalente a
x= 1
forse hai sbagliato a mettere il modulo; x =1
è impossibile, perché nessun numero reale ha valore assoluto
negativo
Æ
x = 1 Æ |x| = 1 (scrittura più elegante!)
Æ
x = 2 Æ |x| = 2
Æ
|x| = 3
Æ
|x| = √5
Æ
impossibile
x2 > 1
x2 > 4
x2 < 4
x2 < 1
x2 > - 1
x 2 < -1
x2 > 0
x2 < 0
x2 ≥ 0
x2 ≤ 0
Æ
no !!!! x > 1 (non ha senso la scrittura) Æ |x| > 1 oppure x<x<-1 V x>1
Æ |x|>2 oppure x<
x<--2 V x > 2
Æ |x| < 2 oppure -2 < x < 2
Æ |x| < 1 oppure -1 < x < 1
Æ qualsiasi x reale
Æ nessun valore di x!
Æ (un quadrato maggiore di zero?) Æ x ≠ 0
Æ nessun valore di x
Æ qualunque x reale di x
Æ solo x =0 soddisfa la disequazione
Paola Suria Arnaldi
2
Approfondiamo graficamente il legame tra
valore assoluto – equazioni/disequazioni di II °
x2 = 1
x2 > 1
x2 < 1
-5
-1
1
1
-3
-2
2
-1
1
3
5
1
I due intervalli, colorati in rosso, si possono leggere:
•
x < -1 V x > 1
•
|x| > 1
cioè
i numeri che hanno modulo maggiore di 1!! (-5, -3, -2.... , 2, 3, 5...)
x2 = 1
Æ
x2 > 1
Æ
x2 < 1
Æ
x=±1
x < -1 V x > 1
-1 < x < 1
oppure
|x| = 1
oppure
|x| > 1
oppure
|x| < 1
Paola Suria Arnaldi
3
Radici di indice pari
1 In campo reale la radice,
1.
radice di indice pari,
pari di un numero reale è possibile se e
solo se l’argomento a non è negativo Æ a ≥ 0
2. Il risultato di una radice di indice pari è sempre non negativo, se la radice è
preceduta dal segno +
+, negativo se preceduta dal segno Paola Suria Arnaldi
4