Crisi della fisica classica - Liceo Classico Scientifico XXV Aprile

Complementi alle lezioni di “Fondamenti di Struttura della Materia”
Laurea Magistrale in Fisica - a.a. 2014/2015 - Università degli Studi di Cagliari
Crisi della fisica classica
Luciano Colombo
Dipartimento di Fisica - Università degli Studi di Cagliari
Cittadella Universitaria, 09042 Monserrato (Ca)
La riproduzione, anche parziale, di questa Dispensa in qualsivoglia formato cartaceo, elettronico o virtuale
è severamente vietata.
Si invita il Lettore ad inviare segnalazione di eventuali errori o ambiguità al seguente indirizzo di posta
elettronica: [email protected]
Presentazione
Questa Dispensa è messa a disposizione degli Studenti sul sito
http://people.unica.it/lucianocolombo/didattica/materiale-didattico/
ed è intesa come semplice complemento alle lezioni tenute dal prof. Luciano Colombo durante il secondo
semestre dell’a.a. 2014/2015, nell’ambito del corso “Fondamenti di Struttura della Materia” - Laurea
Magistrale in Fisica, dell’Università degli Studi di Cagliari.
E’ doveroso sottolineare che questi appunti non rappresentano un trattato completo; sono, piuttosto, da intendere come un semplice ausilio didattico offerto allo Studente, principalmente finalizzato a
completare le lezioni frontali.
Lo stile di scrittura è, dunque, molto conciso e le dimostrazioni sono spesso solo schematicamente
illustrate, lasciando alla cura dello Studente la ricostruzione dettagliata di tutti i passaggi.
2
Indice
1 Inquadramento storico
4
2 Il calore specifico dei gas e dei solidi
2.1 Teoria cinetica dei gas . . . . . . . . . . . . .
2.2 Energia interna di un gas monoatomico ideale
2.3 Calori specifici di gas mono– e bi–atomici . .
2.4 Calori specifici dei solidi . . . . . . . . . . . .
.
.
.
.
5
5
7
8
10
3 Lo spettro del corpo nero
3.1 Gli esperimenti e la teoria classica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 La teoria quantistica di Planck . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
14
16
4 L’effetto fotoelettrico
18
. . . . . . . . . .
ed equipartizione
. . . . . . . . . .
. . . . . . . . . .
5 La fisica dei quanti
5.1 Spettri atomici . . . . . . . . . . . . . . . . . . . . . . .
5.2 Il modello di Bohr per l’atomo di idrogeno . . . . . . . .
5.3 Estensioni del modello di Bohr . . . . . . . . . . . . . .
5.4 L’ipotesi di de Broglie ed il dualismo onda–corpuscolo .
5.5 Il principio di indeterminazione di Heisenberg . . . . . .
5.6 Momenti magnetici associati ai moti orbitali elettronici .
5.7 Lo spin . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . .
dell’energia
. . . . . . .
. . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
21
21
24
27
28
29
32
32
Capitolo 1
Inquadramento storico
Verso la fine del XIX secolo la fisica aveva raggiunto un soddisfacente livello di sviluppo teorico e
sperimentale. Essa permetteva di rendere conto praticamente di tutti i fenomeni naturali allora conosciuti:
• La meccanica era stata completamente compresa e nella sua formulazione lagrangiana ed hamiltoniana aveva raggiunto un assoluto livello di rigore matematico.
• La derivazione delle quattro equazioni di Maxwell aveva, invece, riconciliato in un’unica teoria
di campo elettromagnetico tutta quella vastissima fenomenologia di effetti elettrici e magnetici
scoperta ed investigata negli ultimi cento anni.
• Parallelamente, l’ottica (sia geometrica che fisica) aveva spiegato tutti i principali fenomeni ondulatori (sia di tipo luminoso che meccanico).
• Infine, la termodinamica aveva permesso di capire in profondità le leggi che governano la generazione, lo scambio e la trasformazione di energia in forma di calore.
Cosa importantissima, le conoscenze teoriche avevano una vivace controparte sperimentale che aveva
favorito, a sua volta, un impetuoso sviluppo tecnologico.
Questo quadro confortante era destinato ad essere sconvolto nel giro di pochissimi anni nella transizione tra i secoli XIX e XX. Stava, infatti, per offrirsi all’attenzione dei fisici una ricca serie di nuovi
fenomeni che sfuggivano ad ogni tentativo di interpretazione basato sulla meccanica, elettromagnetismo,
ottica o termodinamica classica. In un modo o nell’altro, essi risultarono tutti riconducibili alle proprietà
fisiche del mondo microscopico.
La risposta che la comunità internazionale dei fisici diede a questa sfida rappresentò probabilmente il momento di più grande fertilità intellettuale di questa disciplina scientifica. Essa, infatti, porterà
all’elaborazione della meccanica quantistica ed alla sua applicazione sistematica ai nuovi fenomeni. La
meccanica quantistica rappresenta lo strumento più efficace per spiegare in modo profondo e completo
i fenomeni naturali su scala microscopica. Questa rivoluzione rappresenta, inoltre, un esempio estremamente significativo di come il metodo scientifico è capace di superare e trasformare i propri postulati di
base.
In questo Dispensa vengono presentate e discusse alcune fenomenologie microscopiche che risultano
non spiegabili in base alla fisica classica. Verrà, quindi, introdotto il rivoluzionario concetto di quanto
di energia che sta alla base degli sviluppi teorici che hanno portato alla formalizzazione della meccanica
quantistica.
4
Capitolo 2
Il calore specifico dei gas e dei solidi
2.1
Teoria cinetica dei gas
La teoria cinetica dei gas predice le proprietà macroscopiche dei gas a partire dall’ipotesi che essi siano
formati da costituenti elementari quali atomi o molecole. L’idea chiave alla base della teoria consiste nella
rinuncia a calcolare esplicitamente in modo esatto le proprietà di particella singola (obiettivo praticamente
irrealizzabile, visto che una mole di sostanza contiene dell’ordine di 1023 atomi), ma piuttosto di ragionare
in termini di grandezze medie, ovvero di grandezze valutate come media sull’intera popolazione di atomi
costituenti il gas.
Per semplicità noi svilupperemo la teoria cinetica nel caso di un gas monoatomico ideale. In altre
parole, assumeremo che: (i) il sistema sia costituito da una sola specie chimica in forma atomica; (ii) siano
trascurabili le interazioni atomo–atomo. Ognuno di essi, dunque, si muoverà liberamente (cioè, in basi
alle leggi della meccanica classica, di moto rettilineo uniforme) fino a quando non urti occasionalmente
con un altro atomo, o con una delle pareti del recipiente contenente il gas. Quando ciò accade l’atomo
subirà un urto che, sempre per semplicità, considereremo perfettamente elastico. Ne risulta, dunque, un
moto casuale a zig–zag come quello schematicamente rappresentato in Fig.2.1.
Descrivere, come sopra suggerito, in media le proprietà di questo moto, equivale a sostituire il concetto
di traiettoria esatta di ogni singola particella con quello di libero cammino medio λ. Supponiamo che gli
atomi siano sfere di raggio d: due di essi si urteranno quando la loro distanza sarà pari a 2d. Possiamo,
quindi, descrivere il moto del generico atomo del gas come quello di una particella di dimensioni 2d che
si muove, con velocità media pari a v̄, contro un insieme di particelle fisse e puntuali. Il numero di urti
sperimentato nell’unità di tempo risulta pari a 4πd2 v̄n, dove n è il numero di atomi per unità di volume
(densità di particelle). Abbiamo, cioè, contato il numero di particelle contenute, nell’unità di tempo,
in un cilindro di raggio 2d ed altezza v̄. Secondo una definizione proposta originalmente da Maxwell, il
libero cammino medio λ della particella è pari a
λ=
spazio percorso per unità di tempo
v̄
1
=
=
numero urti per unità di tempo
4πd2 v̄n
4πd2 n
.
(2.1)
Questa espressione, che quantifica in media il moto di una particella di un gas, è in accordo con il senso
comune: più denso è il materiale (maggiore è la sua densità n), minore è il libero cammino medio delle
sue particelle costituenti. Ugualmente: maggiore è la dimensione atomica d, minore risulta λ.
Consideriamo, dunque, un’assemblea di N atomi contenuta entro un recipiente cubico di lato l disposto, rispetto agli assi cartesiani, come indicato in Fig.2.2. Sia v il vettore che rappresenta la velocità di
un certo atomo, di componenti vx , vy e vz . Quando esso urta contro la parete posta a x = l subirà, come
detto, un urto elastico che non altera le componenti y ed z della velocità, mentre fa variare la componente
x dal valore iniziale vx al valore finale −vx . In altre parole, l’atomo varia la sua quantità di moto (o
momento lineare) di un valore pari a 2mvx , essendo m la sua massa. Tra questo urto ed il successivo contro questa stessa parete - deve passare, in media, un tempo pari a 2l/vx (questo, infatti, è il tempo
necessario per attraversare l’intero recipente da x = l ad x = 0 e tornare indietro da x = 0 ad x = l).
Durante un certo intervallo di tempo ∆t si osserveranno dunque un numero di urti contro la parete
pari a ∆t/(2l/vx ) in modo tale che la corrispondente variazione di quantità di moto risulta pari a
variazione totale quantità di moto = (numero urti) × (variazione quantità di moto per urto)
5
(2.2)
CAPITOLO 2. IL CALORE SPECIFICO DEI GAS E DEI SOLIDI
6
Figura 2.1: Rappresentazione schematica del moto casuale di un atomo secondo la teoria cinetica dei gas.
Figura 2.2: Cinematica del singolo urto elastico atomo–parete.
ovvero:
mvx2
∆t × (2mvx ) =
∆t .
(2.3)
2l
l
Secondo la meccanica classica, possiamo uguagliare tale variazione di quantità di moto all’impulso che la
particella ha esercitato in quell’intervallo di tempo sulla parete1 e scrivere
variazione totale quantità di moto =
fx ∆t =
v
x
mvx2
∆t
l
(2.4)
da cui ricaviamo il valore medio della forza fx esercitata dall’atomo sulla parete:
fx =
mvx2
l
.
(2.5)
Questo ragionamento può essere esteso alle altre due componeti cartesiane (ovvero agli urti contro le
pareti y = l e z = l) ed a tutte le altre particelle costituenti il gas, in modo che la forza totale media F
esercitata sulle pareti sarà:
PN 2
Fx
= ml
vx,i
Pi=1
N
m
2
Fy
= l
i=1 vy,i
P
N
2
.
(2.6)
Fz = ml
i=1 vz,i
Se il gas è all’equilibrio non ci sono differenze macroscopiche tra le tre componenti cartesiane della forza
totale e, quindi, possiamo calcolare la pressione P su una qualunque delle facce del recipiente cubico:
P =
1 Ricordiamo
Fx
Fy
Fx
= 2 = 2
l2
l
l
.
che l’impulso di una forza F che agisce per un tempo ∆t è semplicemente il prodotto F∆t
(2.7)
CAPITOLO 2. IL CALORE SPECIFICO DEI GAS E DEI SOLIDI
7
Possiamo, inoltre, scrivere che in media:
2
2
2
vx,i
= vy,i
= vz,i
=
1 2
v̄
3
(2.8)
per ogni particella i del gas, dove abbiamo introdotto la grandezza velocità quadratica media
v̄ 2 =
N
1 X 2
v
N i=1 i
(2.9)
2
2
2
dove vi2 = vx,i
+vy,i
+vz,i
rappresenta il modulo quadro della velocità della i–esima particella. Finalmente,
combinando le espressioni appena derivate, possiamo scrivere che la pressione vale
P =
1 m 2
N v̄
3 l3
(2.10)
ovvero
1
N mv̄ 2
3
dove abbiamo fatto uso del fatto che per il recipiente considerato V = l3 .
PV =
2.2
(2.11)
Energia interna di un gas monoatomico ideale ed equipartizione dell’energia
Consideriamo, ora, una mole di gas in modo che N = NA = 6.022 × 1023 sia il numero di Avogadro e,
quindi, il prodotto M = NA m rappresenti la massa di una mole. Ricordando l’equazione di stato dei gas
perfetti P V = RT (dove la costante universale dei gas R vale R = 8.314 J/K) possiamo scrivere
PV =
1
M v̄ 2 = RT
3
(2.12)
dove T è la temperatura del gas. Ne segue immediatamente una relazione di fondamenale importanza:
r
3RT
v̄ =
.
(2.13)
M
Essa sancisce, a meno di costanti, l’equivalenza tra la grandezza fisica macroscopica temperatura (quella
grandezza legata alla esperienza fisiologica del “caldo” e “freddo”) ed una grandezza fisica che descrive
una proprietà microscopica dei costituenti elementari della materia: la velocità quadratica media degli
atomi. Abbiamo, quindi, attribuito un chiaro significato fisico al concetto empirico di caldo e freddo: più
veloce è il moto di agitazione termica a livello atomico, maggiore è la temperatura del corpo. In modo
più quantitativo, possiamo legare l’energia cinetica media degli atomi alla temperatura:
1
3 R
3
mv̄ 2 =
T = KB T
2
2 NA
2
(2.14)
avendo introdotto la costante di Boltzmann
KB =
R
= 1.3807 × 10−23 J/K
NA
(2.15)
Osserviamo che questa relazione è valida all’equilibrio termodinamico quando, cioè, sia possibile definire
la temperatura di un sistema. Per esempio, se consideriamo un gas formato da idrogeno o da ossigeno
√
alla temperatura di 273 Kelvin (cioè allo zero gradi Celsius) otteniamo dei valori di velocità medie v̄ 2
pari a 1840 ms−1 e 460 ms−1 , rispettivamente.
Torniamo a considerare la generica particella del gas libera di muoversi nello spazio. Possiamo affermare che essa possiede tre gradi di libertà. La particella, infatti, ha una componente di moto per ciascuno
dei tre assi cartesiani. In modo alternativo, si può dire che una siffatta particella ha tre gradi di libertà
perchè ci vogliono tre coordinate cartesiane per definire in modo univoco la sua posizione nello spazio.
La eq.(2.14) stabilisce un risultato importantissimo: dato un gas monoatomico ideale all’equilibrio termodinamico alla temperatura T , ad ogni sua particella compete, in media, una energia pari a 12 KB T per
CAPITOLO 2. IL CALORE SPECIFICO DEI GAS E DEI SOLIDI
8
Figura 2.3: Legge di distribuzione delle velocità molecolari per un gas di ossigeno a T=80K e T=800K.
ogni grado di libertà. Questo risultato costituisce una prima (elementare) formulazione del principio di
equipartizione dell’energia. In base a questo principio, è immediato scrivere l’espressione per l’energia
interna U di una mole di gas monoatomico ideale2 :
U=
3
RT.
2
(2.16)
Sulla base di questi risultati, è possibile sviluppare un calcolo che permetta di ricavare la legge di
distribuzione delle velocità molecolari di una gas all’equilibrio termico. Con questo intendiamo una legge
capace di prevedere il numero Nv di particelle di un dato gas (all’equilibrio termico alla temperatura T )
che possiedono velocità compresa, in modulo, tra v e v+dv. Per brevità noi ricorderemo solo il risultato
finale che è dovuto a Maxwell:
32
m
mv 2
Nv = 4πN
v 2 exp −
(2.17)
2πKB T
2KB T
dove N è il numero totale di particelle formanti il gas. È importante ricordare che questa legge, riportata
in forma grafica in Fig.2.3, è stata verificata sperimentalmente in modo molto accurato. Questo risultato
costituisce una delle più convincenti prove di validità della teoria cinetica dei gas.
2.3
Calori specifici di gas mono– e bi–atomici
Ricordiamo che, secondo la termodinamica classica, il calore specifico di una certa sostanza alla temperatura T rappresenta il calore che è necessario somministrare ad una massa unitaria di quella sostanza
per aumentare la sua temperatura di un grado Kelvin. Quando questo processo è eseguito in condizioni
di volume costante, si parla di calore specifico a volume costante CV . La quantità di calore scambiata Q,
la variazione di temperatura ∆T ed il calore specifico sono legati dalla semplice relazione:
Q = CV ∆T
.
(2.18)
La termodinamica, poi, ci insegna che il calore scambiato Q tra un sistema e l’ambiente esterno, il
lavoro prodotto dal sistema W e la variazione della sua energia interna ∆U sono legati dalla relazione
Q = W + ∆U
(2.19)
nota come primo principio della termodinamica. Esso, in sostanza, sancisce la conservazione dell’energia
per processi termodinamici e può essere postulato su base sperimentale. Il modo più semplice per illustrarlo consiste nel considerare un gas contenuto in un recipiente a pareti fisse, sormontato da un pistone
mobile, come illustrato in Fig.2.4. Somministrando del calore Q al gas, esso: (i) si scalda o, equivalentemente, aumenta la sua energia interna secondo la eq.(2.16); (ii) scaldandosi, si espande muovendo
2 L’energia interna, infatti, è solo di tipo cinetico, essendo il gas ideale caratterizzato dalla assoluta assenza di energie
potenziali di interazione atomo–atomo.
CAPITOLO 2. IL CALORE SPECIFICO DEI GAS E DEI SOLIDI
9
Figura 2.4: Rappresentazione schematica del bilancio energetico tra calore, lavoro ed energia interna.
Figura 2.5: Rappresentazione dei due gradi di libertà rotazionali di una molecola biatomica rigida.
verso l’alto il pistone, cioè compiendo lavoro meccanico W . Se il pistone viene mantenuto fisso, non sarà
più possibile compiere lavoro esterno e, in base al primo principio della termodinamica, tutto il calore
assorbito dal sistema andrà in aumento di energia interna.
Questo fenomeno può essere quantificato in base ai risultati della teoria cinetica dei gas. Per una mole
di un gas monoatomico ideale, infatti, si ha che:
Q = CV ∆T = ∆U =
3
R∆T
2
(2.20)
da cui risulta immediatamente che
CV =
3
R
2
gas monoatomico ideale .
(2.21)
Questo risultato è in buon accordo con il dato sperimentale e la cosa va considerata come un ulteriore
lusinghiero successo della teoria cinetica dei gas, nonostante le drastiche approssimazioni che abbiamo
adottato per svilupparla analiticamente.
Proviamo, ora, ad estendere i risultati fino a qui ottenuti al caso di un gas biatomico. In questo
caso, i suoi costituenti elementari sono molecole biatomiche formate da due atomi legati chimicamente.
Cominciamo col considerare queste molecole biatomiche come entità rigide. In altre parole, assumiamo
che i due atomi rimangano ad una distanza fissa. Un tale oggetto può, ovviamente, traslare nello spazio.
Possiederà, quindi, 3 gradi di libertà traslazionali. Inoltre, la molecola biatomica può ruotare attorno alle
due direzioni perpendicolari al suo asse molecolare, come illustrato in Fig.2.5.
Dovremo, cosı̀ aggiungere due gradi di libertà rotazionali, che portano ad un totale di 5 gradi di libertà
complessivi per molecola. In base al principio di equipartizione dell’energia, all’equilibrio termodinamico
alla temperatura T ogni molecola possiederà in media una energia pari a 25 KB T e, quindi, il calore
CAPITOLO 2. IL CALORE SPECIFICO DEI GAS E DEI SOLIDI
10
Figura 2.6: Andamento del calore specifico CV a volume costante per il gas biatomico H2 in funzione
della temperatura, riportata in ascissa in scala logaritmica.
specifico a volume costante risulterà essere
CV =
5
R
2
gas biatomico (molecole rigide) .
(2.22)
Questa volta l’accordo con i dati sperimentali è insoddisfacente. I valori misurati di CV , infatti, approssimano quello teorico soltanto in un limitato intervallo di temperature. La situazione è illustrata in
Fig.2.6.
Appare evidente che la predizione teorica risulta questa volta inadeguata sia alle basse, che alle alte
temperature. In particolare si osserva che:
• alle basse temperature il gas biatomico sembra comportarsi come un gas monoatomico; in altre
parole, sembra che i gradi di libertà rotazionali siano stati “congelati” e che non debbano essere
inclusi nella applicazione del principio di equipartizione dell’energia;
• alle alte temperature il gas biatomico sembra acquisire due nuovi gradi di libertà che portano il
valore di CV a 72 R.
L’unico modo possibile per riconciliare teoria cinetica e dato sperimentale è ammettere che al progressivo
aumentare della temperatura, vengano “accesi” sempre più gradi di libertà. Alle basse temperature, la
molecola è animata solo da moto traslatorio; a temperature intermedie vengono innescati anche i modi di
rotazione; infine, alle alte temperature i due atomi non possono più essere considerati fissi, ma acquistano
ciascuno un grado di libertà vibrazionale lungo l’asse molecolare3 . In altre parole, cioè, la molecola non
può più essere vista come una unità rigida. Questa interpretazione trova solo una giustificazione euristica;
non vi è modo di spiegare, tuttavia, il perchè debba esistere una tale dipendenza dalla temperatura del
numero e tipo di gradi di libertà molecolari attivi. Questa difficoltà rappresenta il primo importante
fallimento della teoria cinetica dei gas.
2.4
Calori specifici dei solidi
Da un punto di vista strutturale, possiamo descrivere un solido come una distribuzione ordinata e periodica di atomi. L’insieme di posizioni nello spazio occupate dagli atomi viene chiamato reticolo cristallino.
Per esempio, in Fig.2.7 vengono riportati tre diversi modi di realizzare strutture cristalline a simmetria
cubica.
La differenza fondamentale tra un solido ed un gas è che, mentre in quest’ultimo gli atomi (o molecole)
sono liberi di muoversi nello spazio, in un solido (per temperature inferiori a quella di fusione) gli atomi
sono vincolati ai siti reticolari. Essi, al più, possono oscillare attorno alla loro posizione di equilibrio, con
ampiezza variabile in funzione della temperatura. Affinchè, tuttavia, un atomo possa essere confinato
3 Questo modo di giustificare i due nuovi gradi di libertà vibrazionali non è rigoroso, come verrà discusso più avanti a
proposito del calore specifico dei solidi. Tuttavia esso rappresenta un semplice ed efficace modo per visualizzare il fenomeno
dell’“accesione” dei moti di vibrazione molecolare.
CAPITOLO 2. IL CALORE SPECIFICO DEI GAS E DEI SOLIDI
11
Figura 2.7: Celle convenzionali per il cristallo cubico semplice (sinistra), cubico a corpo centrato (centro)
e cubico a facce centrate (destra). I pallini neri rappresentano i siti reticolari, cioè le posizioni degli
atomi. Replicando periodicamente lungo i tre assi cartesiani queste celle convenzionali si ottiene il reticolo
cristallino completo.
in prossimità di un sito anche a temperatura finita, è necessario che su di esso agisca un potenziale
“confinante”, ovvero che esista una forza di richiamo che impedisca all’atomo il definitivo allontanamento.
È chiaro, dunque, che nel caso di un solido non potremo applicare banalmente la teoria cinetica del gas
ideale dove, invece, si erano escluse a priori azioni di forza su/tra gli atomi.
Per poter procedere, abbiamo bisogno di specificare la natura del potenziale “confinante” che ciascun
atomo di un solido sperimenta. Un ottimo modello approssimato (che risulta efficace nel descrivere
moltissime proprietà della materia allo stato solido) consiste nell’assumere che ogni atomo oscilli sul
fondo di una buca di potenziale di tipo armonico. In altre parole, possiamo assumere che ogni atomo sia
vincolato alla propria posizione di equilibrio da un potenziale elastico di tipo armonico. Ciò equivale ad
ammettere l’esistenza di una forza di richiamo del tipo F = −kr, dove r rappresenta il vettore spostamento
dal sito reticolare e k la costante elastica della “molla efficace” di richiamo all’equilibrio. Poichè ciascun
atomo può oscillare nelle tre dimensioni, possiamo facilmente scrivere la sua energia totale ET :
ET =
1
1
1
1
1
1
mv 2 + mv 2 + mv 2 + kx2 + ky 2 + kz 2
2 x 2 y 2 z 2
2
2
(2.23)
avendo, per semplicità, assunto che la costante di forza k sia la stessa nelle tre direzioni e che il vettore
spostamento r abbia componenti (x, y, z).
Figura 2.8: Confronto tra la legge di Dulong e Petit (curva sottile) ed i dati sperimentali (curva spessa)
per il calore specifico a volume costante di un solido di argento.
La differenza fondamentale tra un atomo di un gas ideale e quello di un cristallo armonico consiste
nella presenza di tre contributi di energia potenziale elastica nell’energia totale di quest’ultimo. Notiamo, però, che esiste una caratteristica comune ai contributi cinetici e potenziali nell’espressione di
ET : entrambi sono quadratici. I termini cinetici, infatti, dipendono dal quadrato della velocità, mentre
quelli potenziali dal quadrato dello spostamento. Questa analogia formale ci consente di giustificare una
CAPITOLO 2. IL CALORE SPECIFICO DEI GAS E DEI SOLIDI
12
estensione importante del principio di equipartizione dell’energia: assumeremo che per un sistema all’equilibrio termodinamico alla temperatura T competa, in media, un’energia pari a 21 KB T ad ogni grado
di libertà che introduca un termine quadratico nelle posizioni o nelle velocità nell’espressione dell’energia
totale. Questa formulazione generale del principio può essere dimostrata rigorosamente con i metodi della
meccanica statistica.
Considerando un solido costituito da N atomi e supponendo che sia all’equilibrio alla temperatura T
possiamo immediatamente scrivere la sua energia interna come U = 3N KB T e, per una mole di sostanza
(cioè N = NA ), ricavare il calore specifico:
CV = 3R
solido cristallino armonico .
(2.24)
Questo risultato è noto come legge di Dulong e Petit ed è verificato in buona approssimazione da moltissimi
solidi a temperature sufficientemente alte. Quando, tuttavia, si scende in temperatura, le risultanze
sperimentali evidenziano forti deviazioni dalla legge di Dulong e Petit fino a dimostrare che CV si annulla
alla temperatura zero. Questo risultato è illustrato in Fig.2.8.
L’incapacità di spiegare il calore specifico dei solidi costitisce un nuovo importante fallimento della
fisica classica. Per riconciliare teoria ed esperimento bisognerà, infatti, sostituire la descrizione di un
atomo cristallino come oscillatore classico, con quella più rigorosa di un oscillatore che obbedisce alle
regole della fisica quantistica.
Capitolo 3
Lo spettro del corpo nero
È esperienza comune che un corpo a temperatura sufficientemente alta irradia calore, facilmente percepibile anche senza strumenti sofisticati (si pensi al termosifone od alla stufa usati per riscaldamento
domestico). Questo fatto rappresenta una manifestazione del fenomeno dell’irraggiamento termico: ogni
corpo che si trovi ad una temperatura superiore allo zero assoluto emette radiazione elettromagnetica.
Tale radiazione (che, spesso, è indicata come radiazione termica per ricordare lo stretto legame con la
temperatura) è distribuita su tutto lo spettro delle frequenze (vedi Fig.3.1) e la sua intensità aumenta con
l’aumentare della temperatura. La distribuzione spettrale della radiazione termica manifesta un massimo
in corrispondenza di una frequenza νmax che aumenta all’aumentare della temperatura del corpo. Anche
questo fenomeno rientra nella nostra esperienza quotidiana: limitandosi, per esempio, a quella porzione
dello spettro elettromagnetico che corrisponde alla luce visibile (cioè a quella parte dello spettro che può
essere rilevata dall’occhio umano) è noto che scaldando sempre più un pezzo di metallo, il suo colore
passa dal rosso, all’arancio, al bianco. Il massimo di emissione di radiazione da parte del metallo avviene,
cioè, a frequenze sempre maggiori.
In generale, caratterizziamo la radiazione termica emessa da un corpo qualunque tramite il suo potere
emissivo spettrale eν (detto anche brillanza spettrale) che rappresenta la quantità di energia elettromagnetica emessa nell’unità di tempo dall’unità di superficie nell’intervallo di frequenze [ν, ν + dν]. Il potere
emissivo spettrale è legato da una semplice relazione alla densità di energia elettromagnetica uν emessa1 :
eν =
c
uν
4
(3.1)
dove c è la velocità della luce. Naturalmente, un corpo può anche assorbire radiazione elettromagnetica.
Possiamo quantificare il processo di assorbimento tramite il potere assorbente spettrale aν (o assorbanza
1 Ricordiamo che u rappresenta la quantità di energia elettromagnetica per unità di volume ed è proporzionale al modulo
ν
quadro del vettore campo elettrico ed al modulo quadro del vettore campo magnetico che definiscono l’onda elettromagnetica
di frequenza ν che stiamo considerando.
Figura 3.1: Lo spettro della radiazione elettromagnetica.
13
CAPITOLO 3. LO SPETTRO DEL CORPO NERO
14
Figura 3.2: Rappresentazione schematica di un corpo nero come cavità.
spettrale), definito come la quantità di energia elettromagnetica assorbita nell’unità di tempo dall’unità
di superficie nell’intervallo di frequenze [ν, ν + dν]. È naturale aspettarsi che eν ed aν dipendano, presi
singolarmente, dalla natura chimico–fisica del corpo che stiamo considerando (un pezzo di metallo esposto
all’irraggiamento solare si scalda diversamente da un pezzo di plastica) e dalle caratteristiche della sua
superficie (un corpo di superficie lucida assorbe meno radiazione di un corpo uguale, ma con superficie
opaca). Tuttavia è possibile dimostrare che, per ogni fissata frequenza ν, il loro rapporto è una funzione
universale della sola temperatura. In altre parole, vale la seguente legge di Kirchhoff
Σν (T ) =
eν
aν
(3.2)
dove Σν (T ) rappresenta tale funzione universale, che non dipenderà più in alcun modo dallo specifico
corpo considerato, ma solo dalla sua temperatura.
È utile introdurre a questo punto il concetto di corpo nero, come quel corpo capace di assorbire tutta la
radiazione elettromagnatica su di esso incidente, per qualunque frequenza e per qualunque temperatura.
In altre parole, un corpo nero è un oggetto che non riflette (nè trasmette) radiazione. Il concetto di
corpo nero è un’astrazione, ma possiamo citare diversi esempi pratici in cui un oggetto si comporta quasi
esattamente come un corpo nero. Si pensi, ad esempio, ad una cavità ricavata dentro ad un oggetto come
rappresentata in Fig.3.2. La radiazione elettromagnetica può penetrare entro la cavità (caratterizzata da
pareti riflettenti) attraverso una piccola apertura. Una volta entrata nella cavità, la radiazione rimane
ivi “intrappolata”, perchè è molto poco probabile che riesca a fuoriscire attraverso la piccola fenditura.
In altre parole, la cavità assorbe praticamente tutta la radiazione che riceve. È, quindi, un corpo nero a
tutti gli effetti pratici.
Segue immediatamente dalla definizione data che un corpo nero ha potere assorbente spettrale unitario
a qualunque frequenza: aν (corpo nero)=1. La legge di Kirchhoff, dunque, può essere interpretata come
segue: il rapporto tra potere emissivo e potere assorbente di un corpo qualsiasi ad un certa frequenza
e temperatura è sempre uguale al potere emissivo del corpo nero a quella frequenza e temperatura.
Da questa semplice deduzione, discende l’enorme importanza concettuale che ha il corpo nero per quel
capitolo della fisica che si occupa di termodinamica della radiazione. Se conosciamo lo spettro di emissione
del corpo nero, siamo in grado di risalire, tramite la legge di Kirchhoff, alle caratteristiche di assorbimento
ed emissione di un qualsiasi altro oggetto. Per questo motivo, il corpo nero fu dettagliatamente studiato
negli ultimi tre decenni del XIX secolo.
3.1
Gli esperimenti e la teoria classica
Il tipico apparato sperimentale per lo studio dello spettro di emissione del corpo nero è schematicamente
rappresentato in Fig.3.3: la cavità C rappresenta il corpo nero le cui pareti vengono portate alla temperatura desiderata tramite accoppiamento con il termostato T . La materia che forma queste pareti emette
radiazione termica che rimane intrappolata nella cavità2 . Se pratichiamo un orefizio O attraverso una
2 Più rigorosamente, diremo che la radiazione emessa dalle pareti della cavità rimane ivi confinata dando origine ad un
sistema di onde elettromagnetiche stazionarie.
CAPITOLO 3. LO SPETTRO DEL CORPO NERO
15
Figura 3.3: Apparato sperimentale per la rivelazione dello spettro di corpo nero.
Figura 3.4: Lo spettro di corpo nero raccolto sperimentalmente a diverse temperature (linee continue).
La linea tratteggiata rappresenta la legge classica di Rayleigh–Jeans.
parete, la radiazione termica può fuoriuscire, ovvero viene emesso lo spettro di corpo nero che è infine
raccolto ed analizzato (sia in intensità, che in distribuzione spettrale) dal rivelatore R.
Il risultato sperimentale è descritto in Fig.3.4 dove viene riportata la densità di energia elettromagnetica uν emessa da un corpo nero a diverse temperature, in funzione della frequenza ν. L’analisi
quantitativa delle curve sperimentali ha permesso di stabilire alcune leggi fenomenologiche:
• legge di Stefan (1879): l’energia elettromagnetica totale utot irraggiata per unità di tempo dall’unità
di area è proporzionale alla quarta potenza della temperatura T del corpo nero:
utot = σT 4
(3.3)
dove σ = 5.67 × 10−8 Wm−2 K−4 è detta costante di Stefan;
• legge di Wien (1893): la frequenza νmax alla quale si ha il massimo della densità spettrale della
radiazione di corpo nero dipende in modo direttamente proporzionale dalla temperatura:
νmax
= costante
T
(3.4)
(questa legge è anche nota come legge dello spostamento).
Il tentativo classico di spiegazione di queste risultanze sperimentali e delle corrispondenti leggi fenomenologiche fu elaborato come segue. Quando la radiazione di corpo nero presente nella cavità è in
equilibrio termico con la materia che costituisce le pareti di quest’ultima, allora deve esserci corrispondenza tra la distribuzione di energia della radiazione e quella degli atomi che formano il materiale delle
CAPITOLO 3. LO SPETTRO DEL CORPO NERO
16
pareti3 . Calcoliamo, dunque, quella degli atomi che, essendo animati da moti di oscillazione termica, si
comportano in buona approssimazione come oscillatori armonici. Dalla meccanica classica sappiamo che
un oscillatore armonico di massa m, frequenza propria ν ed ampiezza di oscillazione R possiede energia
Eoscillatore
armonico classico
= 2π 2 mν 2 R2
,
(3.5)
ovvero può possedere qualunque valore continuo di energia (purchè la frequenza e l’ampiezza di oscillazione
abbiano valori opportuni). Classicamente, dunque, la radiazione di corpo nero è descritta come un insieme
di onde stazionarie confinate nella cavità con distribuzione continua di frequenze. È possibile calcolare
che il numero dnν di onde per unità di volume con frequenza compresa nell’intervallo [ν, ν + dν] è
8π 2
ν dν
(3.6)
c3
cui, alla temperatura T , corrisponde una energia media per unità di volume e per intervallo spettrale
[ν, ν + dν] pari a:
uν dν = Em dnν = KB T dnν
(3.7)
dnν =
dove abbiamo fatto uso del principio di equipartizione dell’energia, imponendo che l’energia media Em
degli oscillatori armonici valga all’equilibrio termico KB T . Segue immediatamente che per la densità di
energia uν vale la seguente espressione
8π
(3.8)
uν = 3 ν 2 KB T
c
nota come legge di Rayleigh–Jeans. Il confronto tra i risultati sperimentali ed il modello teorico che
abbiamo fin qui sviluppato è riassunto in Fig.3.4. Come si vede possiamo ritenere buono tale accordo
nel limite di piccole frequenze, mentre esso risulta assolutamente insoddisfacente alle alte frequenze. Il
modello di Rayleigh–Jeans, infatti, non prevede l’esistenza di un massimo per uν che, addirittura, cresce
in modo monotono fino a divergere per frequenze elevate. La conseguenza di ciò è importante: integrando
l’eq.(3.8) su tutto lo spettro, si ottiene un risultato infinito. Questo risultato paradossale fu chiamato
catastrofe ultravioletta per indicare il fallimento della teoria alle alte frequenze. Il risultato trovato è
particolarmente insoddisfacente perchè: (i) contrasta con il principio di conservazione dell’energia4 ; (ii)
non permette di spiegare la legge di Stefan; (iii) non consente di giustificare il valore numerico della
costante di Stefan σ.
In conclusione, la fisica classica non riesce a spiegare lo spettro di emissione di un corpo nero.
3.2
La teoria quantistica di Planck
L’enigma dello spettro di corpo nero fu risolto da Planck nel 1900 con l’introduzione di una ipotesi
rivoluzionaria. Planck, infatti, assunse che ciascun oscillatore armonico radiativo potesse emettere (e,
equivalentemente, assorbire) energia solo in quantità proporzionali alla sua frequenza ν. Questa ipotesi
corrisponde ad ammettere che l’energia di un oscillatore atomico sia quantizzata5 . Questa condizione
è in totale discontinuità con la teoria elettromagnetica classica che, invece, prevede che energia emessa (o assorbita) e frequenza di oscillazione siano direttamente proporzionali e variabili con continuità.
Operativamente, Planck sostituı̀ l’eq.(3.5) con la seguente espressione
Eoscillatore
armonico quantistico
= nhν
(3.9)
dove n = 1, 2, 3, · · · è un numero intero qualunque e h è una opportuna costante di proporzionalità il cui
valore deve essere ancora determinato.
Planck ripercorse il ragionamento che abbiamo già schematicamente sviluppato, utilizzando la nuova
espressione per l’energia di oscillatore. Il risultato ottenuto è rappresentato dalla espressione
uν =
ν3
8πh
c3 exp hν − 1
KB T
(3.10)
3 Se cosı̀ non fosse, si osserverebbe un flusso di energia tra parete e radiazione, o viceversa. Possiamo, perciò calcolare
indifferentemente la distribuzione di energia degli atomi o della radiazione, a seconda della nostra convenienza: le due
distribuzioni sono uguali in virtù di questo equilibrio.
4 Basterebbe scaldare un corpo nero ad una qualunque temperatura maggiore di zero per emettere una quantità infinita
di energia.
5 L’aggettivo quantizzata significa che tale energia non è più una funzione continua della frequenza, ma diventa una
grandezza discreta.
CAPITOLO 3. LO SPETTRO DEL CORPO NERO
17
nota come legge di Planck per il corpo nero. Questa formula è in ottimo accordo con i dati sperimentali
di Fig.3.4. Infatti:
• il limite per frequenze infinite è zero;
• il limite per frequenza nulla è zero;
• il limite per frequenze piccole è uν ∼ ν 2 , in accordo con la teoria di Rayleigh–Jeans;
• l-eq.(3.10) ammette un massimo per una certa frequenza νmax che dipende linearmente dalla
temperatura;
• il grafico dell’eq.(3.10) per ogni data temperatura è indistinguibile dalle curve sperimentali su tutto
lo spettro di frequenze.
Il valore di h, chiamata costante di Planck, fu ottenuta per calibrazione sulle curve sperimentali. Ad essa
è assegnato il valore numerico
h = 6.62 × 10−34 J s .
(3.11)
L’ipotesi di quantizzazione delle energie introdotta da Planck ebbe, nonostante il suo carattere rivoluzionario, grande eco in virtù dell’eccellente accordo teoria–esperimento che essa forniva. Essa fu
immediatamente adottata da Einstein per tentare di risolvere il problema ancora aperto del calore specifico dei solidi. Considerando, dunque, gli N atomi di un reticolo cristallino come oscillatori armonici
quantizzati tridimensionali, Einstein ricavò una nuova espressione per l’energia interna U di un solido,
ottenendo:
hν
solido cristallino armonico quantizzato .
(3.12)
U = 3N
exp Khν
−
1
BT
Nel caso di volume costante, il primo principio della termodinamica consente di scrivere6 per una
variazione finita ∆T di temperatura:
∆U
CV =
.
(3.13)
∆T
Estendendo questa espressione al caso di trasformazioni infinitesime a volume costante otteniamo immediatamente che

2
hν
dU
hν
 exp
KB T CV =
= 3R 
(3.14)
dT
KB T
exp Khν
−
1
BT
dove abbiamo considerato una mole di sostanza N = NA . Considerando questa nuova espressione per il
calore specifico di un solido, è facile dimostrare che:
• il limite per temperatura nulla è zero;
• il limite per temperatura infinita è 3R.
Inoltre, la rappresentazione grafica dell’eq.(3.14) riproduce quasi esattamente l’andamento sperimentale
di Fig.2.18 per tutti i materiali considerati7 .
6 Si
vedano le eq.(2.19) e (2.20), facendo uso del fatto che W = 0.
possibile migliorare ulteriormente l’accordo con il dato sperimentale, ammettendo che gli N atomi di un cristallo
possano oscillare a frequenze diverse. Esisteranno, quindi, per ciascun materiale considerato delle frequenze proprie di
oscillazione su ciascuna delle quali si può ripetere il ragionamento di Einstein, pervenendo ad una formula solo leggermente
diversa, ma in eccellente accordo con gli esperimenti. Il fatto che gli atomi di un cristallo possano oscillare a diverse
frequenze è conseguenza diretta delle loro interazioni reciproche. Questo miglioramento della teoria di Einstein fu dovuto
al fisico Debye.
7 È
Capitolo 4
L’effetto fotoelettrico
Discutiamo un altro effetto la cui interpretazione corretta è basata sull’ipotesi di quantizzazione dell’energia. Si consideri l’apparato sperimentale di Fig.4.1 dove due armature metalliche A (anodo) e C (catodo)
sono inserite in un tubo a vuoto T . Le due armature sono collegate ad un generatore di differenza di
potenziale V ed il circuito è completato da un misuratore di intensità di corrente elettrica G. In condizioni
normali, ovviamente, il misuratore G non registra il passaggio di alcuna corrente. Tuttavia, qualora il
catodo C venga illuminato da una radiazione elettromagnetica opportuna, si osserva passaggio di corrente
nel circuito. Questo fenomeno, scoperto ed analizzato in due fasi distinte da Hertz e da Hallwachs e
Lenard, fu chiamato effetto fotolelettrico.
La cosa importante da sottolineare in modo particolare è che si osserva passaggio di corrente solo se
la radiazione incidente ha frequenza opportuna. Per esempio, se le due armature C ed A sono di tipo
metallico, si osserva effetto fotoelettrico solo se la frequenza è maggiore od uguale a quella della luce
ultravioletta. Per frequenze inferiori, non si osserverà mai il fenomeno, neanche aumentando di molto
l’intensità della radiazione. In condizioni di opportuna illuminazione (cioè fissando la frequenza della
luce ad un valore opportuno), si osserva tra anodo e catodo una corrente elettrica i il cui andamento in
funzione della differenza di potenziale V tra C ed A è illustrato in Fig.4.2. Questa curva sperimentale ha
alcune caratteristiche importanti:
• i è diversa da zero anche quando V = 0;
• i satura ad un valore massimo, oltre il quale non si riesce ad andare, neanche aumentando arbitrariamente la differenza di potenziale;
• esiste un valore di differenza di potenziale negativo (cioè corrispondende ad una situazione di
inversione di polarità della V) in corrispondenza del quale i si annulla;
• mantenendo la frequenza della luce costante ad un valore opportuno, ma aumentando l’intensità
della stessa, la corrente satura ad un valore di intensità maggiore.
Figura 4.1: Schema dell’apparato sperimentale per l’osservazione dell’effetto fotoelettrico.
18
CAPITOLO 4. L’EFFETTO FOTOELETTRICO
19
Figura 4.2: Andamento sperimentale della corrente i prodotta per effetto fotoelettrico in funzione della
d.d.p. erogata dal generatore V.
L’interpretazione teorica dell’effetto fotoelettrico fu offerta per la prima volta da Einstein nel 1905.
Innanzitutto va osservato che affinchè circoli corrente nel circuito di Fig.4.1 è necessario ammettere che
dei portatori di carica (elettroni, in questo caso) siano emessi da catodo. Essi, accelerati dalla tensione
generata da V, verranno raccolti sull’anodo e, quindi, rilevati da G. Bisogna, quindi, ammettere che
la radiazione elettromagnetica abbia, in opportune conduzioni, la capacità di estrarre elettroni dalla
superficie metallica del catodo. Einstein, utilizzando il concetto di quantizzazione di Planck, ipotizzò
che una radiazione di frequenza ν fosse rappresentabile come pacchetti di luce, ciascuno avente energia
pari a hν. Questi pacchetti furono chiamati fotoni o quanti di luce. In altre parole Einstein sostituı̀
la descrizione tradizionale della luce come fenomeno ondulatorio, con una descrizione corpuscolare: un
raggio luminoso di frequenza ν è un flusso di fotoni di energia hν. Ciascun fotone incidente sul catodo
può interagire con gli elettroni di conduzione e trasmettere ad uno di essi tutta la sua energia. In altre
parole, il meccanismo di interazione radiazione–materia tra luce e catodo è descritto come una serie di
interazioni tra corpuscoli (elettroni e fotoni) che scambiano energia1 .
Un elettrone che acquista energia hν da un fotone fuoriesce dalla superficie metallica solo se la sua
energia cinetica Ecin è maggiore o al più uguale al lavoro di estrazione W del metallo. Ricordiamo che il
lavoro di estrazione di un metallo rappresenta la minima quantità di energia che è necessario trasmettere
ad un elettrone immerso in un metallo affinchè venga rotto il suo legame col metallo stesso. Questa
grandezza assume un valore caratteristico tipico per ciascun metallo. Tipicamente W ha il valore di
alcuni elettronVolt (eV) per i metalli più noti. Ricordiamo che l’elettronVolt rappresenta una unità di
misura di energia definita cosı̀ : 1 eV è l’energia cinetica acquistata da un elettrone accelerato da una
differenza di potenziale pari ad 1 Volt. Quindi, poichè si ha che
Ecin = hν − W
(4.1)
la condizione sotto la quale si osserva estrazione di elettroni, ovvero si misura corrente nel circuito, risulta
essere:
hν > W .
(4.2)
L’ipotesi di esistenza del fotone spiega, quindi, in modo naturale perchè la manifestazione dell’effetto
fotoelettrico dipenda dalla frequenza della radiazione usata. Possiamo, poi, aggiungere una stima quantitativa per la cosidetta frequenza di soglia ν0 al di sotto della quale non si osserverà mai fotoemissione
di elettroni:
W
(4.3)
ν0 =
h
che corrisponde, per i metalli, ad una frequenza ultravioletta.
1 L’ipotesi di Einstein, che gli valse il premio Nobel per la fisica, anticipò il concetto di dualismo onda–corpuscolo che
sottointende tutta la fisica quantistica. Secondo questo concetto, ogni fenomeno naturale può efficacemente essere descritto
come un’onda o come un corpuscolo, a seconda della specifica situazione considerata. Esistono, poi, precise regole di
corrispondenza tra la natura ondulatoria e corpuscolare dello stesso fenomeno o oggetto. La luce, quindi, è descritta in
modo impeccabile come un’onda quando se ne considerino le modalità di propagazione, riflessione, rifrazione, interferenza.
In modo parimenti efficace e veritiero, la luce è descrivibile come un flusso di corpuscoli, i fotoni, quando interagisce con
l’insieme degli elettroni di un cristallo.
CAPITOLO 4. L’EFFETTO FOTOELETTRICO
20
Figura 4.3: Analisi grafica qualitativa delle traiettorie degli elettroni fotoemessi dal catodo ed accelerati
dal campo elettrico esistente tra catodo ed anodo.
L’ipotesi di Einstein consente anche di spiegare l’andamento della corrente in funzione della tensione
applicata. Il generico elettrone fotoemesso fuoriesce dalla superficie del catodo con una vettore velocità
orientato a caso. Tale velocità iniziale, quindi, possiede una componente orizzontale ed una verticale.
Poichè tra le due armature esiste un campo elettrico costante ed uniforme, l’elettrone subisce l’azione di
una forza costante diretta orizzontalmente, cosı̀ come indicato in Fig.4.3. Il moto risultante è descritto da
un arco di parabola, la cui curvatura dipende dal modulo e dalla direzione della velocità iniziale dell’elettrone fotoemesso, cosı̀ come dal valore della differenza di potenziale elettrostatico applicata tra catodo ed
anodo. In generale, non tutte le traiettorie hanno una curvatura tale per cui l’elettrone possa venire raccolto sull’anodo. Tuttavia, se aumentiamo la differenza di potenziale, riusciremo a curvare sempre più le
traiettorie, fino a raggiungere il valore in corrispondenza del quale tutti gli elettroni fotoemessi dal catodo
vengono raccolti sull’anodo: questa condizione corrisponde alla condizione di corrente di saturazione.
Al contrario, se invertiamo la polarità del generatore V, otteniamo l’effetto di curvare le traiettore
degli elettroni emessi in direzione opposta, cioè faremo deflettere gli elettroni uscenti verso il catodo.
Quando la differenza di potenziale negativa raggiunge un certo valore, allora tutti gli elettroni emessi
tornano sul catodo e la corrente si annulla. Questo valore di differenza di potenziale negativa si chiama
potenziale di arresto Varresto .
Infine, i diversi valori di corrente di saturazione che si osservano al variare della intensità della radiazione, sono anch’essi spiegabili in base a questa interpretazione corpuscolare della luce. Aumentare
l’intensità di un fascio luminoso, infatti, significa aumentare il numero di fotoni contenuti nel fascio.
Un fascio più intenso (di opportuna frequenza), dunque, depositerà un maggior numero di fotoni sulla
superficie del catodo e conseguentemente farà emettere un maggior numero di elettroni. Ciò equivale a
raggiungere correnti di maggior intensità.
In conclusione, possiamo affermare che per la terza volta (calori specifici, spettro del corpo nero ed
effetto fotoelettrico) l’introduzione di una ipotesi di quantizzazione ha riconciliato i dati sperimentali con
l’interpretazione teorica. Appare, quindi, evidente che le leggi della Natura sulla scala microscopica non
possono più essere quelle della fisica classica, cui è estraneo ogni concetto di discretizzazione (quantizzazione). Fino ad ora, tuttavia, il concetto di quanto è stato introdotto per pura convenienza, senza
alcuna giustificazione formale, se non quella euristica: cosı̀ facendo si mettono a posto le cose ... Appare
evidente, quindi, la necessità di sviluppare un nuovo capitolo della fisica dove i fenomeni di quantizzazione
risultino come naturale conseguenza dei principi di base.
Capitolo 5
La fisica dei quanti
Questo Capitolo si apre con la discussione di una nuova serie di risultanze sperimentali emerse agli inizi
del XX secolo a riguardo degli spettri di emissione ed assorbimento di radiazione elettromagnetica da
parte di sistemi atomici. Ancora una volta, le misure risultarono sconcertanti perchè non giustificabili
classicamente.
La prima risposta organica al nuovo enigma fu elaborata da Bohr e condusse alla formulazione del
primo modello teorico per la struttura dell’atomo, descritto nel secondo e terzo paragrafo di questo
Capitolo. La teoria di Bohr ha la notevole caratteristica di essere fondata su una ipotesi di partenza di
tipo quantistico.
Il Capitolo termina con la discussione del concetto di dualismo onda–corpuscolo, concetto che sta alla
base della moderna teoria quantistica.
5.1
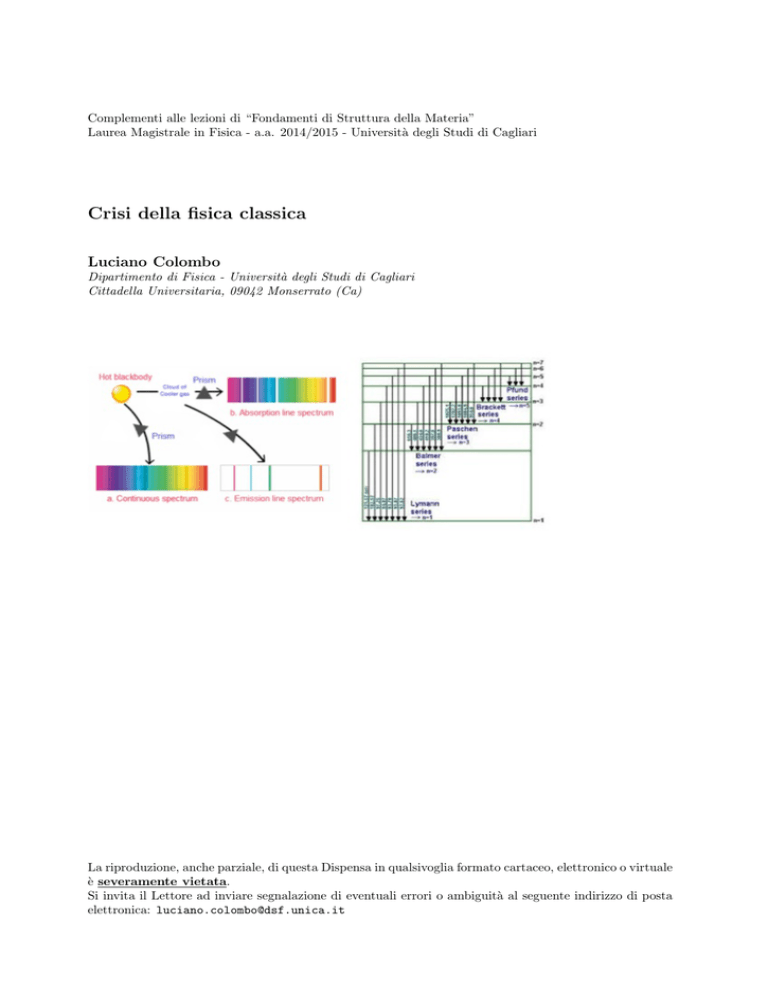
Spettri atomici
Riferiamoci, per semplicità, all’atomo di idrogeno che, come noto, è formato da un elettrone legato ad
un nucleo formato da un solo protone. Se si misura sperimentalmente la frequenza della radiazione
elettromagnetica emessa da questo atomo, si ottiene il risultato rappresentato in Fig.5.1 da cui si evince
una cosa importantissima: la radiazione emessa da un atomo possiede solamente alcune lunghezze d’onda
determinate (o, analogalmente, alcune frequenze determinate). In altre parole, lo spettro di emissione è
discreto. Tali lunghezze d’onda si raggruppano inoltre in sequenze di righe. Più in dettaglio, possiamo
dire che le diverse righe spettrali si raggruppano in sequenze regolari chiamate serie. Le lunghezze d’onda
λ delle diverse righe formanti una serie soddisfano la seguente regola empirica scoperta da Rydberg:
1
1
1
=R
− 2
(5.1)
λ
n21
n2
dove la costante R (costante di Rydberg) vale 109677 cm−1 . I numeri n1 ed n2 sono numeri interi positivi
che individuano le diverse serie secondo le seguenti relazioni
n1
n1
n1
n1
n1
=1
=2
=3
=4
=5
e
e
e
e
e
n2
n2
n2
n2
n2
= 2, 3, 4, · · ·
= 3, 4, 5, · · ·
= 4, 5, 6, · · ·
= 5, 6, 7, · · ·
= 6, 7, 8, · · ·
serie
serie
serie
serie
serie
di
di
di
di
di
Lyman
Balmer
Paschen
Brackett
Pfund ;
(5.2)
le serie hanno preso il nome dallo sperimentatore che per primo le ha risolte spettroscopicamente. È
importante notare che gli spettri di assorbimento presentano esattamente le stesse caratteristiche. La
radiazione elettromagnetica è anch’essa assorbita da un atomo di idrogeno (o da un qualunque altro atomo) a lunghezze d’onda date dalla legge di Rydberg. Le lunghezze d’onda (e le frequenze) di
assorbimento/emissione sono esattamente coincidenti.
L’interpretazione delle misure sperimentali sugli spettri atomici richiede l’utilizzo di un adeguato
modello di struttura atomica. L’ipotesi allora più accreditata era basata sul modello atomico di Thomson, secondo il quale un atomo all’equilibrio è formato da una distribuzione continua di carica elettrica
21
CAPITOLO 5. LA FISICA DEI QUANTI
22
Figura 5.1: Spettro di emissione/assorbimento dell’atomo di idrogeno.
Figura 5.2: Traiettorie di diffusione di particelle α come osservate nell’esperimento di Rutherford.
positiva1 nella quale sono presenti delle cariche elettriche negative puntiformi (gli elettroni) in numero
sufficiente ad assicurare la neutralità di carica dell’atomo nel suo complesso. Era stato però dimostrato da
Earnshaw che, in base alla elettrostatica classica, una siffatta distribuzione di cariche positive e negative
compenetrantesi non è stabile. Inoltre, questa struttura atomica non era compatibile con le risultanze
spettroscopiche.
Il modello di Thomson fu sostituito dal modello planetario di Rutherford, elaborato nel 1911 a seguito
di esperimenti di diffusione di un fascio di particelle α attraverso una sottile lamina metallica2 . L’analisi
delle traiettorie delle particelle diffuse dimostrava che si davano tre casi possibili, come indicato in Fig.5.2:
• alcune particelle venivano solo leggermente deviate durante l’ attraversamento della lamina (traiettoria 1);
• altre particelle invece venivano deviate fortemente rispetto alla traiettoria di avvicinamento (traiettoria 2);
• infine alcune particelle venivano addirittura retrodiffuse (traiettoria 3).
L’unica possibilità che spieghi quanto osservato consiste nell’ipotizzare che ogni atomo formante la
lamina metallica sia costituito da un nucleo massivo, caricato positivamente e praticamente puntiforme,
attorno al quale ruotino gli elettroni su orbite che, per semplicità, possiamo considerare perfettamente
circolari. Ne risulta il modello di atomo nucleare o planetario illustrato in Fig.5.3.
Riferendoci di nuovo all’atomo di idrogeno, l’intrepretazione degli spettri atomici nell’ambito del
modello di Rutherford passa attraverso il calcolo della radiazione emessa da un elettrone in orbita circolare
1 Per semplicità, possiamo immaginarla come una sfera carica con densità di carica spaziale data da una certa funzione
ρ(x, y, z).
2 Ricordiamo che una particella α è costituita dal nucleo di un atomo di elio; essa, quindi, è una particelle di carica
elettrica positiva.
CAPITOLO 5. LA FISICA DEI QUANTI
23
Figura 5.3: La struttura dell’atomo planetario (o nucleare) di Rutherford (sinistra). Giustificazione della
deviazione di traiettoria per una parlicella α nei tre casi descritti nel testo (destra).
attorno ad un nucleo e soggetto alla forza elettrostatica di attrazione data dalla legge di Coulomb:
Felettrone−nucleo = −
1 e2
4π0 r2
(5.3)
dove abbiamo indicato con e = 1.6 × 10−19 C la carica elettrica (positiva) del protone formante il nucleo
e dell’elettrone (negativa); r indica il raggio dell’orbita circolare percorsa da quest’ultimo durante il suo
moto di rivoluzione. Poichè l’eq.(5.3) rappresenta una forza radiale di tipo centrale, il moto dell’elettrone
sarà di tipo circolare uniforme, come studiato in meccanica classica. Se assumiamo (come indica la
chimica dell’atomo di idrogeno) che r=0.529 Å=0.529 ×10−8 cm, allora ne segue che i moduli della
velocità di rotazione v e della corrispondente accelerazione a valgono rispettivamente:
q
2
v = 4πe0 mr = 2.19 × 106 m s−1
a
=
v2
r
= 9.02 × 1022 m s−2
(5.4)
dove m = 9.11 × 10−31 Kg è la massa dell’elettrone. In generale, la potenza P irraggiata (cioè la quantità
di energia elettromagnetica emessa nell’unità di tempo) da una particella di carica e che si muove con
accelerazione a è data dalla espressione
e2 a2
P =
(5.5)
6π0 c3
nota come formula di Larmor3 . Sostituendo tutti i valori numerici noti, otteniamo che la potenza PH
irraggiata classicamente da un atomo di idrogeno vale
PH = 4.72 × 1011 eV s−1
.
(5.6)
Dalla chimica è noto come l’energia di ionizzazione di un atomo di idrogeno sia pari a 13.6 eV. In altre
parole, bisogna spendere un lavoro pari a 13.6 eV per strappare l’elettrone dal suo nucleo e portarlo a
distanza infinita. La quantità 13.6 eV rappresenta, dunque, la quantità di energia immagazzinata in un
atomo di idrogeno nello stato fondamentale sotto forma di interazione elettrostatica.
Se essa viene dissipata nel tempo secondo la potenza PH che abbiamo calcolato, allora un atomo di
idrogeno perde tutta la sua energia in un tempo dell’ordine di 10−11 s. Il risultato è stupefacente: secondo
la fisica classica, un atomo di idrogeno perde tutta la sua energia in poco più che un centomiliardesimo
di secondo. “Perdere energia” significa dire che l’elettrone diminuisce la sua velocità di rotazione e,
conseguentemente, vede diminuire il suo raggio orbitale. In una parola: secondo la fisica classica un
elettrone precipita sul nucleo in un tempo dell’ordine di 10−11 s. La materia, cosı̀ come noi la conosciamo,
non dovrebbe essere stabile!
Il quadro è già abbastanza sconfortante, ma, putroppo, le cose vanno ancor peggio di cosı̀İnfatti, un
elettrone che irraggia e, quindi, rallenta cadendo sul nucleo, si muove di un moto a spirale, piuttosto
3 Questa equazione è ricavata esplicitamente nel libro R. Mazzoldi, M. Nigro e C. Voci, “Fisica - vol.
Elettromagnetismo ed onde” (casa editrice EdiSES).
II -
CAPITOLO 5. LA FISICA DEI QUANTI
24
Figura 5.4: Traiettoria a spirale seguita da un elettrone in orbita attorno al nucleo atomico secondo la
fisica classica.
complicato, ma schematicamente illustrato in Fig.5.4. Durante questo moto, il suo raggio r(t) varia
1
nel tempo con continuità secondo una legge del tipo: r(t) = r0 − At 3 , con r0 pari al valore iniziale
della distanza elettrone–nucleo e A costante opportuna. Durante questo moto di rivoluzione, l’elettrone
dovrebbe emettere radiazione elettromagnetica con frequenza variabile con continuità. In altre parole:
classicamente gli spettri dovrebbero essere continui.
Il punto cui siamo arrivati è sconsolante: secondo la fisica classica gli atomi (e dunque la materia) non
dovrebbero essere stabili e dovrebbero emettere spettri continui. Invece, la materia esiste stabilmente
e gli spetri atomici sono discreti. C’è qualcosa di qualitativamente sbagliato nel modello atomico che fu
sviluppato da Rutherford.
5.2
Il modello di Bohr per l’atomo di idrogeno
L’impasse cui si era pervenuti, indusse Bohr a formulare nel 1913 un modello per l’atomo di idrogeno
basato su due postulati nei quali il concetto di discretizzazione (quantizzazione) delle frequenze veniva
introdotto fin da subito. Questo modello è costruito su due postulati.
In base al primo postulato Bohr assunse che l’elettrone percorresse solo quelle orbite circolari per le
quali il suo momento angolare l = r × mv avesse modulo dato da un multiplo intero di h/2π (poichè
l’orbita circolare è piana e la forza agente è centrale, la direzione ed il verso di l sono perfettemante
determinate). In altre parole, Bohr impose che
l = mvr = n
h
= n~
2π
(5.7)
dove n = 1, 2, 3, · · · è detto numero quantico. Bohr impose poi che l’elettrone accomodato su una tale
orbita non irraggiasse energia elettromagnetica. Per questo motivo, furono chiamate orbite stazionarie e
i corrispondenti stati furono detti stati stazionari.
Quando un elettrone si trova su un’orbita stazionaria permessa, esiste perfetto bilanciamento tra la
forza centrifuga legata alla sua rotazione e la forza di attrazione elettrostatica
mv 2
1 e2
=
r
4π0 r2
.
(5.8)
Combinando questa equazione con la regola di quantizzazione del momento angolare data dall’eq.(5.7),
si ottiene immediatamente l’espressione per il raggio delle orbite stazionarie:
r=
h2 0 2
n = a0 n2
πme2
(5.9)
a0 =
h2 0
= 0.529 Å
πme2
(5.10)
dove abbiamo posto
CAPITOLO 5. LA FISICA DEI QUANTI
25
Figura 5.5: Struttura dei livelli energetici degli stati stazionari dell’atomo di idrogeno secondo il modello
di Bohr.
detto raggio di Bohr. Questo risultato dimostra in modo naturale che, come conseguenza del primo
postulato, le orbite elettroniche sono quantizzate per quanto riguarda il loro raggio, a0 essendo il valore di
tale raggio nello stato n = 1. Questo particolare stato stazionario è chiamato stato fondamentale. Tutti
gli altri stati, cioè quelli corripondenti ad n > 1, sono chiamati stati eccitati. La condizione limite di
n → +∞ corrisponde allo stato non legato: l’atomo di idrogeno è stato ionizzato, ovvero l’elettrone ed il
protone sono stati portati a distanza infinita.
Il primo postulato determina un’altra importante regola di quantizzazione: quella sull’energia dell’atomo. Calcoliamo, infatti, l’energia totale ET elettronica come somma di un contributo cinetico Ecin ed
uno potenziale Epot :
1 e2
1
(5.11)
ET = Ecin + Epot = mv 2 −
2
4π0 r
dove il segno negativo dell’energia potenziale elettrostatica tiene conto del fatto che elettrone e nucleo
hanno carica opposta. Ricavando il valore di v dalla (2.7) ed utilizzando l’espressione quantizzata per r
otteniamo
me4 1
1
ET = − 2 2 2 = −13.6 eV 2 .
(5.12)
80 h n
n
Questo risultato è di fondamentale importanza: seguendo il modello di Bohr abbiamo dimostrato in modo
ovvio che le energie degli stati stazionari sono distribuite discretamente. In particolare, l’energia dello
stato fondamentale risulta essere pari a -13.6 eV (corrispondente al valore n = 1), in eccellente accordo
con i dati sperimentali: essa, infatti, coincide con l’energia di ionizzazione dell’atomo di idrogeno. La
struttura dei livelli energetici è rappresentata in Fig.5.5.
Il modello è completato dal secondo postulato: la radiazione elettromagnetica viene emessa o assorbita
da un atomo di idrogeno quando l’elettrone compie una transizione da uno stato stazionario ad un altro.
Inoltre, la frequenza ν della radiazione è legata alle energie elettroniche nello stato iniziale Ei e finale Ef
secondo la semplice relazione:
Ei − Ef
ν=
.
(5.13)
h
Ovviamente, risulta che:
• se Ei > Ef si ha emissione di radiazione,
• se Ei < Ef si ha assorbimento di radiazione.
Seguendo il concetto di quanto di luce introdotto da Einstein, diremo che ogni transizione elettronica tra
due stati stazionari comporta l’emissione o l’assorbimento di un fotone di energia pari alla differenza tra
le energie degli stati interessati alla transizione. Tenuto conto che tali energie sono negative (perchè
corrispondono a stati legati), allora si ha emissione di un fotone quando si passa da uno stato più
eccitato ad uno meno eccitato. Il viceversa vale per l’assorbimento di radiazione. La Fig.5.6 rappresenta
schematicamente i due casi.
CAPITOLO 5. LA FISICA DEI QUANTI
26
Figura 5.6: Transizioni tra stati stazionari che comportano emissione (a sinistra) o assorbimento (a destra)
di un fotone.
Figura 5.7: Orbite stazionarie, livelli energetici e transizioni permesse (emissione) per l’atomo di idrogeno
secondo il modello di Bohr.
CAPITOLO 5. LA FISICA DEI QUANTI
27
Se facciamo uso dell’eq.(5.120 possiamo quantificare in modo esplicito la lunghezza d’onda λ dei fotoni
emessi o assorbiti:
1
1
ν
Ei − Ef
me4
1
−
(5.14)
= =
=
λ
c
ch
80 h3 c n2f
n2i
dove ni ed nf sono i numeri quantici che definiscono, rispettivamente, lo stato stazionario iniziale e finale
coinvolti nella transizione elettronica.
Questo risultato è notevole per due ragioni: (i) esso fornisce una giustificazione formale per la legge
empirica di Rydberg; (ii) il valore della costante è
me4
= 109737 cm−1
80 h3 c
(5.15)
in ottimo accordo con il valore sperimentale della costante di Rydberg R. In altre parole, il modello di
Bohr non solo spiega qualitativamente il meccanismo di emissione/assorbimento di radiazione da parte di
un atomo, giustificando pienamente la natura discreta degli spettri atomici, ma prevede quantitativamente
in modo esatto la posizione delle righe spettrali delle diverse serie di Lyman (nf =1), Balmer (nf =2),
Paschen (nf =3), Brackett (nf =4) e Pfund (nf =5). Il quadro concettuale che abbiamo fin qui sviluppato
è graficamente riassunto in Fig.5.7.
5.3
Estensioni del modello di Bohr
Il modello di Bohr si presta a due semplici estensioni che lo rendono idoneo a spiegare gli spettri atomici
di atomi più complessi dell’idrogeno ed a migliorare l’accordo con i dati sperimentali sulla costante di
Rydberg.
Consideriamo, infatti, quella classe di atomi detti idrogenoidi. Essi sono, come l’atomo di idrogeno,
formati da un solo elettrone in orbita attorno ad un nucleo di carica atomica +Ze, con Z > 1. Con
riferimento alla tabella periodica degli elementi è facile convincersi che gli ioni He+ , Li++ , ... rientrano
in questa definizione. Per gli atomi idrogenoidi il problema dell’interazione elettrone–nucleo può essere
trattato in maniera analoga a quanto fatto nel precedente paragrafo, con l’unica accortezza di considerare
la carica nucleare +Ze. Ne segue immediatamente che le formule per i raggi delle orbite stazionarie e per
le relative energie sono dati, rispettivamente, da:
r=
a0 n2
Z
(5.16)
e
Z2
.
(5.17)
n2
All’aumentare, quindi, del numero atomico Z le orbite stazionarie risultano sempre più “strette” (a parità
di numero quantico n) e di maggior energia di legame. Ciò indica che, fissato n, più il nucleo è carico,
più fortemente è legato l’elettrone, come è ragionevole aspettarsi.
L’ipotesi fino ad ora implicitamente assunta è che la massa del nucleo (sia per l’atomo di idrogeno, che
per gli atomi idrogenoidi) fosse talmente maggiore di quella dell’elettrone, da poter essere considerata a
tutti gli effetti pratici infinita. Un’analisi più rigorosa, invece, attribuisce al nucleo una massa pari a Amp ,
dove A è il numero di massa per l’atomo considerato, mentre mp = 1.67 × 10−27 Kg rappresenta la massa
del protone. In questo caso, il moto di rivoluzione dell’elettrone non è più quello di una particella in orbita
attorno ad un centro fisso. Piuttosto, come previsto dalla meccanica classica, si deve parlare del moto di
rotazione di nucleo ed elettrone attorno al centro di massa del sistema atomico. È relativamente facile
dimostrare che in questo caso la costante di Rydberg data nelle eq.(5.14) e (5.15) deve essere riscritta
come:
1
me4
R= 2 3
(5.18)
me
80 h c 1 + Am
p
ET = −13.6eV
dove, per maggior chiarezza, abbiamo chiamato con me la massa dell’elettrone. Se consideriamo l’atomo
di idrogeno (cioè A = 1), allora otteniamo per la costante di Rydberg il valore di 109678 cm−1 in
praticamente perfetto accordo col dato sperimentale di eq.(5.1).
CAPITOLO 5. LA FISICA DEI QUANTI
28
Figura 5.8: Schema dell’apparato sperimentale di Davisson e Germer per la diffrazione di un fascio di
elettroni da parte di un cristallo.
5.4
L’ipotesi di de Broglie ed il dualismo onda–corpuscolo
Terminiamo sul concetto di dualismo onda–corpuscolo già anticipato a proposito dell’effetto fotoelettrico.
L’introduzione dell’ipotesi di fotone permise ad Einstein di spiegare mirabilmente le risultanze sperimentali ed introdusse un importante concetto: la radiazione elettromagnetica può essere equivalentemente
descritta in termini ondulatori (elettromagnetismo classico) od in termini corpuscolari (fotoni) a seconda
della specifica fenomenologia che si consideri. Tutto il capitolo della spettroscopia atomica è, per esempio,
sotteso dal concetto di fotone che diventa la particella scambiata durante l’interazione tra la radiazione
e la materia.
Questa idea di dualità è davvero molto suggestiva ed efficace e fu ripresa da L. de Broglie nel 1924
che la estese anche alle particelle materiali. L’idea di base fu semplice: se la luce può manifestarsi come
onda (in accordo alla nostra esperienza quotidiana) o come corpuscolo (come in fisica atomica), perchè
questa cosa non potrebbe essere vera anche per una particella? In altre parole, possiamo ammettere che
ad una particella di quantità di moto p ed energia E sia possibile associare una lunghezza d’onda di de
Broglie λ data dalla
h
(5.19)
λ=
p
cui corrisponde una frequenza
E
.
(5.20)
h
Un modo alternativo di esprime queste due relazioni è quello che fa uso del vettor d’onda k = 2π/λ e
della frequenza angolare (o pulsazione) ω = 2πν:
ν=
p = ~k
E = ~ω
.
(5.21)
In questo contesto spesso si parla di onde di materia associate ad una certa particella.
L’ipotesi di de Broglie fu confermata da un esperimento condotto da Davisson e Germer secondo lo
schema illustrato in Fig.5.8.
Un fascio di particelle (elettroni) viene emesso da un’opportuna sorgente e collimato su un bersaglio
costituito da un pezzo di cristallo. Il fascio diffratto viene, invece, raccolto da un rivelatore posto simmetricamente alla sorgente. Le risultanze sperimentali dimostrarono che il fascio diffratto presentava una
serie di massimi di intensità quando fosse verificata la seguente relazione tra la lunghezza d’onda di de
Broglie λ degli elettroni e la separazione d tra i diversi piani reticolari del cristallo:
2dsinθ = nλ
(5.22)
dove θ è l’angolo formato dal fascio di elettroni e la superficie del cristallo, mentre n è un numero intero.
La spiegazione di questo esperimento risulta semplice se si considera cosa avviene a livello microscopico
quando il fascio di elettroni interagisce col cristallo. La situazione, illustrata in Fig. 5.9, corrisponde
ad un fascio di particelle che, riflesse dai diversi piani reticolari, finiscono col creare un fenomeno di
CAPITOLO 5. LA FISICA DEI QUANTI
29
Figura 5.9: Spiegazione della condizione di interferenza costruttiva per il fascio di elettroni diffratto
(condizione di Bragg).
interferenza sul rivelatore. Come noto dall’ottica geometrica, quando due fasci luminosi emessi da due
sorgenti coerenti (cioè a differenza di fase costante e stessa lunghezza d’onda) compiono, per arrivare
ad un rivelatore, dei cammini ottici che differiscono per un numero intero di lunghezze d’onda, allora
si manifesta il fenomeno di interferenza costruttiva. Sul rivelatore, cioè, si osservano dei massimi di
diffrazione4 . Analizzando il cammino ottico persorso dai diversi fasci di elettroni (si veda la Fig.5.9)
si deduce immediatamente che la condizione di massimo fascio diffratto osservata nell’esperimento di
Davisson e Germer corrisponde proprio a quella di interferenza costruttiva nota in ottica (condizione
di Bragg). In altre parole, l’esperimento in questione dimostra che un fascio di particelle (elettroni)
si comporta esattamente come un’onda luminosa, di lunghezza λ data dalla relazione di de Broglie.
Questo esperimento, quindi, è la migliore dimostrazione pratica che l’ipotesi ondulatoria espressa anche
a proposito di particelle materiali è vera.
In conclusione, sommando l’ipotesi di Einstein sui fotoni (dimostrata dall’effetto fotoelettrico) e quella
di de Broglie sulle onde materiali (dimostrata dalla diffrazione di elettroni) possiamo enunciare compiutamente il concetto di dualismo onda–corpuscolo: ogni fenomeno naturale si manifesta, a seconda dei
casi, o in modo ondulatorio, o in modo corpuscolare. Nel mondo macroscopico (quello legato alla nostra
esperienza quotidiana) le particelle massive sono ben descritte da corpuscoli che seguono la meccanica
classica, mentre i fenomeni di propagazione del campo elettromagnetico sono efficacemente descritti dalle
leggi dell’ottica (geometrica o fisica). Al contrario, spesso il mondo microscopico (che sfugge alla nostra
diretta esperienza sensoriale) si manifesta in modo opposto: la radiazione elettromagnetica è efficacemente descritta come fascio di corpuscoli o fotoni, mentre le particelle obbediscono alle leggi tipiche delle
onde (come, ad esempio, la diffrazione).
5.5
Il principio di indeterminazione di Heisenberg
Una volta introdotto il concetto di dualismo onda-corpuscolo e quello di onda di materia, possiamo
chiederci che tipo di onda rappresenti matematicamente una certa particella. La risposta è semplice e
immediata nel caso di una particella libera: in questo caso l’onda materiale a essa associata sarà un’onda
piana di tipo armonico5 che, in una dimensione, è rappresentata nella Fig.5.10 (destra).
Un’onda piana ha ampiezza costante. Essa correttamente descrive un’onda di materia (associata a
una particella libera) che deve essere simile in tutti i punti dello spazio. Ciò è consistente col fatto che,
essendo la particella libera, non esiste un potenziale di interazione il quale, agendo sulla particella, possa
distorcerne l’onda associata.
4 La discussione del fenomeno di interferenza costruttiva tra onde luminose è descritto nel libro di R. Mazzoldi, M. Nigro
e C. Voci, “Fisica II - Elettromagnetismo ed onde” (casa editrice EdiSES).
5 Ricordiamo che un’onda si dice piana quando il suo fronte d’onda - cioè il luogo geometrico dei punti nello spazio che
vengono investiti allo stesso istante dall’onda che avanza - è rappresentato da un piano. Il carattere armonico di un’onda,
invece, è legato alla legge matematica che esprime la variazione dell’ampiezza dell’onda nel tempo: quando tale legge è
espressa da una funzione trigonometrica seno o coseno, allora l’onda è armonica.
CAPITOLO 5. LA FISICA DEI QUANTI
30
Figura 5.10: Rappresentazione uno-dimensionale dell’onda materiale associata a una particella libera
(destra) e a una particella confinata nella regione di spazio ∆x (sinistra).
Più complesso, ma molto più interessante, è il caso di una particella confinata in una regione di spazio.
Tratteremo il caso uno–dimensionale in cui la regione di confinamento ha spessore ∆x. Questo modello
rappresenta il caso di una particella confinata in una buca di potenziale. L’onda di materia che descrive
una tale sitazione non potrà avere in questo caso ampiezza costante: è ovvio, infatti, che nella regione ∆x
l’intensità dell’onda (che, ricordiamolo, è legata al quadrato della sua ampiezza) sarà massima perchè ivi
è localizzata la particella. Al contrario, fuori da tale regione l’onda dovrà avere ampiezza molto minore e,
nel limite di grande distanza dalla regione ∆x o di profondità infinita della buca di potenziale, risulterà
rispettivamente trascurabilmente piccola o rigorosamente nulla. Una buona rappresentazione matematica
di questa onda è data nella Fig.5.10 a sinistra. Questo profilo di onda materiale è chiamato pacchetto
d’onda di ampiezza ∆x.
Il numero di lunghezze d’onda λ del pacchetto sarà ovviamente legato allo spessore ∆x della zona di
confinamento della particella e, quindi, potremo scrivere
∆x ∼ nλ λ
(5.23)
dove nλ è il numero di lunghezze d’onda contenute in ∆x. Ricordando la relazione esistente tra la
lunghezza d’onda λ e il numero d’onda k possiamo riformulare la precedente relazione come
∆x∆k ∼ 2π
(5.24)
dove abbiamo introdotto anche un intervallo finito ∆k per il numero d’onda in accordo all’analisi di
Fourier6 . La relazione di de Broglie consente di riscrivere questo risultato nella forma
∆x∆p ∼ h
(5.25)
In generale, tuttavia, noi conosciamo la regione di localizzazione di un’onda materiale con ancor minore
accuratezza di quanto assunto in questo ragionamento. Conseguentemente la precedente equazione non
può rappresentare altro che un limite superiore di precisione nella determinazione delle incertezze ∆x e
∆p sulla posizione e sulla quantità di moto della particella. In generale, quindi, dovremo ammettere che
∆x∆p ≥ h
(5.26)
Questo risultato di importanza fondamentale è noto come principio di indeterminazione di Heisenberg.
Le sue conseguenze concettuali sono molto profonde e scavano un ulteriore solco tra i concetti della fisica
6 In altre parole, secondo l’analisi di Fourier noi possiamo rappresentare il pacchetto d’onda di figura 2.10 (sinistra) tramite
un’opportuna sovrapposizione di onde sinusoidali semplici (cioè di onde armoniche). Un pacchetto d’onda di ampiezza ∆x
richiede la sovrapposione di tutte quelle onde armoniche il cui numero d’onda cada nell’intervallo ∆k definito dall’equazione
(2.27).
CAPITOLO 5. LA FISICA DEI QUANTI
31
Figura 5.11: Rappresentazione schematica di una riga spettrale di assorbimento in alta risoluzione.
classica e quelli della fisica quantistica: a livello microscopico, infatti, risulta impossibile determinare
contemporaneamente con precisione assoluta (cioè con incertezza nulla) la posizione e la quantità di moto
di una particella. Questo risultato, che discende direttamente dal dualismo onda-corpuscolo, impedisce
quindi che una certa misura sperimentale determini con assoluta accuratezza contemporaneamente la
posizione e la velocità di un corpuscolo. Al più, infatti, potremmo misurare l’una e l’altra con un certo
margine di errore per ciascuna grandezza, essendo gli errori di misura legati dalla relazione di cui sopra.
Alternativamente, potremmo determinare precisamente l’una (incertezza nulla) senza tuttavia poter fare
previsione alcuna sull’altra (incertezza infinita).
È importante sottolineare che il principio di indeterminazione non è legato alla precisione degli strumenti di misura. In altre parole, esso non è dovuto al fatto che ogni misura sperimentale è in varia
maniera afflitta da errore. Al contrario, l’indeterminazione che lega posizione e quantità di moto è la
manifestazione di proprietà fondamentali della materia legate alla sua duale natura onda-corpuscolo.
Il principio di indeterminazione ha numerose evidenze sperimentali, alcune delle quali molto spettacolari. Consideriamo, infatti, un sistema costituito da atomi di elio. È stato sperimentalmente dimostrato
che, anche raffreddando questo sistema a una temperatura assoluta praticamente nulla, esso non solidifica. Se, infatti, il sistema solidificasse a T = 0 K noi potremmo conoscere con assoluta certezza e
contemporaneamente la velocità di ciascun atomo di elio (che risulterebbe nulla) e la sua posizione nel
sistema solidificato. Ciò violerebbe il principio di indeterminazione. È necessario, quindi, che anche a T
= 0 K gli atomi siano animati da un flebile moto di vibrazione (detto moto di punto zero) che non ha
analogo classico in teoria cinetica dei gas, ma che assicura quella indispensabile incertezza su posizione
e velocità tale da rispettare l’equazione (2.29). Questo flebile moto di agitazione è sufficiente, nel caso
dell’elio, a impedire la solidificazione. In altre parole, la temperatura cinetica associata a esso è superiore
alla temperatura di fusione dell’elio.
Il principio di indeterminazione di Heisenberg può essere esteso anche ad un’altra coppia di grandezze
fisiche: l’energia E e il tempo t. In particolare, si può dimostrare che
∆E∆t ≥ h
(5.27)
estendendo anche a questa coppia tutte le considerazioni sviluppate per posizione e quantità di moto.
Anche questa seconda versione del principio ha una convincente verifica sperimentale legata alla spettro di
assorbimento di un atomo. Noi associamo l’assorbimento di un fotone da parte di un atomo alla transizione
tra due stati stazionari di energia, rispettivamente, E1 (stato iniziale) e E2 (stato eccitato finale). Una
misura spettroscopica segnala l’avvenuta transizione tramite una riga nello spettro di assorbimento alla
frequenza ν definita dalla relazione ν = (E2 − E1 )/h. Quando la misura è condotta in condizioni di
altissima risoluzione si osserva che la riga spettrale ha una struttura: in particolare, essa ha la forma
rappresentata schematicamente nella figura 2.11 (destra).
CAPITOLO 5. LA FISICA DEI QUANTI
32
La larghezza finita della riga corrisponde a un certo intervallo di frequenze ∆ν il cui inverso ∆t è
interpretato come il tempo di vita medio dello stato eccitato. Se questo tempo di vita è finito, allora
ci deve essere una corrispondente incertezza ∆E2 sull’energia dello stato eccitato raggiunto durante la
transizione. Lo schema di Bohr per i livelli energetici degli stati stazionari è conseguentemente modificato
come illustrato a sinistra nella Fig.5.11. Misure a alta risoluzione hanno effettivamente confermato questa
interpretazione, fornendo una stima del tempo di vita di uno stato eccitato e del corrispondente intervallo
di energie associate a uno stato stazionario perfettamente in accordo con il principio di indeterminazione
di Heisenberg.
5.6
Momenti magnetici associati ai moti orbitali elettronici
Consideriamo, nell’ambito del modello atomico di Bohr, il moto di rivoluzione di un elettrone attorno al
nucleo sull’orbita stazionaria di raggio r. Poichè l’elettrone porta una carica −e, possiamo idealmente
associare a tale moto una corrente i = −eω/2π, dove abbiamo introdotto la velocità angolare di rotazione
ω. Come noto dalla teoria classica dell’elettromagnetismo, possiamo associare a questa corrente (che
idealmente fluisce lungo un’orbita elettronica di raggio r) un momento di dipolo magnetico7 definito
come segue:
1
ω
(5.28)
ML = −e πr2 = − eωr2 .
2π
2
Ricordando che classicamente il momento angolare vale in modulo L = mωr2 , possiamo riscrivere
l’eq.(5.28) in forma vettoriale:
e
L .
(5.29)
ML = −
2m
Questa relazione è valida sia nella fisica dei quanti (purchè si utilizzi l’opportuna espressione quantizzata
del momento angolare), sia in meccanica quantistica (dove viene fornita la giustificazione più rigorosa e
formale di questa relazione).
Il concetto chiave è che ad ogni momento angolare orbitale elettronico è associato un momento magnetico. È proprio tramite tale momento magnetico che un atomo interagisce con un eventuale campo
magnetico su di esso acceso.
5.7
Lo spin
Supponiamo ora di considerare un atomo “preparato” in uno stato tale per cui il momento angolare
L dell’elettrone sia nullo. In queste condizioni l’azione di un campo magnetico esterno sull’atomo è
ovviamente nulla.
Nel 1924 Stern e Gerlach condussero un esperimento esattamente in queste condizioni: l’idea era
proprio quella di verificare quanto detto. Essi misero a punto un apparato schematicamente descritto in
Fig.5.12: un fascio di atomi con L = 0 veniva emesso da una sorgente S e fatto passare attraverso i poli
di un magnete M che generava un campo magnetico costante, ma non uniforme. Il fascio veniva poi
raccolto da un opportuno rivelatore R. L’aspettativa di Stern e Gerlach era quella di osservare su R una
sola impronta: il fascio non avrebbe dovuto essere deflesso, in base alle considerazioni fatte. Al contrario,
le evidenze sperimentali dimostrarono che il fascio veniva separato in due componenti che risultavano
deflesse in modo simmetrico rispetto alla direzione del fascio incidente.
Questo risultato è sorprendente. Se ragioniamo in termini classici, avremmo dovuto aspettarci una
traccia continua (e non solo due impronte), corrispondente a tutte le possibili orientazioni che classicamente un momento magnetico ML può assumere rispetto alla direzione del campo. Al contrario,
ragionando in termini fisica dei quanti, avremmo dovuto aspettarci una sola impronta, perchè per L=0
non c’è interazione (e, dunque, deflessione) tra fascio atomico e campo magnetico. Insomma: l’esistenza
di due traccie simmetriche non può essere spiegata nè classicamente, nè con la teoria dei quanti fin qui
sviluppata.
L’enigma fu risolto da Goudsmit e Uhlenbeck nel 1926: essi, infatti, ipotizzarono che l’elettrone
possedesse un nuovo grado di libertà cui fosse associato un diverso momento magnetico, non nullo anche
7 Possiamo,
infatti, applicare il principio di equivalenza di Ampere.
CAPITOLO 5. LA FISICA DEI QUANTI
33
Figura 5.12: Schema dell’apparato sperimentale di Stern e Gerlach.
per gli stati ad L = 0. Questo nuovo grado di libertà non ha analogo classico e venne chiamato spin8 .
Ad esso, in analogia a quanto fatto per il momento magnetico orbitale ML , viene associato un momento
magnetico di spin
e
S
(5.30)
MS = −g
2m
dove g è una costante chiamata rapporto giromagnetico dell’elettrone il cui valore è circa 2.
Fu, inoltre, postulato che il nuovo momento angolare di spin S avesse una caratteristica speciale,
ovvero che la sua componente Sz lungo una direzione arbitraria potesse assumere sempre e solo due
valori possibili
Sz =
1
~ stati con spin “up00
2
1
Sz = − ~ stati con spin “down00
2
.
(5.31)
In questo modo, si riesce a fornire una giustificazione (euristica) dell’esperimento di Stern-Gerlach: il
fascio di atomi non interagisce col campo magnetico tramite i momenti magnetici orbitali (che sono nulli
perchè è stato preparato in modo che L=0), bensı̀ tramite il momento magnetico di spin che può assumere
solo i due valori
e 1
MSz = ±g
~ .
(5.32)
2m 2
L’importanza di questo risultato è fondamentale: l’elettrone dovrà d’ora in poi essere descritto da
quattro gradi di libertà: tre spaziali ed uno di spin.
8 Per semplificare le cose, si può immaginare che questo grado di libertà sia associato al moto di rotazione dell’elettone
attorno al proprio asse. Poichè l’elettrone è carico, anche questa rotazione assiale comporta l’esistenza di una corrente e,
quindi, di un momento magnetico di spin. E’, tuttavia, doveroso osservare che questa immagine, anche se efficace, non
è rigorosamente vera. In realtà, infatti, lo spin elettronico è un effetto relativistico: solo una trattazione quantistico–
relativistica, infatti, consente in modo naturale di introdurre e giustificare pienamente questo nuovo grado di libertà.