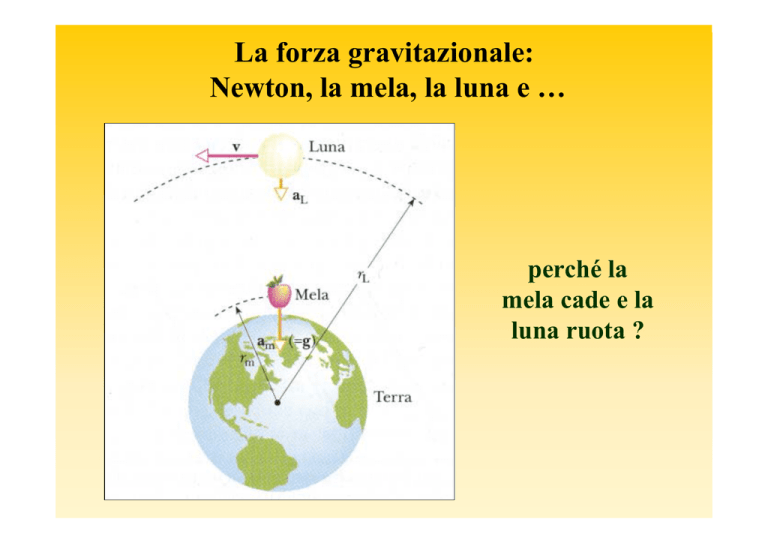
La forza gravitazionale:
Newton, la mela, la luna e …
perché la
mela cade e la
luna ruota ?
• La causa dei due fenomeni è la stessa
• Accelerazione luna : aL = 0.0027 m/s2
• Accelerazione mela : am = 9.81 m/s2 = g
• Entrambe le acc. sono dirette verso il centro della Terra
come si calcolano?
La forza gravitazionale:
G
m1 ⋅ m 2 G
F=-G
⋅ ur
2
r
F21 : forza sulla massa 2
dovuta alla massa 1
G = 6.674⋅10-11 m3/(kg⋅s2)
F12 : forza sulla massa 1
dovuta alla massa 2
Il sistema Terra-luna
(foto eseguita dal
veicolo spaziale Galileo,
a 6.2 106 km)
G
m1 ⋅ m 2 G
F=-G
⋅ ur
2
r
Orbite di proiettili
lanciati
orizzontalmente in
prossimità della
sup. terrestre, con
diverse velocità
iniziali
La forza elettrostatica:
attrazione e repulsione
La legge di Coulomb per la forza
elettrostatica
G
q1 ⋅ q 2 G
F = K 2 ⋅ ur
r
K=
1
≈ 9 ⋅109 N ⋅ m2 / C2
4 ⋅ π ⋅ ε0
ε0 = 8.854⋅10-12 C2 / (N⋅ m2 )
Forze centrali
• La forza di gravità e la forza di Coulomb sono
esempi di forze centrali.
• Elemento caratterizzante di una forza centrale: le
rette d’azione delle forze passano per le sorgenti
dell’interazione.
• Analogie e differenze fra forza gravitazionale e
forza elettrostatica
perché alcune proprietà sono analoghe ed altre no ?
Il lavoro della forza
peso
dipende solo dalla
differenza di quota
Il lavoro di una forza centrale non dipende dal percorso
Le forze centrali sono conservative
Per le forze conservative è possibile
definire una energia potenziale
Lavoro = - ∆ Epotenziale
Energia potenziale
gravitazionale:
Epot = mgh
z è misurata rispetto ad una
posizione z=0
soltanto∆ Epotenziale è misurabile
Forza gravitazionale e forza elettrostatica:
interazione tra 2 masse o tra 2 cariche
Per spiegarle:
Azione “a distanza”
Interazione attraverso il “campo”
Massa 1
CAMPO
Massa 2
Carica 1
CAMPO
Carica 2
Verso il concetto di campo:
il vettore g
Verso il concetto di campo:
il vettore g
G
m1 ⋅ m2 G
F =-G
⋅ ur
2
r
mT G
G
g = - G 2 ⋅ ur
RT
G
G
P = mg
P = mg
G
G
F
g=
mrif
Verso il concetto di campo
(scalare e vettoriale):
una grandezza fisica (scalare o vettoriale), alla quale,
per ogni punto di una determinata regione di spazio, si
può assegnare un valore definito
Esempio:
Valori di pressione e
temperatura, rilevati
sulla regione della
Gran Bretagna, in un
giorno di dicembre
2003
Temperature (°C)
Pressioni (bar)
Due esempi di campi scalari:
Curve isoterme e curve isobare
sulla Gran Bretagna, in un giorno di dicembre 2003
Linee di egual
temperatura (°C)
Linee di egual
pressione (bar)
Un esempio di campo vettoriale:
La velocità del vento, sulla Gran Bretagna,
in un giorno di dicembre 2003
Il campo : un “condizionamento” dello spazio,
rilevabile tramite “sonda” di prova opportuna
G
G
F
H=
" sonda"
“sonda”: massa (puntiforme e non)
carica elettrica (puntiforme e non)
Come si rappresenta un campo?
• Le linee di forza
• Le equazioni del campo
Campo
gravitazionale:
la forza agente su
una “massa di
prova”
Campo
elettrostatico della
carica +q:
la forza agente su
una “carica di
prova”
Linee di forza per il campo di una carica puntiforme
Linee di forza per il campo gravitazionale terrestre
Linee di forza e
superfici ad energia
potenziale costante
per una carica
positiva puntiforme.
Quale grafico si
otterrebbe per una
massa puntiforme?
PRINCIPIO DI
SOVRAPPOSIZIONE
DEGLI EFFETTI:
G
G
G
Eris = ETerra + ELuna
Il campo gravitazionale
generato
dalla Terra e dalla Luna
PRINCIPIO DI
SOVRAPPOSIZIONE
DEGLI EFFETTI:
G
G G
Eris = E1 + E2
Il campo elettrostatico
generato
da due cariche uguali e
positive
PRINCIPIO DI SOVRAPPOSIZIONE DEGLI EFFETTI
q2
Nel punto P:
E=E1+E2+E3
q1
q3
Esistono veramente oggetti “puntiformi” ?
Per masse non puntiformi (distribuite), come mi comporto ?
• In generale, si sfrutta il principio di sovrapposizione
degli effetti.
• In casi particolari (simmetria nella distribuzione
delle sorgenti dell’interazione) si possono avere
semplificazioni ulteriori
ESERCIZIO
Date due cariche Q1 (= - 1⋅ 10-8 C) e Q2 (= +3⋅10-8 C), poste
ad una distanza d, determinare in quali punti lungo la retta
congiungente il campo elettrostatico da esse creato è nullo.
d
Q2 =
I
Q1= + 3⋅10-8
-1⋅10-8
II
III
ESERCIZIO
P1
Quanto
vale il
campo
elettrico in
P1 e in P2?
Q1= +1⋅10-8
P2
Q2= -1⋅10-8
Q3= +1⋅10-8












