Resistenza elettrica

Resistenza elettrica
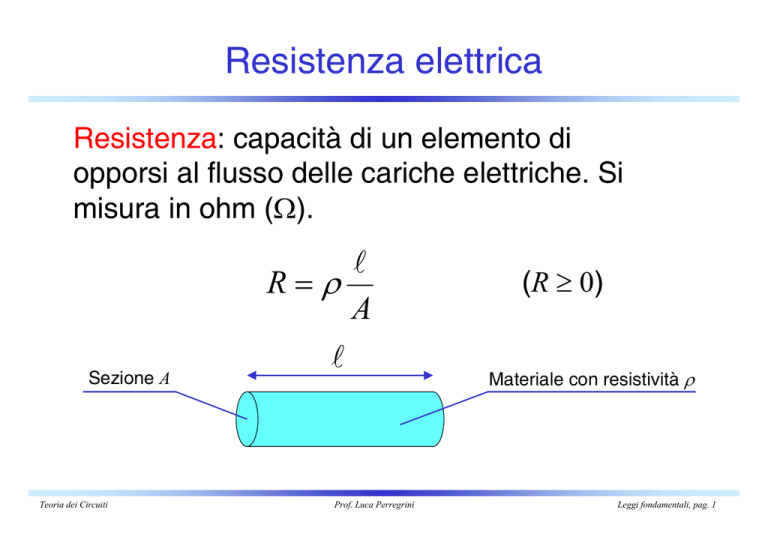
Resistenza: capacità di un elemento di
opporsi al flusso delle cariche elettriche. Si
misura in ohm (Ω).
Sezione A
Teoria dei Circuiti
l
R=ρ
A
l
Prof. Luca Perregrini
(R ≥ 0)
Materiale con resistività ρ
Leggi fondamentali, pag. 1
Legge di Ohm
La tensione v su un resistore è direttamente
proporzionale alla corrente i che lo attraversa.
La costante di proporzionalità è la resistenza R.
i
R
Teoria dei Circuiti
v = R ⋅i
+
v
(con la convenzione
degli utilizzatori)
–
1 Ω = 1 V/A
Prof. Luca Perregrini
Leggi fondamentali, pag. 2
Corto circuito
i
i
R=0
+
v
+
v=0
–
–
v = R ⋅i = 0
La tensione v è nulla qualunque sia la corrente i
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 3
Circuito aperto
i=0
i
R=∞
+
v
+
v
–
–
v
i = lim = 0
R →∞ R
La corrente i è nulla qualunque sia la tensione v
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 4
Conduttanza
Conduttanza: capacità di un elemento di
condurre la corrente elettrica. Si misura in
siemens (S)
1 i
G= =
R v
(G ≥ 0)
1 S = 1 Ω–1 = 1 A/V
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 5
Potenza dissipata da un resistore
2
i
p = v ⋅ i = (R ⋅ i ) ⋅ i = R ⋅ i =
G
2
2
v v
2
p = v ⋅i = v ⋅ =
= G ⋅v
R R
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 6
Potenza dissipata da un resistore
2
2
i
v
2
p = v ⋅i = R ⋅i =
= v ⋅G =
G
R
2
La potenza è funzione non lineare della corrente
o della tensione.
Ricordando che R ≥ 0 e G ≥ 0 si ha che p ≥ 0 e
quindi un resistore assorbe sempre potenza dal
circuito (elemento passivo).
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 7
Rami, nodi e maglie
Ramo: singolo elemento a due terminali (bipolo)
incluso nel circuito.
R1
v
Teoria dei Circuiti
+
–
R2
R3
Prof. Luca Perregrini
i
Leggi fondamentali, pag. 8
Rami, nodi e maglie
Nodo: punto di interconnessione di due o più
rami.
a
v
+
–
R1
b
R2
R3
i
c
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 9
Rami, nodi e maglie
Maglia: percorso chiuso ottenuto passando non
più di una volta attraverso una qualunque
sequenza di nodi.
R1
v
Teoria dei Circuiti
+
–
R2
R3
Prof. Luca Perregrini
i
Leggi fondamentali, pag. 10
Rami, nodi e maglie
Maglia indipendente: maglia che contiene un
ramo che non appartiene a nessun’altra maglia.
Nrami = Nmaglie indipendenti + Nnodi – 1
Maglie indipendenti danno luogo ad equazioni
indipendenti
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 11
Elementi in serie e in parallelo
Due o più elementi sono detti in serie se sono
concatenati (percorsi dalla stessa corrente)
i
Teoria dei Circuiti
i
Prof. Luca Perregrini
i
Leggi fondamentali, pag. 12
Elementi in serie e in parallelo
Due o più elementi sono detti in parallelo se
sono collegati alla stessa coppia di nodi
(stessa tensione ai capi)
+
v
–
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 13
Legge di Kirchhoff delle correnti (KCL)
La somma algebrica delle correnti che entrano
in un nodo è zero
i2
i1
i3
N
∑i
n =1
n
=0
iN
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 14
Legge di Kirchhoff delle correnti (KCL)
La somma delle correnti che entrano in un
nodo è uguale alla somma delle correnti che
escono dal nodo
Esempio:
i2
i1
i3
i5
Teoria dei Circuiti
i4
Prof. Luca Perregrini
i2 + i3 + i5 = i1 + i4
Leggi fondamentali, pag. 15
Legge di Kirchhoff delle correnti (KCL)
Generalizzazione: la somma algebrica delle
correnti che entrano in una superficie chiusa è
zero
i2
i1
i3
N
∑i
n =1
iN
Teoria dei Circuiti
n
=0
i4
Prof. Luca Perregrini
Leggi fondamentali, pag. 16
Generatori di corrente in parallelo
iT
iT
a
i1
i2
i3
a
iS
b
b
iS = i1 – i2 + i3
Il generatore di destra è equivalente al circuito
di sinistra (hanno la stessa relazione i–v ai
terminali ab).
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 17
Legge di Kirchhoff delle tensioni (KVL)
La somma algebrica delle tensioni lungo un
percorso chiuso (maglia) è zero
– v3 + –
v4 +
+
v2
M
∑v
m =1
–
+ v1 –
Teoria dei Circuiti
m
=0
+ vM –
Prof. Luca Perregrini
Leggi fondamentali, pag. 18
Legge di Kirchhoff delle tensioni (KVL)
La somma delle cadute di tensione è uguale
alla somma degli aumenti di tensione
Esempio:
+ v2 – + v3 –
v1
–
+
+
–
–
Teoria dei Circuiti
v4
v2 + v3 + v5 = v1 + v4
v5 +
Prof. Luca Perregrini
Leggi fondamentali, pag. 19
Generatori di tensione in serie
a
v1
v2
+
–
–
+
+
a
+
–
vS
+
vab
–
b
vab
vS = v1 – v2 + v3
v3
+
–
–
b
Teoria dei Circuiti
Il generatore di destra è equivalente
al circuito di sinistra (hanno la stessa
relazione i–v ai terminali ab).
Prof. Luca Perregrini
Leggi fondamentali, pag. 20
Resistori in serie
i
v
a
R1
R2
+ v – + v –
1
2
+
–
KVL:
– v + v1 + v2 = 0
Legge di Ohm:
v1 = R1· i
v2 = R2· i
b
v = (R1 + R2)· i = Req· i
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 21
Resistori in serie
i
v
a
R1
R2
+ v – + v –
1
2
+
–
b
i
v
a
Req
+ v
+
–
–
b
Req = R1 + R2
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 22
Partitore di tensione
i
v
a
Req = R1 + R2
R1
R2
+ v – + v –
1
2
+
–
v
v
i=
=
Req R1 + R2
b
R1
v1 = R1 ⋅ i =
v
R1 + R2
Teoria dei Circuiti
R2
v2 = R2 ⋅ i =
v
R1 + R2
Prof. Luca Perregrini
Leggi fondamentali, pag. 23
Resistori in serie: generalizzazione
i
v
a
+
–
R1
RN
+ v –
1
+ v –
N
b
v
a
Req
+ v
+
–
–
b
N
Req = R1 + R2 + K + RN = ∑ Rn
n =1
Teoria dei Circuiti
i
Prof. Luca Perregrini
Rn
vn =
v
R1 + R2 + K + RN
Leggi fondamentali, pag. 24
Resistori in parallelo
i
v
KCL:
a
i2
i1
+
–
i = i1 + i2
R1
R2
Legge di Ohm:
i1 = v/R1
i2 = v/R2
b
v
v
v
v
i= +
=
=
R1 ⋅ R2
R1 R2
Req
R1 + R2
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 25
Resistori in parallelo
i
v
a
i
i2
i1
+
–
R1
R2
b
v
a
i
+
–
Req
b
R1 ⋅ R2
Req =
R1 + R2
Teoria dei Circuiti
Prof. Luca Perregrini
Leggi fondamentali, pag. 26
Resistori in parallelo
i
v
a
i
i2
i1
+
–
G1
G2
b
i
+
–
Geq
b
i = G1 ⋅ v + G2 ⋅ v = Geq ⋅ v
Teoria dei Circuiti
v
a
Prof. Luca Perregrini
Geq = G1 + G2
Leggi fondamentali, pag. 27
Partitore di corrente
i
v
a
i2
i1
+
–
R1 ⋅ R2
i
v = Req ⋅ i =
R1 + R2
Req = 1/Geq
R1
R2
i
i
v=
=
Geq G1 + G2
b
G1
R2
i1 =
i=
i
R1 + R2
G1 + G2
Teoria dei Circuiti
G2
R1
i2 =
i=
i
R1 + R2
G1 + G2
Prof. Luca Perregrini
Leggi fondamentali, pag. 28
Resistori in parallelo: generalizzazione
i
v
a
i
iN
i1
+
–
G1
GN
b
i
+
–
Geq
b
N
Geq = G1 + G2 + K + GN = ∑ Gn
n =1
Teoria dei Circuiti
v
a
Prof. Luca Perregrini
Gn
in =
i
G1 + G2 + K + GN
Leggi fondamentali, pag. 29
Configurazioni a stella e a triangolo
R1
Configurazione a stella
R2
v
R4
+
–
R5
Teoria dei Circuiti
R3
R6
Prof. Luca Perregrini
Configurazione a triangolo
Leggi fondamentali, pag. 30
Trasformazione stella/triangolo
3
1
Rc
Rb
3
1
R1
R2
Ra
2
R3
4
2
4
triangolo ⇒ stella
R1 =
Ra =
Rb ⋅ Rc
Ra + Rb + Rc
R1 ⋅ R2 + R2 ⋅ R3 + R3 ⋅ R1
R1
Teoria dei Circuiti
R2 =
Rc ⋅ Ra
Ra + Rb + Rc
stella ⇒ triangolo
R ⋅ R + R2 ⋅ R3 + R3 ⋅ R1
Rb = 1 2
R2
Prof. Luca Perregrini
R3 =
Rc =
Ra ⋅ Rb
Ra + Rb + Rc
R1 ⋅ R2 + R2 ⋅ R3 + R3 ⋅ R1
R3
Leggi fondamentali, pag. 31