Impianti a vapore
III.1) Studio del ciclo limite di un impianto a vapore.
Per il nostro studio andremo a considerare le macchine ideali1, si tratta cioè delle migliori macchine
che al limite si possono realizzare, mentre il fluido che evolve nel circuito lo consideriamo reale; le
trasformazioni seguite dal fluido, che negli impianti a vapore è l’acqua, sono allora reversibili. In
queste condizioni noi studiamo quello che abbiamo chiamato, nel secondo capitolo, ciclo limite.
Possiamo rappresentare il ciclo limite nei piani (T,s), (h,s) e (p,v); ognuna di queste
rappresentazioni fornisce delle diverse informazioni utili.
T
3
2
2'
1'
4
1
s
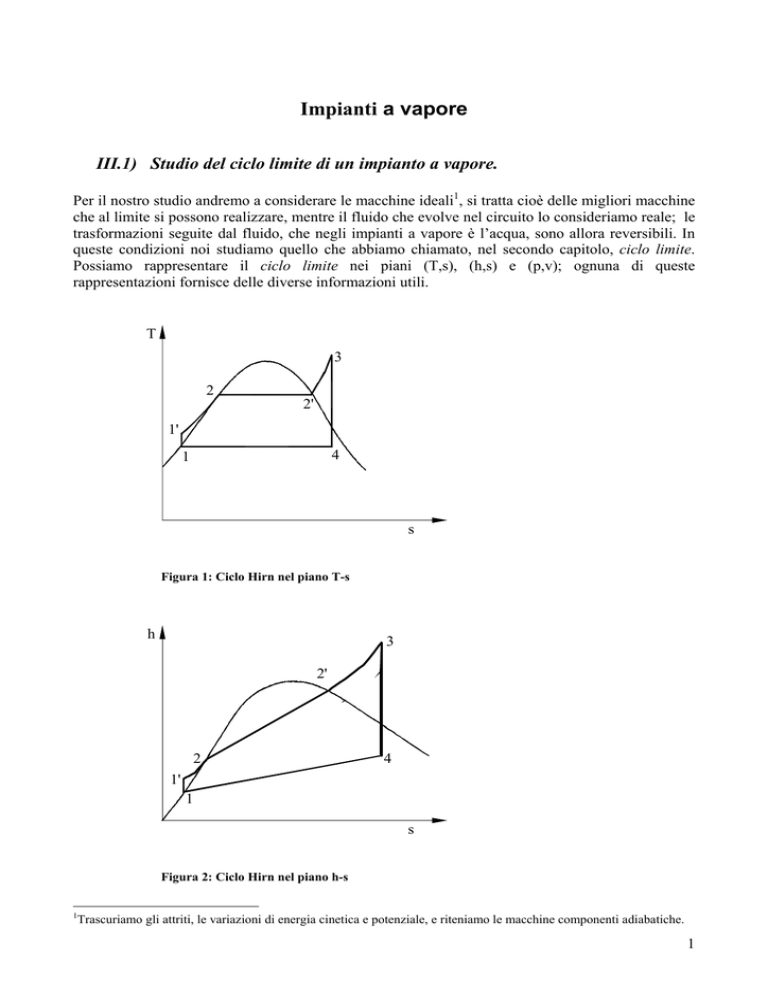
Figura 1: Ciclo Hirn nel piano T-s
h
3
2'
2
4
1'
1
s
Figura 2: Ciclo Hirn nel piano h-s
1
Trascuriamo gli attriti, le variazioni di energia cinetica e potenziale, e riteniamo le macchine componenti adiabatiche.
1
p
1'
3
2'
2
1
4
v
Figura 3: Ciclo Hirn nel piano p-v
In particolare dalla rappresentazione del ciclo nel piano (T,s) possiamo individuare immediatamente
il calore fornito al fluido, dato dall’area sottesa dalla curva 1’-3, e quello ceduto dal fluido ,dato
dall’area sottesa dalla curva 4-1; nel piano (h,s), invece, (è importante notare che le due rette 1-4 e
2-2’ hanno pendenza diversa perché sono diverse le temperature) individuiamo il lavoro di
compressione, rappresentato dalla retta 1-1’, e quello di espansione, rappresentato dalla retta 3-4;
infine nel piano (p,v) vediamo ancora il lavoro di compressione e di espansione, questa volta però
come area sottesa dalla curva, ed inoltre osserviamo le variazioni di volume specifico subite dal
fluido nelle varie trasformazioni.
Vediamo ora uno schema generale di un impianto a vapore, mettendo in evidenza i vari componenti
dell’impianto e la trasformazione che in essi viene realizzata.
Lesp
3
Q1
2'
GV
2
TV
1'
4
P
C
Q2
1
Lp
Figura 4: Schema di un impianto a vapore
P: pompa, essa realizza la trasformazione adiabatica - isoentropica 1→1’; l’acqua in condizioni di
liquido saturo (punto 1) viene compressa, a spese di un lavoro LP proveniente dall’ambiente esterno,
fino alla pressione di esercizio del generatore di vapore G.V.. Poiché abbiamo un sistema aperto
avremo ∆h = Q − L , con Q = ∫ Tds = 0 , essendo la trasformazione isoentropica e
L = − ∫ vdp = ∆h = h 1' − h 1 .
G.V.: generatore di vapore, viene realizzata la trasformazione isobara (p=cost.) 1’→3; in questa
trasformazione, essendo la pressione costante, risulta δL = −vdp = 0 ⇒ L = 0 , mentre viene
2
fornita la quantità di calore Q1 = h 3 − h 1' . L’energia termica Q1 agisce sul liquido compresso
che diventa prima liquido saturo (2), poi vapore saturo (2’) ed infine vapore surriscaldato (3).
T.V.: turbina a vapore: essa realizza la trasformazione adiabatica - isoentropica 3→4;essendo la
trasformazione isoentropica, risulta Q = 0 , mentre viene compiuto il lavoro L = ∆h = h3 − h4 .
C:
Il vapore surriscaldato ad elevata pressione ed entalpia entra nella turbina a vapore alla
massima temperatura del ciclo T3, ed espande in essa fino alla minima pressione regnante nel
condensatore, con aumento di volume specifico e diminuzione di temperatura. A seguito
dell’espansione viene fornito il lavoro utile Lesp. (lavoro di espansione).
condensatore: si tratta di uno scambiatore di calore dove si realizza la trasformazione isobara isoterma2 4→1; essendo la pressione costante risulta δL = −vdp = 0 ⇒ L = 0 da cui
Q = ∆h ⇒ Q 2 = h 4 − h1 . Nel condensatore viene asportata dal fluido, in condizioni di vapore
saturo quasi secco (punto 4), l’energia termica, non convertita in lavoro, Q2 con conseguente
passaggio del fluido in condizioni di liquido saturo.
Tenendo presente le varie trasformazioni che vengono realizzate nel ciclo possiamo calcolare il
lavoro utile del ciclo limite che risulta:
L u ,lim ite = L esp − L p = (h 3 − h 4 ) − (h1' − h1 )
(III.1.1)
il rendimento limite è allora dato da:
η limite =
L u ,limite
Q1
=
(h 3 − h 4 ) − (h 1' − h 1 )
(h 3 − h 1' )
(III.1.2)
4
Inoltre, il lavoro può essere calcolato facendo riferimento al piano (p,v) come: Lesp. = ∫ vdp e
3
1I
L P = ∫ vdp = v liquido ∆p = v liquido (p1' − p1 ) .
1
Da queste espressioni si vede che in generale LP è trascurabile rispetto a Lesp. ,poiché v liquido è
piccolo3, ma allora L u ,limite ≅ L esp. e quindi per il rendimento si può scrivere:
h3 − h4 h3 − h4
≅
(III.1.3)
h 3 − h 1' h 3 − h 1
A questo punto è utile introdurre i concetti di temperatura media di adduzione di calore Tma e
η limite ≅
temperatura media di sottrazione di calore Tms , definite tramite le relazioni:
h −h
Q
Tma = 1 = 3 1
(III.1.4)
∆s s 3 − s1
Q
h − h1
Tms = 2 = 4
(III.1.5)
∆s s 4 − s1
Facendo riferimento a queste relazioni è possibile esprimere il rendimento del ciclo limite come:
h − h4
T
= 1 − ms
ηlim ite = 3
(III.1.6)
h 3 − h1
Tma
nel nostro caso, poiché la sottrazione di calore avviene a temperatura costante, Tms = T1 .
Un qualunque ciclo può quindi essere rivisto come un ciclo di Carnot tra le temperature Tms e Tma .
2
La trasformazione 3 Æ 4 viene realizzata in modo tale che il punto 4 cada sotto la curva a campana (vapore saturo
quasi secco). Per questo motivo la isobara 4 Æ 1 è anche isoterma.
3
Questo ci dice che in pratica i punti 1 ed 1’ nei piani (T,s) e (h,s) sono quasi sovrapposti, noi li rappresentiamo in quel
modo solo per visualizzare meglio la compressione.
3
III.2) Evoluzione del ciclo limite di un impianto a vapore
Vediamo, in questo paragrafo, come si è evoluto storicamente un impianto a vapore e quali sono
stati i motivi che hanno portato a fare determinate scelte e ad adottare quei particolari accorgimenti
che oggi si ritrovano nei moderni impianti a vapore.
I primi impianti a vapore sono stati utilizzati per la trazione ferroviaria (locomotiva a vapore). In
tali impianti, che sono detti a circuito aperto poiché il fluido (acqua) non viene riutilizzato ma
gettato via nell’atmosfera, non c’è il condensatore e nel ciclo, detto Rankine, il vapore non viene
surriscaldato. È importante osservare che, anche se si parla di circuito aperto, il fluido evolve
seguendo un ciclo, infatti la trasformazione 4→1, che noi comunque rappresentiamo, avviene
nell’atmosfera.
Nel ciclo Rankine l’espansione nella turbina avviene tutta sotto la curva a campana, a differenza di
quanto avviene nel ciclo classico, il vapore umido viene scaricato nell’atmosfera e la turbina a
vapore è sostituita con una macchina alternativa a vapore (v. fig.7).
h
T
2
3
2'=3
20 bar 220°C
1'
2
1
1 bar 100°C
4
1'
4
1
s
s
Figura 5: Ciclo Rankine nel piano (T,s)
Figura 6: Ciclo Rankine nel piano (h,s)
3
2'
GV
2
MA
1'
4
1
Figura 7: Schema dell'impianto di un ciclo Rankine
In genere in questi impianti si raggiungeva una pressione di 20 bar, cui corrisponde una temperatura
di saturazione di T=220° ; nel punto 2, quindi, l’acqua, in condizioni di liquido saturo, ha un
pressione di 20 bar ed una temperatura di 473 K; poiché poi il vapore viene liberato nell’atmosfera
esso si troverà necessariamente, nel punto 4, alla pressione di 1 bar ed alla temperatura di 100 °C
4
(temperatura di saturazione alla pressione atmosferica); pertanto anche assimilando il ciclo Rankine
ad un ciclo di Carnot si vede esso presenta un rendimento bassissimo, risulta infatti:
T
373
ηl = 1 − min . = 1 −
= 0.21
(III.2.1)
Tmax .
473
Appare evidente la necessità di migliorare il rendimento, per far questo bisogna cercare di
allontanare il più possibile le due isoterme; in termini pratici, ciò significa aumentare la temperatura
alla quale forniamo calore al fluido e diminuire la temperatura alla quale sottraiamo calore al fluido.
Innanzitutto vediamo come è possibile abbassare la temperatura alla quale sottraiamo calore e cioè
Tmin ; è chiaro che per far questo non possiamo buttare il vapore nell’atmosfera perché, così
facendo, saremmo vincolati alla pressione atmosferica ed allora introduciamo un condensatore, in
tal modo realizziamo un circuito chiuso, nel quale è possibile ridurre la pressione, e quindi la
temperatura ad essa collegata (siamo in condizioni di saturazione), a valori molto inferiori all’unità.
In tal modo effettuiamo uno scambio di energia in modalità calore a pressioni, e temperature,
minori. Così facendo si passa dai 100 °C della trasformazione 4→1 a 32.5 °C migliorando
sensibilmente il rendimento; risulta infatti:
T
305.5
η l = 1 − min . = 1 −
= 0.35
(III.2.2)
473
Tmax .
4
C
1
Figura 8: Condensatore
Osserviamo che con l’introduzione del condensatore (v. fig.9) la Tmax non è cambiata mentre Tma è
diminuita essendo passati da 1 a 1*. Sperimentalmente però si osserva che la diminuzione di Tma è
più piccola rispetto a quella di Tmin. per cui il rendimento cresce.
T
1*
1
s
Figura 9
Dopo aver ridotto Tmin vediamo come è possibile aumentare Tma ; per far ciò bisogna elevare la
pressione massima (v. fig.10); infatti, già alla pressione di 50 bar corrisponde una temperatura di
saturazione di 550 K= Tmax ; d’altronde aumentando Tmax aumenta Tma e quindi migliora il
rendimento.
5
T
2*
2
1'*
1'
1
s
Figura 10
Il problema, però, è che il punto 4, man mano che si aumenta la pressione e quindi si va in alto nella
curva a campana, si sposta sempre più all’interno della curva e quindi ci troveremmo a lavorare con
un liquido con un titolo troppo basso4 che penalizza parecchio il rendimento della turbina. Il
problema che si presenta non riguarda quindi il ciclo termodinamico ma è un problema tecnico
legato alla turbina vista come elemento meccanico5 .
Per riportare il punto 4 vicino alla curva limite si aggiunge una fase di surriscaldamento nel
generatore di vapore (v. fig.11); in tal modo l’espansione cade fuori la curva a campana e
raggiungiamo valori del titolo, nel punto 4, sufficientemente alti; c’è anche un altro vantaggio
dovuto al fatto che stiamo fornendo calore di elevata qualità (stiamo infatti ad alta temperatura).
Con l’introduzione del surriscaldamento passiamo dal ciclo Rankine, che è possibile caratterizzare
solo tramite la conoscenza di pmin e pmax,al ciclo Hirn, per la cui caratterizzazione è necessaria anche
la conoscenza di Tmax=T3. (vedi pag. 14). Valori tipici, negli impianti classici, sono: p min = 0.05 bar,
p max = 180 bar e Tmax = 550 °C; con questi valori si arriva ad un rendimento limite ηl ≅ 0.44 .
Vediamo però fino a che punto risulta conveniente aumentare la temperatura massima; esiste infatti
un limite dovuto al fatto che se si aumenta troppo Tmax il punto 3 si sposta troppo a destra ed il
fluido, nella turbina, espande tutto nella fase di vapore surriscaldato. Il punto 4 allora cade fuori la
curva, ci troviamo nel punto 4’ (v. fig.11), Tms6 aumenta ed, all’aumentare di Tmsm,, ,diminuisce il
rendimento. Come si vede, quindi, non possiamo aumentare troppo la temperatura poiché bisogna
fare in modo che il punto 4 cada sotto la curva a campana; c’è poi anche un limite tecnologico
all’aumento di temperatura perché, oltre un certo limite, i materiali fondono.
T
3'
3
2
2'
1'
4
1
4'
s
Figura 11
4
Diminuendo il titolo nella miscela liquido – gas aumenta il liquido rispetto al vapore.
In effetti lo stesso problema si presenta anche quando riduciamo Tmin in quanto anche in quel caso il punto 4 si sposta
all’interno della curva a campana.
6
Entra in gioco ora perché la temperatura di sottrazione non è più costante.
5
6
Se non è possibile salire troppo con la temperatura è invece possibile aumentare la pressione di
esercizio del generatore di vapore. Per inciso, si parla di cicli subcritici per pressioni inferiori alla
pressione critica dell’acqua; mentre al di sopra di tale valore si parla di cicli ipercritici.
A parità di Tmax un aumento di pressione produce, come si vede in fig. 12, un aumento di
rendimento, in quanto aumenta Tma , ma si ha anche una diminuzione del titolo perché il punto 3
all’aumentare della pressione, mantenendo Tmax costante, si sposta a sinistra, punto 3’.
Si ripresenta, allora, di nuovo, il problema di un basso valore del titolo che si risolve attraverso il
risurriscaldamento (v. fig. 13).
T
T
3’ 3
T max
3'
2'
4’ 4
2''
3
4'
2
1
4
s
s
Figura 12
Figura 13: Risurriscaldamento
Il risurriscaldamento consiste nel far espandere il vapore in turbina fino ad una certo valore di
pressione intermedia, detta pressione di risurriscaldamento Prisurr. , tale che il fluido sia ancora nelle
condizioni di vapore surriscaldato; poi il fluido viene nuovamente surriscaldato fino alla massima
temperatura del ciclo, e quindi fatto espandere in una seconda turbina fino alla pressione del
condensatore.
Tre un’espansione e l’altra il vapore viene quindi inviato nuovamente nel G.V. ed in particolare nel
surriscaldatore (v. fig.14) . Si vede inoltre che vi sono in tal caso due turbine: una turbina di alta
pressione T.A., nella quale il vapore espande da Pmax a Prisurr. , ed un turbina di bassa pressione T.B.,
nella quale il vapore espande da Prisurr. a Pmin (nella realtà si hanno ulteriori frazionamenti, quindi
negli impianti troveremo una turbina di alta pressione, una di media pressione, ed una di bassa
pressione quest’ultima , a sua volta, può essere realizzata con due corpi per motivi di portata; si
possono avere tuttavia schemi molto più complessi).
2
4'
3
3'
2' 2''
TA
TB
4
1
Figura 14
Con il risurriscaldamento si introduce un altro grado di libertà, rappresentato dalla Prisurr. ; tale
valore viene scelto in base agli altri parametri del ciclo ed in genere si aggira intorno ai 30 bar.
7
Con questo ulteriore accorgimento il rendimento limite arriva a 0.45; a questo punto quindi si vede
che il rendimento aumenta poco anche se le modifiche sono molto complesse da un punto di vista
tecnico.
È possibile poi, per aumentare ancora il rendimento, realizzare più surriscaldamenti; in tal modo il
rendimento cresce, anche se di poco, ma aumentano sensibilmente i problemi tecnici, legati in
particolar modo alle dimensioni delle tubazioni: infatti, a parità di portata massica, al diminuire
della pressione aumenta la portata volumetrica e quindi occorrono delle tubazioni più grandi.
III.3) Andamenti del lavoro utile e del rendimento limite in funzione
della pressione massima del ciclo.
È possibile, in base alle considerazioni fatte nei paragrafi precedenti, andare a diagrammare l’
andamento del lavoro utile del ciclo limite in funzione della pressione massima del ciclo; è evidente
che il lavoro utile dapprima cresce all’aumentare della pressione, perché aumenta il salto entalpico
h 3 − h 4 , ciò lo si può vedere bene nel ciclo Rankine dove all’aumentare di pmax il punto 3 si sposta
in alto (v. fig.5), poi però, dopo un tratto in cui il lavoro si mantiene costante, l’andamento è
decrescente perché aumenta il lavoro di compressione senza che aumenti più il lavoro fornito in
fase di espansione.
Anche l’andamento di Tma in funzione di pmax è dapprima crescente e poi decrescente perché
all’aumentare della pressione diminuisce il tratto 2 → 21 e cioè la quantità di calore fornita ad alta
temperatura.
Per quel che riguarda il rendimento limite, esso è prima crescente ma poi inizia a decrescere,
leggermente, per valori di pmax tendenti al valore critico di pressione (pmax≈221 bar).
Infine è utile diagrammare anche l’andamento del titolo del vapore allo scarico al variare di pmax; a
tal proposito abbiamo detto che conviene, nella macchina reale, che tale valore sia il più possibile
prossimo ad uno, perché usando una T.V. bisogna minimizzare la massa d’acqua liquida rispetto al
vapore.
In fig. 15 sono riportati gli andamenti suddetti per diversi cicli, riassunti nella seguente tabella:
1
2
3
4
5
Ciclo
pmin [bar]
Rankine
Rankine
Hirn
Hirn
Hirn+risurr.
1
0.05
0.05
0.05
0.05
Tmax [°C]
----400
550
550
prisurr. [bar]
--------30
Dalla figura si vede come passando dal ciclo 1 al ciclo 2, cioè introducendo il condensatore,
aumenta sensibilmente il rendimento, aumenta il lavoro utile, mentre diminuiscono, chiaramente, la
Tma , in quanto aumenta la quantità di calore da fornire a bassa temperatura, ed il titolo del vapore
allo scarico, poiché abbassando la retta 4Æ1 il punto 4 si sposta più all’interno della curva a
campana (v. fig.9).
Passando poi al ciclo Hirn (3), surriscaldando cioè il vapore, tutti gli andamenti descritti si spostano
verso l’alto; è da notare però che la Tma è ancora inferiore a quella del ciclo 1 in quanto, come
detto, è rilevante la quantità di calore da fornire al fluido in fase liquida per portarlo in condizioni di
saturazione (è proprio su questo calore che si deve andare ad intervenire se si vuole migliorare il
rendimento come vedremo).
Per il ciclo 4, che presenta rispetto al 3 una maggiore Tmax, gli andamenti si spostano ancora verso
l’alto; infine considerando il ciclo 5, in cui è presente il risurriscaldamento, abbiamo un ulteriore
incremento del rendimento e del lavoro utile, in particolare si vede che il titolo è costante perché,
8
fissati Prisurr. e Tmax , il punto 4 è univocamente individuato, per cui, al variare di pmax , il titolo non
cambia.
Figura 15
Dalla figura si nota infine che il massimo salto di rendimento ∆η si ha con l’introduzione del
condensatore; inoltre il rendimento limite raggiunge al più il valore di 0.45, per incrementarlo
ulteriormente e raggiungere gli attuali valori del rendimento reale bisogna ricorrere alla
rigenerazione.
III.4) Considerazioni sul rendimento. Rigenerazione ideale.
Consideriamo un semplice ciclo Hirn (v. fig.): l’area del ciclo la suddividiamo in tre parti in modo
LI = 12 B I , LII = B I 22 I C I , LIII = C I 2 I 34
L = LI + LII + LIII
tale che
.
(III.4.1)
, con
QI = A12 B, QII = B 22 I C , QIII = C 2 I 3D
Q = QI + QII + QIII
9
T
3
2
2'
II
I
III
1
B'
C' 4
A
B
C D
s
Figura 16
Ciascuna delle tre zone la possiamo vedere come un singolo ciclo termodinamico con un proprio
rendimento, avremo allora:
L
L
L
η I = I , η II = II , η III = III .
(III.4.2)
QI
QII
QIII
Il rendimento complessivo è:
L η I QI + η II QII + η III QIII
=
(III.4.3)
ηl =
Q1
QI + QII + QIII
che può essere interpretato come una media pesata dei rendimenti dei cicli parziali, dove i pesi sono
le quantità di calore fornite QI , QII , QIII .
Si vede allora che per migliorare complessivo η l bisogna migliorare il rendimento dei singoli cicli.
In particolare non si interviene su Tms ,che è la stessa per tutti e tre, ma sulle Tma, che crescono man
mano che ci spostiamo verso destra per cui possiamo certamente affermare che:
η I < η II < η III .
Quindi, quello che penalizza maggiormente η l è η I perciò bisogna cercare di ridurre QI , si tratta
infatti di una quantità di calore fornita a bassa temperatura che alla fine non si può più recuperare.
T
3
2
1
A
5
7
C
6
D
4
B
s
Figura 17
Consideriamo sul ciclo il punto 5 ed effettuiamo, al posto della 3 Æ 4, la trasformazione 3 Æ 5 e
poi la 5 Æ 6 ,parallela alla 1 Æ 2. Così facendo nella trasformazione 5 Æ 6 realizziamo una
sottrazione di calore dal fluido in espansione e c’è una diminuzione di entropia.
Si vede che in termini di area D65B=A12C, d’altronde l’area A12C è, per definizione, pari a QI
per cui il calore sottratto nella 5 Æ 6 è proprio pari a quello che bisogna fornire nella 1 Æ 2.
Possiamo pensare allora di usare una macchina che raccolga questo calore QI nella 5 Æ 6 e lo ceda
nella 1 Æ 2. Stiamo in tal modo realizzando una trasformazione isodiabatica , cosiddetta perché i
10
calori nelle trasformazioni 1 Æ 2 e 5 Æ 6 sono uguali non solo in termini integrali ∫ Tds , ma anche
in termini differenziali (stessa quantità di energia), ciò significa dire che ogni δQ della 5 Æ 6 è
uguale al corrispondente δQ nella 1 Æ 2. In pratica il calore è scambiato tra due corpi praticamente
alla stessa temperatura, tra i quali cioè vi è un dT infinitesimo.
Per come è stata costruita, scambi di calore sotto dT infinitesimi, la trasformazione 5 Æ 6 è
necessariamente reversibile poiché non c’è produzione di entropia legata ad irreversibilità; questo ci
consente allora di rappresentare tale trasformazione nel piano termodinamico e di studiare ancora il
ciclo limite.
In questo modo il rendimento η I non ci penalizza più, in quanto il calore QI non viene fornito
dall’esterno ma è prelevato all’interno del ciclo stesso; per questo motivo si parla di rigenerazione.
A questo punto possiamo scrivere:
I
Q1 = Q II + Q III
(III.4.4)
I
L = L I + L II + L III − ∆L
ma ∆L = LI per cui:
LI = L II + L III .
(III.4.5)
∆L = L54 − L56
(III.4.6)
Infatti possiamo scrivere:
tenendo presente
(h 5 − h 4 )
∆L =
1424
3
trasf. adiabatica rev.⇒ Q = 0
⇒ ∆s = 0 isoentropica
che ∆h = Q − L (prima legge per i sistemi aperti) si ha:
− [∆h 56 − Q 56 ] = (h 5 − h 4 ) − (h 5 − h 6 ) + Q 56 = h 6 − h 4 + Q I = Q I − (h 4 − h 6 ) =
{
1424
3
=Q I
trasf. isoterma e
isobara ⇒ L = 0 e
Q = ∆h
Q I − area (D64B) = area (D65B) − area (D64B) = area (456) = area (127) = L I
In definitiva, visto che gli scambi di calore interno non cambiano il rendimento dei cicli parziali II e
III, il rendimento risulta:
η Q + η III QIII LI
η lI = II II
= I
QII + QIII
Q1
(III.4.7)
Allo stesso risultato si giunge considerando un altro ciclo: possiamo infatti pensare, anziché
eseguire la trasformazione isodiabatica, di spostare il punto 1 nel punto 1* (v. fig.18), in tal modo
noi eliminiamo completamente la quantità di calore QI perché la trasformazione 1*Æ2 è
adiabatica; il rendimento risulta, allora, ancora dato dalla (III.4.7)
T
3
2
1
4
1*
s
Figura 18
11
Teoricamente il problema è risolto, ma nella realtà non esiste una macchina capace di realizzare una
trasformazione isodiabatica, così come non è possibile realizzare la compressione 1*Æ2.
La strada da seguire rimane comunque la stessa anche nel caso reale: eliminare η I con una
rigenerazione, cioè con uno scambio di calore interno, in modo tale che QI non venga preso
dall’esterno ma dall’interno del ciclo stesso.
III.5) Rigenerazione.
La tecnica della rigenerazione consiste nel preriscaldare l’acqua, prima che questa arrivi al
generatore di vapore, utilizzando una certa quantità di vapore spillato dalla turbina. Quindi mentre
con la trasformazione isodiabatica si sottrae una piccola quantità di calore a tutto il vapore in
espansione (tale trasformazione non è però realizzabile in pratica) ora invece si preleva una piccola
quantità di vapore e gli si fa cedere tutto il calore all’acqua in maniera tale da riscaldarla. E’ chiaro
che così facendo da un lato si riduce il calore da fornire al fluido nel generatore di vapore ma
dall’altro diminuisce anche il lavoro di espansione compiuto dal fluido in turbina, perché
diminuisce la portata; complessivamente però si riesce ad avere, entro certi limiti (che
specificheremo più avanti), un aumento del rendimento.
La tecnica della rigenerazione prevede allora l’utilizzo di uno scambiatore di calore a superficie o a
miscela ed inoltre di una seconda pompa (pompa di estrazione). Lo schema dell’impianto è allora il
seguente:
3
2'
GV
2
TV
A
1'
4
Pa
1*
C
1
Pe
Figura 19
1
T
3
2
2'
1'
1*
11
4
1
1*
s
Figura 20
12
La pompa di estrazione, più piccola della pompa di alimento serve a comprimere un po’ il fluido in
maniera da passare dalle condizioni di liquido saturo (punto 1) a quella di liquido (punto 1*). Infatti
fornendo calore a partire dal punto 1 (liquido saturo), si consente il passaggio di fase 1-4, ma non si
va a riscaldare l’acqua, come vorremmo (trasf. 1-2), infatti il passaggio di fase avviene a temp.
costante.
Supponendo lo scambiatore di calore a superficie possiamo schematizzare quello che avviene in
questo modo:
Figura 21
& a spillata dalla turbina ad una entalpia h a e la portata
In ingresso allo scambiatore vi è la portata m
& a ) proveniente dal pozzetto del condensatore ad entalpia h1 , supponiamo infatti m
& co = 1 .
(1 + m
Scriviamo ora l’eq. di bilancio per lo scambiatore nell’ipotesi che sia a controcorrente e che il
vapore proveniente dalla turbina si raffreddi fino a raggiungere l’entalpia h1 ; l’acqua in uscita si
riscalda fino ad una entalpia h 2 R per cui si ha:
& a )(h 2 R − h1 ) = m
& a (h a − h1 )
(III.5.1)
(1 + m
Da questa relazione si ricava:
&a
m
h − h1
= 2R
(III.5.2)
&a
1+ m
h a − h1
da cui:
&a
m
h 2 R = h1 +
( h − h1 )
(III.5.3)
&a a
1+ m
Si nota allora come l’entalpia del fluido in ingresso al generatore di vapore dipende dalla portata
& a e dall’entalpia del fluido di spillamento h a ; in pratica nella nostra
massima del fluido spillato m
equazione vi sono due incognite. Vediamo allora come si procede.
Supponiamo si spillare dalla turbina del vapore surriscaldato, fissiamo cioè il punto A sul ciclo; il
vapore avrà una certa entalpia h a ed una certa pressione p a certamente minore di p 2 .
Esiste un limite alla portata di vapore che conviene spillare; tale limite è dovuto allo scambiatore di
calore.
In esso il vapore dapprima cede calore raffreddandosi fino ad arrivare al punto Av, successivamente
si ha cessione di calore senza variazioni di temperatura per l’intera transizione di fase, fino al punto
Ac, infine il fluido, ormai liquido, continua a cedere calore raffreddandosi fino al punto 1 (la
variazione di temperatura con il vapore ceduto è all’incirca lineare poiché il calore specifico del
13
liquido è all’incirca costante). Nello stesso tempo l’altro fluido entrato nello scambiatore in
condizioni 1 si riscalda in maniera lineare fino a raggiungere in uscita le condizioni del punto 2R.
Diagrammando la temp. dei due fluidi nelle sezioni dello scambiatore, supposto a controcorrente,
abbiamo:
T
A
2Rmax
2R
3
T
AV
A
AL
2
2Rmax
2R Al
ma
1
ma = 0
p2
pa
Av
4
1
Q(x)
s
Figura 22
Figura 23
& a , varia il punto 2R e varia di conseguenza la
Variando la portata massima del fluido spillato, m
pendenza della retta nel diagramma; se si spillasse una portata di vapore infinitesima si avrebbe una
retta orizzontale, la temperatura del punto 2R eguaglia, essendo infinitesima la quantità di vapore
& a aumenta il calore scambiato e
scambiato, la temperatura del punto 1, al crescere della portata m
quindi la pendenza della retta. E’ chiaro che, poiché il flusso termico va dal fluido più caldo al
fluido più freddo, la curva del fluido freddo non può superare quella del fluido caldo per cui al
limite le due curve possono intersecarsi nel punto A V . Questa condizione consiste di determinare la
& aMax ed anche la massima altezza che può raggiungere il
massima portata che conviene spillare m
punto 2R sulla curva a campana 2R Max .
E’ importante osservare che se il liquido proveniente dal condensatore si trova alla pressione p 2
maggiore di quella del fluido spillato p a esso non raggiunge nel punto di intersezione le condizioni
di saturazione anzi, in tal caso, il liquido si riscalda ulteriormente fino a raggiungere T2 RMax .
La temperatura T2 RMax è certamente minore di TA , per quanto detto, da ciò si comprende allora che
il punto 2R Max si troverà comunque al di sotto del punto 2.
La condizione limite che abbiamo ricavato è puramente teorica in quanto esa presuppone di avere
degli scambiatori di superficie infinita; nella pratica non si potrà mai avere in corrispondenza del
punto A V , chiamato “pinch point”, una differenza di temperatura (∆T) nulla ma si avrà sempre un
certo ∆T (intorno alla decina di gradi). È possibile allora affermare, chiaramente con una certa
approssimazione, che la temperatura di uscita del fluido, diretto al generatore di vapore, è all’incirca
pari alla sua temperatura di saturazione alla pressione p a ( T2 R ≅ TS (p a ) ) per cui per quanto riguarda
l’entalpia h 2 R ≅ h S (TS (p a )) ; ciò ci consente di collocare il punto 2R sulla curva a campana in
corrispondenza del punto A l .
14
& a che quindi può essere
Nota l’entalpia h 2 R , nell’equazione di bilancio l’unica incognita è m
facilmente determinata.
& a sul
Vediamo, ora, come influisce la variazione di m
& a aumenta il
rendimento. È chiaro che aumentando m
L
Q1
Q1
calore scambiato, il punto 2R si sposta in alto e di
conseguenza diminuisce il calore che dovrà essere
fornito dall’esterno nel generatore di vapore; al
contempo però diminuisce la portata di fluido che
L
evolve in turbina e quindi diminuisce il lavoro.
Possiamo scrivere:
& a )(h 3 − h1 ) − (1 + m
& a )(h 2 R − h1 )
Q = Q1 − ∆Q = (1 + m
& a )(h 3 − h 4 ) − m
& a (h a − h 4 )
L = L Tot − ∆L = (1 + m
a
infatti dal calore Q1 , che bisogna fornire in assenza di
& a )(h 2 R − h1 )
rigenerazione, si deve sottrarre il calore (1 + m
poiché l’entalpia del fluido in ingresso al generatore di η
vapore non è più h1 ma h 2 R ; mentre dal lavoro
complessivo, che sarebbe fornito se tutto il fluido
espandesse in turbina, bisogna sottrarre il lavoro
& a (h a − h 4 ) perché la portata m
& a lavora in turbina solo per
m
il salto entalpico
(h 3 − h a ) . Nel complesso
il
L
aumenta in quanto il numeratore
rendimento η =
Q1
ma
diminuìsce meno del denominatore.
&a
Il rendimento non aumenta sempre al crescere di m
ma vi è un limite
rappresentato proprio
dal
Q1
&
valore m a ,max che abbiamo ricavato prima.
L
& a ,max succede che il liquido in
Se si supera il valore m
uscita dallo scambiatore e diretto al condensatore
non sarà più alla temperatura del punto 1 con
entalpia h1 ma sarà più caldo. Ciò comporta un inutile
spreco di calore, infatti il lavoro in turbina diminuisce,
perché diminuisce la portata, senza che però vari il
punto 2R e quindi senza riduzione del calore Q1 ; in
ultima analisi ciò si traduce in una riduzione del
rendimento .
Abbiamo visto come varia il rendimento al variare di
& a , vediamo ora cosa succede spostando il punto A.
m
A tal scopo si introduce il grado di rigenerazione R
definito come:
h − h1
R = 2R
(III.5.4)
h 2 − h1
Si tratta di un coefficiente, variabile tra 0 ed 1, che
misura la posizione del punto 2R. In assenza di
rigenerazione h 2 R = h1 ciò implica R=0; mentre al
η
m a,max
ma
η
η
0
R
Figura 24a-b-c-d
15
limite h 2 R = h 2 , quando il punto 2R coincide con il punto 2, e ciò implica R=1. Variando h a tra h 3
e h 4 , possiamo far variare h 2 R tra h 2 ed h1 e quindi R tra 0 e 1.
Possiamo diagrammare l’andamento del rendimento in funzione di R ottenendo la figura 24d,
dove η0 è il rendimento del ciclo in assenza di rigenerazione. Tale curva è costruita variando il
& a ,max che rende massimo il rendimento.
punto A e considerando per ogni posizione di A il valore m
Si vede che inizialmente il rendimento cresce ma poi si raggiunge un limite a partire dal quale il
rendimento inizia a diminuire. In base a quanto detto all’aumentare di R il punto 2R si sposta verso
l’alto e quindi aumenta la temperatura media di adduzione di calore Tma dunque in base alla
T
relazione η = 1− ms , essendo invariato Tms , il rendimento dovrebbe essere sempre crescente. La
Tma
contraddizione è solo apparente perché a relazione considerata è valida solo per trasf. reversibili,
mentre nel nostro caso lo scambio di calore nello scambiatore è un processo irreversibile che
avviene con produzione di entropia.
Per trasformazioni reversibili abbiamo Q1 = Tma ∆S e Q 2 = Tms ∆S da cui, essendo uguali le
variazioni di entropia:
T
L Q 2 − Q1
Q
= 1 − 2 = 1 − ms
η=
=
(III.5.5)
Q1
Q1
Q1
Tma
Nel caso ideale di trasformazioni isodiabatica non si ha produzione di entropia poiché gli scambi
termici avvengono sotto ∆T infinitesimi, nel nostro caso invece lo scambio termico nello
scambiatore avviene sotto un V finito. Risulta allora chiaro che quanto più è alta la temperatura del
vapore spillato dalla turbina tanto più alta è la produzione di entropia che va ad invertire la tendenza
crescente del rendimento.
Una volta capito il problema risulta semplice trovare una soluzione: la soluzione tecnica che si
adotta è quella di andare a compiere più spillamenti in punti diversi della turbina in modo da ridurre
i salti termici nello scambiatore e quindi la produzione entropica (il vapore più freddo riscalda il
fluido a partire dalla temperatura del punto 1 e poi man mano, il vapore a temperatura via via più
alta riscalda il fluido già preriscaldato). In teoria converrebbe avere un impianto con un numero
infinito di spillamenti, in tal caso, infatti, si ha un rendimento sempre crescente e per R=1 si ottiene
L + L III
il rendimento limite η = II
dal quale siamo partiti, ottenuto con una trasformazione
Q II + Q III
isodiabatica; nella pratica però ci si ferma a 7÷8 spillamenti.
Figura 25
16
A questo punto occorre precisare che, quando si adotta la tecnica della rigenerazione, il piano (T,s),
dove s è l’entropia specifica, non è più idoneo a rappresentare il ciclo termodinamico svolto dal
fluido ma si deve considerare il piano (T,S), con S entropia totale pari all’entropia specifica s
moltiplicata per la massa di fluido presente nel circuito principale dell’impianto. Supponendo, come
prima, che la portata di vapore che va al condensatore sia pari ad 1kg/s, mentre quella spillata sia
& a kg/s, nel piano (T,S) si dovranno considerare due curve a campana; una relativa ad 1 + m
&a
pari a m
kg/s di fluido ed una relativa ad 1 kg/s. La rappresentazione del ciclo è allora la seguente:
Figura 26
& a dunque, mentre l’entropia specifica per il vapore presente in
Nel punto 5 viene spillata la portata m
turbina non muta, quella totale diminuisce passando da S5 = (1 + M a )s 3 ad S5' = 1⋅ s 3 , mettendo con
ciò a disposizione per il riscaldamento dell’acqua la quantità di calore Q = T5 ⋅ M a ⋅ s 3 pari all’area
C5’5D. Tale quantità di calore consente il riscaldamento dell’acqua da T1 a T2 R (per effetto della
rigenerazione l’acqua arriva al generatore di vapore ad una temperatura compresa tra 200°C e
300°C). naturalmente, poiché la portata di vapore rimasto in turbina è pari ad 1 kg/s, il ciclo deve
fare a questo punto riferimento alla curva a campana relativa ad 1 kg/s di fluido; si raggiunge così il
& a dopo aver ceduto calore viene reinserita nell’impianto a valle del
punto 1. La portata m
& a kg/s di fluido.
condensatore per cui si ritorna al punto 1’ sulla curva relativa ad 1 + m
Con questa rappresentazione possiamo quindi vedere immediatamente il calore scambiato e la
variazione di entropia totale avutasi con lo spillamento.
17
Nel caso in cui vi sono più spillamenti bisogna andare a considerare una curva a campana diversa
per ogni spillamento per cui alla fine si avrà un diagramma del tipo:
Figura 27
In questo modo risultano evidenti le variazioni di entropia totale nei vari spillamenti.
Un’ulteriore considerazione da fare quando si parla di rigenerazione è relativa alla potenza utile che
si ritrova all’asse della turbina; è chiaro infatti che a causa dei vari spillamenti tale potenza si
riduce.
In assenza di spillamenti la potenza utile all’asse è:
& v ∆h is ηit ηm
Pua = m
(III.5.6)
dove:
& v è la portata di vapore in turbina;
m
∆h is è la variazione di entalpia considerando l’espansione in turbina isoentropica;
ηit è il rendimento interno di turbina;
ηm è il rendimento meccanico.
La quantità ∆h is ηit è pari alla variazione di entalpia reale ∆h r .
&j
Considerando ora N spillamenti e supponendo che in ognuno di essi si prelevi la portata m
avremo:
N
& GV = m
& CO + ∑ m
&j
m
(III.5.7)
j=1
& GV è la portata al generatore di vapore e m
& CO è la portata al condensatore.
dove m
18
La potenza utile all’asse risulta allora:
N
& CO ∆h is + ∑ m
& j∆h j )ηit ηm
Pua = (m
(III.5.8)
j=1
& j subisce in turbina prima di essere
dove ∆h j = h 3 − h j è la variazione di entalpia che la portata m
spillata (contributo al lavoro).
In modo del tutto equivalente si può scrivere:
N
& GV ∆h is − ∑ m
& j∆h ' j )ηit ηm
Pua = (m
(III.5.9)
j=1
& j non ha subito in turbina
dove ∆h ' j = h j − h 4 rappresenta la variazione di entalpia che la portata m
(lavoro perduto).
In genere Pua si esprime come:
& CO ∆h is (1 + ε)ηit ηm
Pua = m
(III.5.10)
dove ε è dato dalla relazione:
N
ε=
∑ m& ∆h
j=1
j
j
& CO ∆h is
m
Per avere un’idea sugli ordini di grandezza, in genere risulta
(III.5.11)
∑ m&
j
& CO ed ε ≅ 25 ÷ 30% .
≅ 50%m
& GV gli spillamenti riducono la
Se si tiene presente la relazione (III.5.9) si vede che a parità di m
potenza.
& CO gli spillamenti
Se invece si tiene presente la relazione (III.5.8) si vede che a parità di m
& CO è limitato dalla
consentono addirittura di aumentare la potenza. Nella realtà infatti il termine m
massima portata che è in grado di sopportare la turbina di bassa pressione per cui, in assenza di
& GV = m
& CO non può superare questo limite; gli spillamenti ci consentono, invece,
spillamenti, m
& CO , di aumentare m
& GV aumentando in tal modo le portate nelle turbine di alta e
mantenendo fisso m
media pressione, che ancora non erano al limite; questo si traduce in ultima analisi in un aumento di
Pua come si desume dalla relazione (a).
Consideriamo ora il consumo specifico di vapore ( Cs ) definito come:
Cs =
&v
m
Pua
t
hMW
(III.5.12)
Dall’espressione della potenza in assenza di spillamenti si ricava:
Cs =
1
≅ 2.5
∆h is ηit ηm
t
hMW
(III.5.13)
Con gli spillamenti se si fa riferimento alla relazione (a) si raggiunge un Cs ≅ 3 se invece si fa
riferimentoalla relazione (b) si ha un Cs ≅ 2 . A titolo di esempio per avere un’idea degli ordini di
grandezza delle portate supponiamo di avere un impianto di potenza 320 MW, prendendo Cs ≅ 2 ,
& CO pari a circa 640 t/h e di una portata
abbiamo bisogno di una portata di vapore al condensatore m
d’acqua di raffreddamento pari a circa 32000 t/h.
19
In conclusione si riporta lo schema di un impianto con più spillamenti.
Figura 28
Passiamo a questo punto ad analizzare più in dettaglio i vari componenti dell’impianto trascurando,
per il momento, la turbina a vapore ed il generatore di vapore cui in seguito sono dedicati altri
capitoli.
III.6) Condensatore.
Il condensatore è uno scambiatore di calore che permette di
sottrarre calore al vapore e cederlo all’acqua di raffreddamento.
Il fluido passa dalle condizioni di vapore umido ad alto titolo
(~ 0.90) a quelle di liquido saturo a T=cost. (infatti, T4=T1).
4
C
1
mv
Lo scambio di calore avviene attraverso tre meccanismi in serie:
•
•
•
mH2O
Convezione vapore - parete;
Conduzione attraverso la parete;
Convezione parete - acqua di raffreddamento;
Figura 29
Andando ad esaminare i coefficienti di scambio termico, si vede che prevale il terzo termine
essendo esso di un ordine di grandezza maggiore degli altri.
20
Scriviamo l’equazione d’equilibrio termico per il condensatore:
& v ⋅ (h4 – h1) = m
& H 2O ⋅ c ⋅ (Tu – Ti)
m
(III.6.1)
il termine (h4 – h1) può essere scritto come (r⋅x) dove r è il calore latente d’evaporazione alla
temperatura Tv; mentre x è il titolo.
Alla pressione di 0.05 bar (cui corrisponde T = 32.5 °C) r è circa 570 Kcal / Kp e poiché x ≈ 0.9,
allora (h4 – h1) ≈ 510 Kcal/Kg; questo termine dunque è fisso ed anzi abbiamo cercato di elevarlo il
& v è invece legato alla potenza dell’impianto, dunque fissata la potenza
più possibile. Il termine m
&v .
che l’impianto deve fornire è fissata m
Ciclo HIRN
T
3
2
2'
1'
1
x
4
r
s
Figura 30
A questo punto, dall’equazione d’equilibrio termico, si vede che abbiamo due possibilità per
realizzare lo scambio termico tra il vapore e l’acqua di raffredamento:
1. Adoperare una piccola portata d’acqua, sottoposta ad un elevato ∆T;
2. Adoperare una gran portata d’acqua; sottoposta ad un basso ∆T.
Per giustificare la scelta che effettuiamo, consideriamo il diagramma che segue.
T
L’acqua di raffreddamento, entra nel condensatore alla
Tv
temperatura
Ti (è fissa) alla quale si trova il corso
Tu
d’acqua a disposizione, riceve calore dal vapore e si
riscalda. La quantità di calore che deve essere scambiata
per portare il vapore al punto 1, nelle condizioni di
liquido saturo, è pari a (h4 – h1); dunque l’acqua di
α
raffreddamento uscirà dal condensatore alla temperatura
Ti
Tu.
h4 h1
Figura 30
Poiché la cessione di calore avviene dal vapore all’acqua,
Tv > Tu, allora quanto più grande è Tu tanto più grande sarà Tv; ma ciò va a peggiorare il rendimento
del ciclo limite. Quindi poiché il nostro scopo è ridurre il più possibile Tv , bisogna necessariamente
abbassare Tu ed essendo Ti fisso, ciò comporta un piccolo ∆T e di conseguenza la necessità di
impiegare grosse portate d’acqua. E’ giustificata in tal modo la scelta della seconda possibilità.
Per inciso c’e da dire che il valore massimo di ∆T è fissato dalle norme le quali impongono
(Tu – Ti) < 10 °C per motivi d’impatto ambientale.
Dalla fig. 30 si vede che ridurre Tu significa avere tg(α) piccolo, infatti risulta:
tgα =
&
Tu − Ti
m
≅ CO
& H 2O
h 4 − h1 m
(III.6.2)
21
per cui bisogna avere una portata d’acqua molto maggiore di quella di vapore; in genere:
& H 2O ≅ 50 ⋅ m
& CO
m
(III.6.3)
Facciamo un rapido calcolo.
& v/
Supponiamo di volere una potenza di 1.000 MW, poiché il consumo specifico di vapore ( Csv = m
& v di 2.000 [t/h] e di
P [t/(hKW)] ) è all’incirca 2, abbiamo bisogno di una portata di vapore m
conseguenza necessiteremo di una portata d’acqua di 100.000 [t/h]; questo è il motivo per cui le
centrali si costruiscono in prossimità dei fiumi o del mare. Si comprende anche che sarebbe comodo
avere una Ti più piccola possibile.
Dal discorso fatto si capisce come i termini che ci consentono di portare il fluido a bassa pressione
& H 2O e Ti, mentre la geometria interna del
(~ 0.05 bar) e bassa temperatura (32.5 °C) sono m
condensatore non interviene in alcun modo.
La geometria del condensatore interviene invece nella relazione:
& H 2O ⋅ c ⋅ (Tu – Ti) = hcond. ⋅ Acond. ⋅ (Tv – T m& H2O )
m
(III.6.4)
dove:
hcond. = coefficiente di scambio termico;
Acond. = superficie di scambio termico;
Tv = temperatura media del vapore (costante);
T m& H2O = temperatura media dell’acqua.
Dalla (III.6.4) si vede che usando, al limite, un condensatore per il quale hcond. = ∞ e Acond. = ∞ si
avrà in uscita Tv = Tu, cioè il vapore si trova alla stessa temperatura d’uscita dell’acqua (∆T=0).
E’ importante, a questo punto, evidenziare che è il condensatore a fissare le condizioni
termodinamiche del punto 4, cioè pressione e temperatura, e non la turbina; la turbina avverte
semplicemente le diverse condizioni dei punti 3 e 4 e sviluppa lavoro in base a tali valori.
Sempre per quanto riguarda il condensatore c’è da notare inoltre che esiste una notevole differenza
di pressione fra l’interno (0.05 bar) e l’esterno (1 bar) del condensatore e che a causa di ciò entrerà
al suo interno una piccola quantità d’aria.
Quest’aria produce due effetti negativi:
1. aumenta la pressione all’interno del condensatore e ciò influisce negativamente sul
rendimento;
2. crea pericoli in fase di combustione;
è quindi necessario eliminarla.
Si utilizza allora un componente, l’EIETTORE, che consente di mantenere la pressione desiderata
all’interno del condensatore; l’aria però non è espulsa dall’eiettore ma è eliminata definitivamente
da un altro componente che è il DEGASATORE (v. par. III.7).
L’eiettore è costituito da un tubo convergente – divergente nel quale è convogliato del vapore
prelevato prima dell’ingresso della turbina. A causa della forma particolare del componente (a
proposito cfr. cap. V) tale vapore esce da esso ad una pressione inferiore di quella presente
all’interno del condensatore, per cui l’aria è risucchiata da quest’eiettore dove si mescola al vapore.
In queste condizioni, l’aria non è buttata via perché è miscelata a vapore d’elevata qualità (vapore
ad alta pressione e temperatura); il fluido è quindi rallentato a valle dell’eiettore ed è inviato in uno
scambiatore a rigenerazione dove va a riscaldare dell’acqua.
22
Abbiamo visto, in precedenza, il motivi per cui le centrali d’elevata potenza sono costruite in
prossimità di corsi d’acqua in modo da avere a disposizione la necessaria quantità d’acqua di
raffreddamento da inviare al condensatore; tuttavia vi sono casi (I. V. di piccola potenza) in cui gli
impianti sono costruiti senza avere a disposizione portate naturali, ed elevate, d’acqua.
In tal caso si ricorre ad un’altra tecnica, che prevede l’utilizzo della torre di raffreddamento.
Figura 31
L’acqua di raffreddamento circola in un circuito chiuso: essa passa nel condensatore dove si
riscalda, poi è inviata alla torre di raffreddamento dove è polverizzata e fatta raffreddare a contatto
con l’aria.
Nel processo di raffreddamento una certa quantità d’acqua evapora, per cui è necessaria una piccola
integrazione.
Utilizzando questa tecnica non si riescono ad ottenere ∆T piccoli (il ∆T si attesta intorno ai 20 °C),
come nel caso dei circuiti di raffreddamento per impianti a vapore d’elevata potenza, per cui è
chiaro che il fluido in uscita dal condensatore si troverà a temperatura più elevata.
Essendo allora Tms maggiore, il rendimento limite peggiora (diminuisce). Tale soluzione è pertanto
adottata per impianti a vapore di piccola potenza, che non richiedono valori elevati di rendimento,
potendoli così costruire lontano da corsi d’acqua.
III.7)Scambiatori Rigenerativi
Quando in un impianto vi sono più spillamenti (7-8) alcuni rigeneratori sono collocati a monte della
pompa d’alimento e si parla di rigeneratori di bassa pressione; gli altri invece, posti a valle, sono i
rigeneratori di alta pressione.
Nei rigeneratori di bassa pressione il vapore che serve per riscaldare l’acqua è spillato dalla turbina
di bassa pressione e può essere prelevato sia in condizioni di vapore leggermente surriscaldato, sia
come vapore umido.
Il rigeneratore si presenta, allora, come un semplice scambiatore a superficie costituito da un fascio
di tubi attraversati dall’acqua e contenuti in un corpo cilindrico nel quale arriva il vapore dallo
spillamento e dal quale fuoriesce la relativa condensa (v. fig.32).
23
Figura 32
L’ultimo rigeneratore prima della pompa di alimento è il degasatore (v. fig 33): si tratta di uno
scambiatore a miscela che contribuisce ad espellere l’aria entrata nel circuito e miscelatasi al
vapore.
L’aria estratta dal condensatore tramite l’eiettore è, infatti, riportata nel circuito e vi è la necessità
di eliminarla per evitare il fenomeno del feam boinding (v. fig.28)
Figura 33
Per le leggi che regolano il contenuto di gas disciolti in un liquido, e per la possibilità di far
scaricare spontaneamente nell’atmosfera l’aria che si libera dall’acqua è conveniente realizzare la
degasazione a temperature superiori ai 100 °C e quindi a pressioni superiori a quella atmosferica
ecco il motivo per cui il degasatore è posto appena prima della pompa di alimento (bassa pressione
e più alta temperatura). Il degasatore è posto, poi, in alto ad una quota di diversi metri per evitare
che la pompa di alimento vada in cavitazione.
Nel degasatore si fanno venire a contatto, in controcorrente, l’acqua più o meno polverizzata ed il
vapore proveniente da uno spillamento; l’acqua allora si riscalda condensando il vapore mentre si
libera gran parte dell’aria ancora disciolta in essa. L’acqua degasata è raccolta in un serbatoio che fa
da polmone.
24
In concomitanza all’aria è espulsa anche una certa quantità di vapore, questa si somma alle
inevitabili perdite presenti nell’impianto ed al vapore che volutamente si fa fuoriuscire in alcuni
punti per ragioni tecniche (quali la constatazione che nei tubi circoli effettivamente solo vapore,
questa valutazione è fatta aprendo delle valvole di controllo); si presenta quindi l’esigenza di una
piccola integrazione d’acqua.
III.8)Pompa di alimento
Nei grandi impianti a vapore l’incremento di pressione non viene realizzato con un’unica pompa ma
attraverso schemi più complessi.
Ad esempio per un impianto da 320 MW si hanno tre gruppi in parallelo e per ogni gruppo ci sono
due pompe in serie: il Booster e la Pompa di alimento .
Alla pompa di alimento si richiedono, infatti, diverse caratteristiche che
non è possibile coniugare in un unico organo; la pompa, infatti, deve
realizzare grossi incrementi di pressione (grande prevalenza), deve essere
in grado di smaltire grosse portate e non deve andare in cavitazione.
Le pompe che hanno una grossa prevalenza, però, non riescono in genere
smaltire ingenti portate per questo motivo, quindi, si ricorre a più gruppi
in parallelo.
In tal modo, infatti, la portata di ciascun gruppo è ridotta, nell’esempio
ogni gruppo ha una portata pari ad 1/3 di quella complessiva.
Per evitare, poi, il problema della cavitazione si dispone prima della
pompa di alimento, in ciascun gruppo, un Booster. Si tratta di una pompa,
espressamente progettata per non andare in cavitazione che realizza un
piccolo incremento di pressione necessario ad evitare che vada in cavitazione la pompa di alimento.
Figura 34
Booster e pompa sono mossi da un motore
elettrico(v. fig.35); è presente, inoltre, prima
della pompa di alimento un variatore di velocità
che consente la variazione di velocità della
pompa di alimento e conseguentemente della
portata di vapore.
& v ⋅ ∆h è chiaro
Ciò permette di regolare la potenza sviluppata dall’impianto; infatti, essendo P = m
& v.
che per effettuare la regolazione si va ad agire su m
Figura 35
25









