Congruenze e Similitudini

Capitolo 4
Congruenze e Similitudini
4.1
Congruenze
Sulla superficie sferica continuano a valere i ben noti criteri di congruenza dei
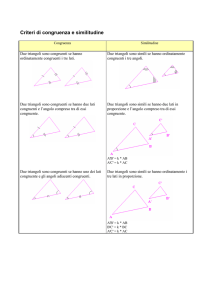
triangoli piani. Precisamente, due triangoli sferici che hanno ordinatamente
uguali (ossia della stessa misura):
• un lato e i due angoli adiacenti (ALA)
F
C
<)cb= 44,57°
G
|EF|= 0,91
A
<)ca= 57,53°
|AB|= 0,91
B
<)ca= 57,53°
<)cb= 44,57°
E
• due lati e l’angolo compreso (LAL)
F
G
C
|AC|= 0,59
|EF|= 0,91
|EG|= 0,59
A
<)ca= 57,53°
<)ca= 57,53°
E
|AB|= 0,91
B
4.1 Congruenze
23
• tre lati (LLL)
C
|AC|= 0,59
|CB|= 0,73
A
|EG|= 0,59
G
E
|AB|= 0,91
B
|GF|= 0,73
|EF|= 0,91
F
hanno tutti gli altri elementi uguali. Da notare che due triangoli congruenti
possono non essere sovrapponibili, né con un movimento rigido sulla sfera,
né con uno simile nello spazio! Basta pensare ad un triangolo sferico scaleno
ottenuto da un altro per “riflessione” in una “retta”, attribuendo a questi
termini il loro significato nell’ambito della geometria sferica.
Oltre ai precedenti criteri ne vale però un quarto (denotato con AAA):
• due triangoli sferici sono congruenti se hanno angoli corrispondenti
uguali
C
<)ba= 91,12°
A
<)ca= 57,53°
B
F
<)fg= 44,57°
<)cb= 44,57°
<)fe= 57,53°
E
G
<)eg= 91,12°
In altre parole, sulla sfera non esistono triangoli simili differenti! Di
un oggetto (figura) sulla sfera non è quindi possibile realizzare, sulla stessa
sfera, una rappresentazione in scala!
4.2 Similitudini
4.2
24
Similitudini
Possiamo costruire poligoni simili ma diversi sulla superficie sferica?
NO! Il concetto di similitudine non può essere trasferito sulla sfera: ad
esempio due triangoli sferici simili devono essere uguali! Sulla sfera infatti,
dare l’ampiezza di tre angoli o la lunghezza di tre lati consente di costruire la
figura, risolvendo completamente il problema. Per esempio se sulla superficie
sferica prendiamo due triangoli regolari non congruenti, allora gli angoli del
primo saranno diversi da quelli del secondo.
C
C
<)cd= 80°
<)cd= 70°
|BC|= 1,02
|CA|= 1,02
|CA|= 1,42
|BC|= 1,42
<)ad= 70°
<)ac= 70°
<)ac= 80°
A
<)ad= 80°
A
|AB|= 1,42
B
|AB|= 1,02
B
Consideriamo ora un poligono con quattro lati. Sul piano, se angoli
corrispondenti di due quadrangoli sono congruenti, allora lati corrispondenti
sono proporzionali. Questo non è vero sulla superficie sferica!
<)df= 120,1°
<)cf= 90°
<)ac= 90°
<)ad= 90°
<)eb= 90°
<)cb= 90°
<)ge= 120,02°
<)gc= 90°
Possiamo costruire
goli con angoli di
ma che non sono
no nessuna coppia
proporzionali!
infatti due quadran90◦ , 90◦ , 90◦ , 120◦ ,
simili, che non handi lati corrispondenti