NMR dinamico

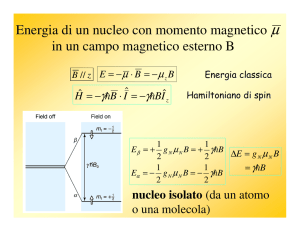
Cinetica Chimica - NMR dinamico
Chimica Fisica Industriale Modulo B
Annalisa Bisello, Saverio Santi
Esperienza n°3
NMR dinamico
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Introduzione
Proprietà dei nuclei. La materia è fatta di atomi. Gli atomi sono costituiti da elettroni e da nuclei ed
ogni nucleo atomico possiede quattro importanti proprietà fisiche:
 massa
 carica elettrica
 magnetismo
 spin
I bosoni (così chiamati in onore del fisico indiano Satyendra Nath Bose) sono particelle che
formano stati quantici compositi totalmente simmetrici. Il teorema di Bose-Einstein enuncia che
essi hanno spin intero e che non esiste proprietà di esclusione per i bosoni, che sono liberi di
occupare lo stesso stato quantico. I bosoni elementari agiscono come portatori delle forze
fondamentali.
I fermioni (in onore di Enrico Fermi) sono particelle che formano stati quantici compositi
totalmente antisimmetrici. Di conseguenza i fermioni sono soggetti al principio di esclusione di
Pauli "non più di un fermione può occupare un singolo stato quantico" e obbediscono alla statistica
di Fermi-Dirac. Il teorema dello spin statistico enuncia che i fermioni hanno spin semi-intero.
Tutte le particelle elementari si dividono in fermioni e bosoni; tuttavia anche particelle composte da
un insieme di altre particelle (come i nuclei atomici 2H (deuterio) e 14N) possono essere fermioni o
bosoni, a seconda del loro spin totale.
A seconda che abbia spin intero (bosone) o semi-intero (fermione) una particella può allora
possedere due tipi di momento angolare:
-un momento angolare “convenzionale” derivante dal suo moto. Per esempio, un elettrone in un
atomo può avere un momento angolare orbitalico dovuto al suo moto intorno al nucleo. Tale moto è
associato ad un numero quantico intero di momento angolare ed ha le proprietà di un momento
angolare di una molecola ruotante;
Figure 3.1
-un momento angolare di spin, “intrinseco” che è una proprietà della “natura” dell’elettrone ed è
sempre uguale e cioè spin = ½.
42
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Spin nuleare e risonanza
La spettroscopia NMR è basata sull’interazione tra un momento magnetico di spin nucleare e un
campo magnetico. I nuclei di tutti gli atomi sono caratterizzati da un numero quantico di spin
nucleare, I, che può essere maggiore o uguale a zero ed è sempre multiplo di ½. I nuclei con I = 0
non possiedono spin nucleare e quindi non possono essere studiati via NMR e sono detti NMR
silenti.
isotopo
abbondanza
naturale
spin
Rapporto giromagnetico
γ/rad s–1 T-1
Frequenza di
Larmor (MHz)
B0 = 4.7 T
1
H
99.98%
1/2
267.5 × 106
-200
2
H
0.015%
1
41.1 × 106
-30.70
B
19.9%
3
28.7 × 106
-21.49
12
C
98.9%
0
-
-
13
C
1.1%
1/2
67.2 × 106
50.29
14
N
99.6%
1
19.3 × 106
-14.45
15
N
0.37%
1/2
-27.1 × 106
+20.27
16
O
99.96%
0
-
-
17
O
0.04%
5/2
-36.3 × 106
+27.11
F
100%
1/2
251.8 × 106
-188.15
Na
100%
3/2
70.8 × 106
-52.90
100%
5/2
69.8 × 106
-52.12
P
100%
1/2
108.4 × 106
-81.04
Co
7/2
100
6.3316
-47.23
½
100
-0.84677
+48.95 10-5
½
33.80
5.8385
-16.80 10-3
10
19
23
27
Al
31
59
103
Rh
195
Pt
Tabella 3.1

I nuclei con I ≠ 0 possiedono momento angolare, I , e ovviamente carica. Il moto di questa carica

dà origine a un momento magnetico associato, µ :


µ =γ ×I
43
(3.1)
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
dove il termine γ è il rapporto giromagnetico che è costante per un dato nucleo e può essere
considerato come una misura di quanto "magnetico” è il nucleo. Sia il momento angolare che il
momemto magnetico sono quantità vettoriali e possiedono quindi direzione e modulo. Quando si
applica un campo magnetico statico, B0, i momenti magnetici nucleari si allineano al campo in un
numero discreto di orientazioni poichè gli stati energetici coinvolti sono quantizzati (Zeeman
splitting). Per uno spin avente numero quantico magnetico I sono possibili (2I + 1) orientazioni
rispetto a una direzione di riferimento, solitamente l’asse z. Queste possibili orientazioni sono gli
autovalori (in unità ħ) dell’operatore proiezione secondo z del momento angolare Iz e sono definiti
dal numero quantico mI, che può assumere valori mI = I, (I – 1), (I – 2)…(-I):
Iz = ħmI
(3.2)
Per esempio per il protone che possiede I = 1/2, ci sono 2 possibili stati, con valore +1/2 e –1/2 e le
corrispondenti autofunzioni vengono indicate con α e β:
Izα = +1 / 2α
µ zα = +1 / 2γ N α
(3.3)
Izβ = −1 / 2β
µ Z β = −1 / 2γ n β
(3.4)
Energia
Nel caso del deuterio invece dove I = 1, sono possibili tre diverse orientazioni con mI = +1, 0, -1.
-1/2
-1
1/2
1
0
I=1
I=1/2
Figura 3.2
L’effetto del campo magnetico sul momento magnetico può essere descritto in termini di meccanica
classica che permette una più facile visualizzazione dei fenomeni coinvolti. Un sistema avente
momento magnetico µ, posto in un campo magnetico B0 è soggetto ad una forza torcente che
provoca un moto di precessione del momento magnetico attorno alla direzione individuata da B0
con velocità angolare, nota come frequenza di Larmor ωL, definita dalla relazione:
44
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
ωL = -γB0 rad s-1
νL = -γB0/2π Hz
oppure
(3.5)
ωL = 2πνL
Figura 3.3
Questo movimento è analogo al moto di un giroscopio nel campo gravitazionale terrestre. La
direzione del moto è determinata dal modulo e dal segno di γ che può essere in senso orario o
antiorario, ma è sempre lo stesso per un dato nucleo.
1
15
H
γ>1
E
27
N
Al
γ<1
-1/2
E
E
+1/2
−1/2
+1/2
H
H
−1/2
−3/2
−1/2
+1/2
+3/2
+5/2
H
Figura 3.4
La risonanza magnetica avviene quando il nucleo cambia il suo spin assorbendo un quanto di
energia. Questa energia viene applicata come radiazione elettromagnetica, la cui frequenza coincide
con quella della precessione di Larmor:
∆E = hνL = hγB0/2π
45
(3.6)
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Per il protone , il cui spin è ½, in presenza di un campo magnetico statico, l’orientazione parallela al
campo applicato, α, è leggermente a più bassa energia di quella con orientazione antiparallela, β,
quindi all’equilibrio vi sarà un eccesso di nuclei nello stato α come definito dalla distribuzione di
Boltzmann:
Nα
∆E / RT
=e
Nβ
(3.7)
dove Nα,β rappresentano il numero di nuclei alla data orientazione di spin, R la costante dei gas, T la
temperatura. La differenza di energia tra i livelli di spin è piuttosto piccola e quindi le
corrispondenti differenze di popolazione sono altrettanto piccole. Questo è il motivo per cui la
spettroscopia NMR è una tecnica meno sensibile rispetto all’IR o all’UV. L’eccesso di popolazione
di spin nucleari può venire rappresentata come un insieme di spin distribuiti in modo casuale su un
cono di precessione il cui asse è parallelo all’asse z. La differenza di popolazione dei due stati di
spin dà origine a un vettore di magnetizzazione totale M0 diretto lungo l’asse z, mentre lungo la
direzione trasversale non ci sono orientazioni predefinite degli spin e quindi la magnetizzazione nel
piano trasversale è nulla.
z
z
M0
x
x
y
y
Figura 3.5
FT-NMR (a impulsi)
La condizione principale per indurre transizioni tra i livelli energetici è l’applicazione di un campo
magnetico dipendente dal tempo oscillante alla frequenza di Larmor ωL. Questo campo è fornito
dalla componente magnetica del campo di radiofrequenze applicato, che viene definito come B1.
Esso è trasmesso attraverso una bobina che circonda il campione la cui geometria è tale che il
campo B1 sia parallelo al piano trasversale e perpendicolare alla direzione data dal campo statico B0.
46
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Esso può venire anche pensato come un campo rotante nel piano xy con componenti B1x = B1senωt e
B1y = −B1cosωt. La descrizione dei processi, che avvengono durante un esperimento NMR risulta
semplificata se ci si riferisce ad un sistema di assi rotanti intorno all’asse z con frequenza angolare
ω, cioè con la stessa frequenza e verso di B1. Nel nuovo sistema di riferimento la direzione del
campo magnetico B1 può essere scelta come l’
asse rotante x’ e quindi questo risulta fisso. In
presenza del solo campo magnetico statico gli spin nucleari precedono lungo l’asse z e la
magnetizzazione M0 risulta fissa nel sistema rotante. Se è presente anche il campo magnetico
oscillante B1 nel sistema rotante la magnetizzazione precederà attorno a B1, cioè ruoterà nel piano
z’y’ perpendicolare a x’. Negli esperimenti pulsati o a trasformata di Fourier (FT) il campo
magnetico B1 viene applicato per un periodo di tempo molto breve (impulso). Durante questo
tempo, τp, la magnetizzazione sarà ruotata attorno all’asse di precessione di un angolo θ = ωτp e
avrà una componente nel piano x’y’. Se θ = π/2 e ω = ωL la magnetizzazione sarà orientata lungo
l’asse y’.
z
z
M0
M0
B1
M0
B1
B1
x
x
y
z
z
y
impulso di angolo θ
B1 M
0
x
y
impulso di angolo 90°
x
y
impulso di angolo 180°
Figura 3.6
L’azione dell’impulso a radiofrequenza su un campione all’equilibrio termico perturba il sistema di
spin da questo stato e una volta interrotto il campo a radiofrequenza il sistema tenderà a ristabilire le
condizioni di equilibrio perdendo l’eccesso di energia fornito dall’impulso. La variazione della
magnetizzazione lungo la direzione z corrisponde a un cambio della popolazione degli spin, il
z
x
z
y
x
z
y
x
Figura 3.7
47
z
y
x
y
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
ripristino della magnetizzazione lungo questa direzione definito rilassamento longitudinale o spinlattice, corrisponde al ritorno della popolazione di spin all’equilibrio e quindi alla completa perdita
di energia degli spin che viene trasferita all’ambiente sotto forma di calore, sebbene le energie
coinvolte sono così piccole che le variazioni di temperatura non sono rilevabili.
Sperimentalmente si osserva che la magnetizzazione lungo z torna alle condizioni di equilibrio
seguendo un andamento esponenziale:
M z = M z0 (1 − e −t / T1 )
(ton = 0)
(3.8)
dove M0z è la magnetizzazione all’equilibrio termico, T1 è la costante di tempo per questo processo
e viene chiamata tempo di rilassamento longitudinale.
Dopo l’impulso gli spin possiedono coerenza di fase quindi la magnetizzazione totale nel piano
trasversale risulta essere diversa da zero. Se gli spin fossero uguali questi dovrebbero rimanere
statici nel sistema di assi rotanti e nel caso di un impulso di π/2 perfettamente allineati lungo l’asse
y. Questo avviene nel caso il campo magnetico agisca su ogni spin del campione con la stessa
forza. In realtà alcuni spin subiranno un campo magnetico locale leggermente più forte rispetto alla
media, avranno quindi una frequenza più alta e ruoteranno attorno all’asse z più velocemente,
mentre altri subiranno un campo magnetico locale meno intenso rispetto alla media e ruoteranno più
lentamente. Questo porta a una perdita di coerenza di fase degli spin e il modulo della
magnetizzazione trasversale di conseguenza diminuirà fino a diventare uguale a zero quando sono
ripristinate le condizioni di equilibrio.
tempo
y
x
y
y
y
x
x
Figura 3.8
48
x
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Questa è un’altra forma di rilassamento che viene definita come rilassamento trasversale e ha un
andamento a decadimento esponenziale:
M x , y = M x0, y (e −t / T2 )
(toff = 0)
(3.9)
dove M0x,y è la magnetizzazione all’equilibrio termico, T2 è la costante di tempo di questo processo,
chiamata tempo di rilassamento trasversale.
Dopo l’applicazione del campo a radiofrequenze la componente perpendicolare a z continuerà a
ruotare alla frequenza di risonanza con una traiettoria a spirale smorzata determinata dai due
meccanismi di rilassamento longitudinale e trasversale (Figura 3.9a):
(a)
(b)
(c)
FID
Figure 3.9
49
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
permettendo di ottenere un segnale di risposta mediante induzione di un segnale elettrico nella
bobina del circuito di rivelazione (disposta con l’asse perpendicolare al campo statico B0 e
solitamente coincidente con il circuito di trasmissione dell’impulso a RF) (Figura 3.9b).
Il segnale indotto, il decadimento libero dell’induzione (free induction decay, FID), risulta essere
un segnale oscillante nel tempo alla frequenza di risonanza e per effetto delle interazioni del sistema
di spin con l’ambiente decade nel tempo (Figura 3.9b). Il FID corrisponde quindi ad un’oscillazione
smorzata. La durata del segnale dipende dal tempo di rilassamento trasversale (T2) (Figura 3.9c),
ma l'interferenza tra i nuclei che risuonano a frequenze differenti causa uno smorzamento più
veloce. Tuttavia, in soluzione, il decadimento libero dell'induzione è limitato dal rilassamento e il
segnale è approssimativamente esponenziale con una costante T2. Le componenti lungo gli assi x e
y della magnetizzazione in funzione del tempo sono espresse dalle relazione:
M x = M z0 sen(ωt )e −t / T2
M y = − M z0 cos(ωt )e −t / T2
Lo spettro corrispondente nel dominio delle frequenze viene ottenuto tramite la trasformata di
Fourier:
F (ν ) ∝
T2
2
1 + 4π (ν −ν L ) 2 T2
2
(3.10)
FT
Dominio del tempo
Dominio delle frequenze
Frequenza
Tempo t
Figura 3.10
ed è dato da una o più righe caratterizzate da una forma lorentziana, la cui larghezza ∆ν1/2 è
inversamente proporzionale al tempo T2.
Chemical shift e accoppiamento scalare
50
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Uno spettro protonico si presenta come una serie di picchi che a seconda del loro numero, posizione
e area permettono di ricavare numerose informazioni sulla struttura della molecola.
La posizione dei picchi, detta spostamento chimico (chemical shift), viene misurata in unità di
frequenza rispetto a un picco di riferimento secondo la seguente relazione:
δ = 10 6
ν −ν rif
ν rif
ppm
(3.11)
dove ν è la frequenza di risonanza della linea considerata e νrif è la frequenza di risonanza di un
composto di riferimento che in genere è il tetrametilsilano (TMS), un composto chimicamente
inerte, simmetrico, volatile, e solubile nella maggior parte dei solventi organici. Le frequenze di
risonanza osservate per i protoni di una molecola sono diversi dai valori ottenuti usando la relazione
3.6 in quanto il campo magnetico B0 induce una circolazione nella nube elettronica che circonda il
protone e quindi in base al principio di Lenz è prodotto un momento magnetico che si oppone a B0.
Il campo magnetico locale risulterà di conseguenza più piccolo di B0. Questo effetto corrisponde a
uno schermo magnetico sul protone che riduce B0 di un ammontare pari a σ B0, dove σ è conosciuta
come costante di schermo:
Blocale = B0(1-σ)
(3.12)
Di conseguenza protoni con intorno chimico diverso avranno frequenze di risonanza diverse in
quanto saranno affetti da campi magnetici locali di intensità diversa. Inoltre ciascun segnale può
presentare un certo numero di linee (splitting). La causa di questa “struttura fine” è l’accoppiamento
spin-spin (J) ed è dovuto all’interazione magnetica tra protoni che non è trasmessa attraverso lo
spazio ma dagli elettroni di legame tramite i quali i protoni sono indirettamente connessi.
Generalmente l’accoppiamento perde importanza oltre il terzo legame, a meno non sia presente una
tensione d’anello (sistemi ciclici piccoli), una delocalizzazione (sistemi aromatici o coniugati), o
una sistema di quattro legami successivi disposti a W. I profili di splitting semplici prodotti
dall’accoppiamento di protoni che possiedono chemical shift molto diversi (∆ν/J ≥ 10), sono
chiamati spettri di primo ordine e possono venire interpretati seguendo due semplici regole:
1. La molteplicità è pari a (n + 1) , dove n è il numero dei protoni vicini equivalenti.
2. Le intensità relative dei picchi di un multipletto dipendono da n secondo la formula generale
(a + b)n; quando il binomio viene sviluppato per il valore desiderato di n i coefficienti
51
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
forniscono le intensità relative. La molteplicità e le intensità relative possono essere facilmente
ricavate dal triangolo di Pascal in cui n è il numero di protoni accoppiati:
1
1
1
1
1
1
2
3
4
1
3
6
1
4
1
Schema 3.1
L’area dei picchi è proporzionale al numero di protoni che rappresentano.
52
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Esperienza 3. NMR dinamico
Obiettivo: Determinare la dinamica dell’equilibrio e l’energia di attivazione del seguente processo
della N,N-dimetilformammide (DMF) mediante la registrazione di una serie di spettri protonici a
varie temperature.
a'
N
H3C
a
a
O
H3C
O
H3C
C
N
C
H3C
H
a'
H
Schema 3.2
In numerose situazioni lo spettro NMR non può essere interpretato soltanto sulla base del chemical
shift e delle costanti di accoppiamento, ma è necessario considerare anche l’effetto che i moti
all’interno della molecola producono sulla forma delle righe spettrali.
Quando i moti coinvolgono scambi tra intorni molecolari diversi si parla, convenzionalmente,
di NMR dinamico (DNMR). Per capire come la tecnica DNMR possa essere sfruttata per avere
informazioni sulle velocità coinvolte nei processi cinetici di scambio, consideriamo un caso molto
semplice che, tuttavia, si incontra frequentemente nelle misure sperimentali.
Consideriamo due nuclei (o insiemi di nuclei equivalenti) (A) e (B) non accoppiati nè tra loro nè
con altri nuclei. Questi nuclei possono occupare due diversi intorni chimici nella molecola. E
consideriamo il caso semplice in cui le due situazioni abbiano la stessa energia e quindi la stessa
probabilità di verificarsi. Inoltre supponiamo che il nucleo A scambi con il nucleo B con una
velocità indipendente dalla concentrazione, ovvero che la costante cinetica k1, in condizioni di
equilibrio, sia del primo ordine ed uguale alla costante inversa k-1.
k-1
(A)
(B)
k-1
Schema 3.3
La misura della costante di velocità di una reazione veloce e reversibile e la determinazione delle
rispettive entalpie e entropie di attivazione possono venire studiate mediante spettroscopia NMR, in
quanto la forma della linea dei segnali NMR è sensibile ai processi di scambio chimico se questi
influenzano i parametri NMR dei nuclei. Gli spettri NMR di molti composti sono quindi dipendenti
dalla temperatura. Alla frequenza del protone, A e B rappresentano l’insieme dei tre identici protoni
53
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
metilici. Questi tre protoni possono essere trattati come se fossero soltanto due nuclei come i due
atomi di carbonio. La sola differenza sarà l’intensità del segnale che sarà tre volte maggiore rispetto
al caso di due nuclei singoli di idrogeno. Nella conformazione planare a più bassa energia della
molecola di DMF i protoni dei due gruppi metilici si trovano in differenti intorni chimici e quindi
hanno diverse frequenze di risonanza νA e νB (figura 3.11a).
340K
(a)
(b)
385K
389K
390K
391K
(c)
392K
395K
(d)
3.10
3.00
2.90
2.80
2.70
2.60
2.50
2.40
Figura 3.11
Al variare della temperatura varierà la velocità di rotazione e sarà maggiore ad alta temperatura.
A temperatura ambiente l’andamento dello spettro è rappresentato in Figura 3.11a: i due segnali
metilici sono separati tra loro da 16 Hz (cioè 16 s-1). Questa situazione viene definita,
impropriamente, come “assenza di scambio”. In realtà questo non significa che la rotazione non
avvenga ma che il processo è così lento (k1 ≤ ∆ν0 = νA − νB) nella scala dei tempi NMR (meno di
una o due rotazioni ogni secondo) da risultare “invisibile”. La rotazione interna attorno al legame
N-CO porta a uno scambio intramolecolare dei gruppi metilici, ma a causa dell’alta barriera di
energia la frequenza di scambio a temperatura ambiente è bassa. Il tempo di residenza dei gruppi
metilici in posizioni cis e trans rispetto al gruppo carbonilico sono relativamente lunghi e quindi si
osservano due segnali di risonanza separati la cui larghezza a mezza altezza (tipicamente 0.5 Hz)
54
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
dipende essenzialmente dall’omogeneità del campo magnetico.
A temperatura maggiore questi segnali si allargano (Figura 3.11b) e la costante k1 è maggiore ma
comunque inferiore a (νA − νB) (16 Hz). Questo significa che avvengono meno di 16 rotazioni al
secondo. L’ampiezza di riga è ora maggiore della risoluzione ω0 ma i due segnali sono ancora
separati e la sovrapposizione è piccola. In queste condizioni il valore della costante è dato da
k1 = π(ω − ω0)
(3.13)
dove ω è l’ampiezza di riga sperimentale e ω0 l’ampiezza di riga in assenza di scambio.
Quando la temperatura cresce ulteriormente il valore di k1 aumenta, i segnali si sovrappongono e la
relazione (3.13) non può essere usata. In queste condizioni, quindi, la posizione del massimo della
riga allargata non corrisponde più esattamente al chemical shift. Questo fenomeno distingue il
processo di scambio da quello di una semplice sovrapposizione di due righe che abbiano
un’ampiezza di riga elevata. In queste condizioni la costante risulta espressa da:
k1 = π2−1/2(∆ν0 2 − ∆ν 2)1/2
(3.14)
dove ∆ν0 è la differenza tra gli shift (νA − νB) in assenza di scambio e ∆ν è la differenza misurata
in questa situazione.
Alla temperatura detta di coalescenza Tc lo spettro si presenta come una sola riga di forma
trapezoidale, con un massimo molto appiattito. In queste condizioni la costante k1 può essere
ricavata dalla relazione
k1 = π2−1/2 (νA − νB ) = 2.22 (νA − νB)
(3.15)
Nelle nostre condizioni questo si verifica tra a 390-392 K (figura 3.11c) e poiché la differenza di
shift (νA − νB ) è 16 Hz, k1 risulta uguale a ca. 36 s-1.
A Tc il segnale collassa e diventa unico e allargato e la sua posizione è la media dei due chemical
shift (figura 3.11d). A temperatura molto più alta (non indicata in figura) la riga unica è diventata
stretta e la sua larghezza è in pratica indipendente dalla velocità di scambio tornando a dipendere
dai normali parametri che regolano la larghezza di riga in sistemi statici.
Apparentemente ad alte temperature lo strumento non è più in grado di differenziare tra gruppi
metilici cis e trans. Questo effetto dipende dalla bassa differenza di energia esistente tra due siti
magnetici a diversa frequenza di Larmor, la cui misura dipende dal tempo di vita, τ, dei nuclei in
55
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
ogni sito che deve essere sufficientemente lungo. In accordo al principio di incertezza il più basso
limite di τ è data da
τδν ≈ 1/2π
(3.16)
dove δν = ∆E/h è la differenza tra le frequenze νA − νB coinvolte. Se τ diventa troppo piccolo, si
osserva uno spettro mediato nel tempo. Nel caso della dimetilformammide ad alta temperatura la
frequenza della rotazione interna diventa elevata provocando quindi una diminuzione del tempo di
vita dei protoni metilici nelle posizioni a differente frequenza di Larmor e un solo segnale è
osservato.
Per stabilire la correlazione tra la forma della linea dello spettro NMR e il meccanismo e la cinetica
dei processi dinamici si deve trovare una correlazione tra il tempo di vita dei protoni in posizione A
e B e la forma della linea del segnale NMR, questo è possibile utilizzando le equazioni di Bloch che
descrivono la forma del segnale di risonanza come funzione della frequenza ν e il tempo di
rilassamento trasversale T2.
Attraverso l’equazione di Eyring è quindi possibile valutare l’energia di attivazione alla temperatura
Tc che dopo le adeguate sostituzioni risulta:
∆G‡ = RTc [22.96 + ln(Tc/δν)] (J mol-1)
(3.17)
A temperatura maggiore di Tc e quando ω > ω0 l'espressione della costante cinetica è data da
k1 = π 2 −1/2
(∆ν 0 )2
ω − ω0
(3.18)
L’ordine di grandezza delle costanti di velocità che possono essere determinate mediante la
spettroscopia NMR dipende dalla frequenza a cui opera lo strumento ed è compreso tra 1 e 105 s-1 in
processi dinamici caratterizzati da barriere di energia tra 20 e 100 kJmol-1 (5 e 25 kcal mol-1).
56
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Caratteristiche dello strumento
Le parti principali di uno spettrometro NMR sono:
 Un campo magnetico intenso, stabile ed omogeneo di circa 4.7 Tesla corrispondente alla
frequenza di risonanza del protone di 200 MHz, generato da un magnete superconduttore, che
consiste in una spira di lega di Nb attraverso la quale passa corrente elettrica immersa in un
bagno di elio liquido contenuto in un dewar, posto all’interno di un secondo dewar riempito di
azoto liquido che serve per ridurre l’evaporazione dell’elio liquido. L’intero apparato è
circondato da un’intercapedine, dove viene fatto il vuoto. Al centro del dewar del magnete vi è
un foro che si trova a temperatura ambiente dove sono collocate una serie di bobine chiamate
shim coils che generano piccoli campi magnetici con particolari profili spaziali e permettono di
stabilizzare il campo magnetico principale e rimuovere disomogeneità residue. La corrente
all’interno di queste bobine viene aggiustata finché il campo magnetico ha l’omogeneità
richiesta, cosa che può venire valutata facilmente registrando lo spettro di un campione che ha
come segnale di risonanza una linea stretta. I moderni spettrometri possono avere fino a 40
diverse shim coils, i cui nomi corrispondono al profilo di campo che generano.
 Un “probe”. È un tubo metallico cilindrico posto al centro del magnete contenente una bobina di
radiofrequenza per eccitare e ricevere la radiazione elettromagnetica, una termocoppia e una
resistenza per riscaldare il campione. Il campione che si trova in un tubo cilindrico di vetro è
tenuto da uno spinner e scende nel probe attraverso una colonna di aria. I probe possono avere
varie dimensioni di diametro e lunghezza, a seconda delle caratteristiche di costruzione del
magnete, solitamente vengono definiti in base al diametro dei tubi che possono contenere. I più
usati sono quelli di diametro 5 mm. I probe possono venire dedicati all’osservazione di un una
singola frequenza (probes selettivi), di un ampio intervallo di frequenze (broadband probes) o
di predefiniti intervalli di frequenze (per esempio per quattro nuclei diversi, quad-nucleus
probes). In tutti i casi sono in grado di osservare simultaneamente la frequenza del deuterio per
fornire un segnale per la regolazione del campo (lock signal). In genere è incorporato una
seconda bobina per permettere la simultanea applicazione di impulsi su uno o più nuclei e in
alcuni casi vi sono altre bobine che vengono utilizzate per distruggere il campo magnetico in
modo controllato (field gradient coils).
 Un trasmettitore di radiofrequenze (RF) ad alta potenza capace di generare e trasmettere corti
impulsi. Come sorgente di RF viene usato un sintetizzatore di frequenze controllato da PC che
genera frequenze stabili che possono venire fissate precisamente.
 Un ricevitore che amplifica i segnali NMR.
57
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
 Un digitalizzatore per convertire i segnali NMR in una forma che può essere immagazzinata
dalla memoria del computer.
 Un programmatore di impulsi per produrre impulsi di precisa durata.
 Un computer per controllare ogni cosa e processare i dati.
58
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
CALIBRAZIONE
VARIABLE TEMPERATURE UNIT (VTU)
Campione: 80% 1,2-etandiolo in [D6]DMSO
T [K] = -108.33 ∆δ + 460.41
300K
310K
320K
330K
340K
350K
360K
370K
380K
390K
400K
5,5
5,0
4,5
4,0
δ (ppm)
59
3,5
3,0
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Temperatura nominale [K] δ (OH) [ppm]
300
310
320
330
340
350
360
370
380
390
400
δ (CH2) [ppm]
∆δ [ppm]
Temperatura reale [K]
3.49
3.49
3.49
3.49
3.49
3.49
3.49
3.49
3.49
3.49
3.49
1.48
1.37
1.26
1.15
1.04
0.94
0.83
0.72
0.61
0.52
0.40
300.1
312.0
323.9
335.8
347.7
359.1
370.8
382.5
394.0
404.2
416.6
4.97
4.86
4.75
4.64
4.53
4.42
4.32
4.21
4.10
4.00
3.89
T reale = -(47.9 ± 1.9) + (1.162 ± 0.005) x T nominale
deviazione standard = 0.6
60
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Norme generali di sicurezza
Le apparecchiature NMR a causa dei campi magnetici associati possono presentare numerosi
pericoli. È necessario quindi prendere alcune precauzioni per assicurarsi che questi rischi siano
ridotti il più possibile. Alcuni effetti sono di seguito elencati:
•
Forze attrattive molto potenti possono venire esercitate su oggetti ferromagnetici come attrezzi,
chiavi, bombole di gas, estintori che si trovino in prossimità del sistema magnetico. Queste
forze possono diventare abbastanza elevate da muovere in modo incontrollato gli oggetti verso
il magnete e i pezzi più piccoli possono diventare dei proiettili, nel migliore dei casi occorrerà
tempo e fatica per riuscire ad allontanarli ma non sono improbabili eventi peggiori quali:
•

Quenching

Perdita di vuoto nel magnete

Rottura dell'involucro esterno

Urto con oggetti volanti

Asfissia a seguito di improvviso quenching (evaporazione di He e N2 liquidi)
Impianti medici elettronici, elettrici e meccanici come pacemakers cardiaci, biostimolatori e
neurostimolatori possono operare in modo improprio o essere fermati in presenza di campi
magnetici. Persone con tali impianti non dovrebbero entrare nel laboratorio NMR (considerare
la possibilità che il campo dei 5 gauss possa estendersi anche fuori del locale che ospita il
magnete).
•
Impianti chirurgici possono contenere materiali ferromagnetici e quindi possono essere soggetti
a elevate forze attrattive in vicinanza di magneti. Questo può provocare danni gravi o morte.
Inoltre in vicinanza di campi magnetici che cambiano velocemente possono venire indotte delle
correnti nell’impianto e queste generare un riscaldamento. A persone con protesi metalliche
(comprese quelle dentali) è fatto divieto di oltrepassare per qualsiasi ragione la linea dei 5
Gauss.
•
Oggetti come orologi, registratori, macchine fotografiche possono essere magnetizzati e
irreparabilmente danneggiati se sottoposti a campi magnetici superiori a 10 Gauss.
•
Carte di credito, carte telefoniche, supporti non magnetici di ogni genere non costituiscono di
per sé pericolo ma possono essere rovinati se avvicinati a forti campi magnetici. Orologi digitali
non dovrebbero in linea di massima essere influenzati dal campo, ma in dubium abstine. Gli
61
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
orologi tradizionali possono subire danni e renderne necessaria la smagnetizzazione. Possono
comunque in certi casi subire danni irreversibili.
Le seguenti regole devono essere applicate dagli utenti NMR:
•
Persone con impianti cardiaci o medici non devono entrare nell’area all’interno dei 5 Gauss.
•
Tutti gli oggetti magnetici devono essere tenuti all'esterno della linea dei 5 Gauss.
Considerare ogni oggetto come magnetico fino a che non si è dimostrato il contrario.
Sono sicuramente da considerare magnetici e quindi potenzialmente pericolosi:
 CHIAVI
 ATTREZZI
 COLTELLI
 BOMBOLE DI GAS COMPRESSO
 CONTENITORI PER LIQUIDI REFRIGERANTI
 ESTINTORI
Nel caso che un oggetto venga attratto dal magnete NON cercate di liberarlo ma avvisare
immediatamente l'incaricato.
•
Mantenere gli strumenti elettronici all'esterno della linea sopra indicata.
•
Utilizzare solamente attrezzi non magnetici all'interno della linea sopra indicata.
•
In dubio abstine. Non avvicinarsi al magnete se non per ragioni di servizio. La
strumentazione è estremamente costosa.
•
Nessun estraneo deve entrare nei locali se non accompagnato da un responsabile che li
informi delle misure di sicurezza.
•
Solo coloro che hanno preso visione delle misure di sicurezza dovrebbero essere presenti nel
Laboratorio di NMR e sono autorizzate a superare la linea dei 5 gauss. Devono comunque
assicurarsi di aver depositato oggetti personali suscettibili di danno in un luogo sicuro prima
di avvicinarsi al magnete.
La zona di esclusione che comprende l’area all’interno della linea dei 5 gauss viene definita in
modo chiaro.
62
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Principali comandi.
Inserimento campione
1) Introdurre il tubo NMR nello spinner per alte temperature
2) Misurare la profondità con l’apposito strumento, la base deve essere allo stesso livello della
scritta 5mm
3) Togliere il tappo dalla testa del magnete
4) Premere il pulsante arancio second e poi lift
5) Introdurre il tubo nel probe
6) Premere lift off
7) Riporre il tappo alla testa del magnete
Shimatura
1) Premere field e centrare la sweep
2) Premere lock
3) Quando il pulsante del lock non lampeggia più premere spin
4) Migliorare l’omogeneità agendo in modo interattivo sulle shim z, z2 e z3
Comandi di acquisizione
1) Digitare O1 (Trasmitter Offset Frequency) e impostare 3585Hz (valore per C2D2Cl4)
2) Digitare SW (Spectral Width) e impostare 2400 (Hz)
3) Digitare TD (Time Domain Size) e impostare 16K
4) Digitare SI (Size of Allocated Memory) e impostare 32K
5) Digitare PW (Pulse Width) e verificare che il valore impostato sia 6.30 (µs)
6) Digitare RD (Relaxation Delay) e impostare 2 (s)
7) Digitare NS (Number of Scans) e impostare 8
8) Digitare GS (Go-Setup mode) e controllare che il segnale del FID sia contenuto all’interno dei
primi due quadretti, agendo su RG (Receiver Gain) si riporta il segnale all’interno dei primi due
quadretti
9) Digitare ctrl H per stoppare l’acquisizione
10) Digitare ZG (Ze and Go) per iniziare ad acquisire lo spettro
11) Finita l’acquisizione digitare WR + nome (Write Data File, max 8 caratteri più 3 caratteri per
estensione) per salvare il FID.
12) Digitare FT (Fourier Transformation) per trasformare lo spettro nel dominio delle frequenze
63
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Comandi di processamento
Digitando EP (Interactive Display and Expansion of 1D Data) si entra nella finestra dove è
possibile elaborare lo spettro.
1) Correzione di fase
Per questa operazione si utilizzano le quattro manopole in alto a sinistra.
A: permette di spostare lo spettro da destra a sinistra
B: permette di allargare e stringere lo spettro
C: fa muovere il cursore velocemente verso destra o sinistra
D: fa muovere il cursore lentamente verso destra o sinistra
Vertical Display: aumenta (+) o diminuisce (-) l’intensità dello spettro
Portarsi sul picco più intenso digitare P correggere con la manopola C, controllare il resto dello
spettro con la manopola A e eventualmente correggere la fase con la manopola D. Memorizzare
la fase con M. Se con le manopole C e D si arriva a fine corsa digitare rispettivamente Ctrl/C e
Ctrl/D
2) Calibrazione Spettro
Portare il cursore con la manopola C e poi con quella D sul picco del composto di riferimento
(TMS) digitare G e impostare 0 seguito da RETURN.
3) Sovrapposizione Spettri
Digitando D (Dual Display Routine) compare la scritta TOP TRACE FILE NAME quindi se lo
spettro da sovrapporre si trova nel job 2 digitare SPC2, se è invece nel job 3 digitare SPC3.
Sullo schermo compaiono due spettri: quello che si sta eleborando (primo spettro) in verde e
quello che si vuole sovrapporre in rosso (secondo spettro).
I tasti I (Increase) e D (Decrease) permettono rispettivamente di avvicinare e allontanare i due
spettri;
Vertical Display: aumenta (+) o diminuisce (-) l’intensità di entrambi gli spettri;
La manopola A permette di spostare entrambi gli spettri da destra a sinistra;
La manopola B permette di allargare e stringere entrambi gli spettri;
La manopola C permette di spostare il primo spettro da destra a sinistra;
La manopola D permette di aumentare o diminuire l’intensità del primo spettro;
Per ritornare a visualizzare un unico spettro digitare RETURN.
64
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
Procedura sperimentale
Non sovrariscaldare il campione
Non superare la temperatura di 400K!
Apparecchiatura: spettrometro NMR operante a 200MHz, tubo per misure NMR, spinner per
misure ad alte temperature, 1 siringa da 50 µl, 1 siringa da 1 ml.
Reagenti: N,N-dimetilformammide, 1,1,2,2,-tetracloroetano-d2.
Primo pomeriggio
In un tubo NMR vengono introdotti 25 µl di N,N-dimetilformammide, 0.5 ml di 1,1,2,2,tetracloroetano-d2, e vapori di TMS.
Al controllo di temperatura si imposta 320K si lascia equilibrare il campione per almeno 5 minuti,
si registra lo spettro protonico del campione. Si registrano i relativi spettri 1H a diverse temperature,
variando per incrementi di 20 K all’inizio e di 2 K vicino alla temperatura di coalescenza.
Secondo pomeriggio
Gli spettri vengono trasferiti al PC, processati e stampati sia interi sia espandendo la zona dei gruppi
metilici. Si riporta inoltre in una singola stampa tutte le misure indicando le varie temperature.
Si determinano le costanti di velocità alle varie temperature utilizzando le opportune equazioni:
quando l’ampiezza di riga è ora maggiore della risoluzione ω0 ma i due segnali sono ancora separati
e la sovrapposizione è piccola
k1 = π(ω − ω0)
(3.13)
dove ω è l’ampiezza di riga sperimentale e ω0 l’ampiezza di riga in assenza di scambio;
quando i massimi si avvicinano e quindi la posizione del massimo della riga allargata non
corrisponde più esattamente al chemical shift:
k1 = π2−1/2(∆ν0 2 − ∆ν 2)1/2
(3.14)
dove ∆ν0 è la differenza tra gli shift (νA − νB) in assenza di scambio e ∆ν è la differenza misurata
in questa situazione;
65
Laboratorio di Chimica Fisica
NMR
Annalisa Bisello, Saverio Santi
alla temperatura di coalescenza Tc e lo spettro si presenta come una sola riga di forma trapezoidale,
con un massimo molto appiattito:
k1 = π2−1/2 (νA − νB ) = 2.22 (νA − νB)
(3.15)
a temperatura maggiore di Tc e quando ω > ω0
k1 = π 2 −1/2
(∆ν 0 )2
ω − ω0
(3.18)
N.B. I valori di temperatura nominale devono essere convertiti nei valori di temperatura reale
utilizzando l’equazione della retta di taratura.
Con i valori di k ottenuti ad ogni temperatura calcolare ∆G≠ (a Tc), ∆H≠ e ∆S≠ dall’equazione di
Eyring (esperienza 2) nella forma:
d ln k 1 d ln K ≠
= +
dT
T
dT
Per confronto, utilizzando la temperatura di coalescenza, il valore δν dei gruppi metilici nella zona
di scambio lento, si calcola la costante di velocità e l’energia di attivazione ∆G≠ attraverso le
relazioni 3.15 e 3.17
k1 = π2−1/2 (νA − νB ) = 2.22 (νA − νB)
(3.15)
∆G≠ = RTc [22.96 + ln(Tc/δν)] (J mol-1)
(3.17)
I dati vanno presentati in opportuna tabella e commentati.
66