Ingegneria dei Sistemi Elettrici_5b
La legge di Biot-Savart e applicazioni
In molte applicazioni è richiesta la determinazione del campo
magnetico dovuto a un circuito attraversato dalla corrente.
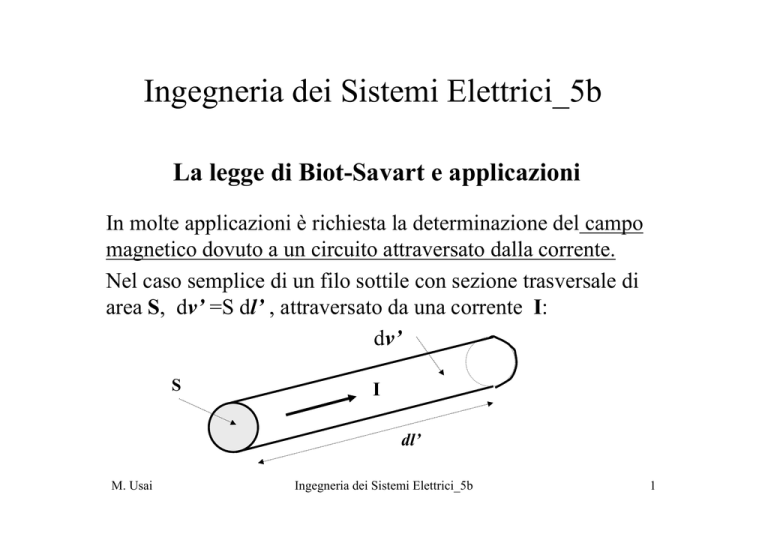
Nel caso semplice di un filo sottile con sezione trasversale di
area S, dv’ =S dl’ , attraversato da una corrente I:
dv’
S
I
dl’
M. Usai
Ingegneria dei Sistemi Elettrici_5b
1
si ha:
[ ]
⎡ A⎤
J dv' = ( JS )dl' = I dl' con J ⎢ 2 ⎥ e dv' = Sdl ' m 2
⎣m ⎦
µo
e l’espressione del potenziale A =
4π
J
∫V' R dv'
⎡Wb ⎤
⎢⎣ m ⎥⎦
diventa:
µ0 I d l' ⎡Wb ⎤
4π C'∫ R ⎢⎣ m ⎥⎦
dove il simbolo di integrale circolare indica che la corrente fluisce
in un circuito chiuso che é indicato con C’.
La densità di flusso magnetico é dunque:
A=
⎡ µ o I d l' ⎤ µ o I
⎛ dl' ⎞
B = ∇× A = ∇× ⎢
=
∇×⎜ ⎟
⎥
∫
∫
⎝R⎠
⎣ 4π C' R ⎦ 4π C'
M. Usai
Ingegneria dei Sistemi Elettrici_5b
2
E’ molto importante notare che l’operatore rotore comporta il
calcolo delle derivate rispetto alle coordinate spaziali del punto
del campo, e che l’operatore integrale é fatto rispetto alle
coordinate della sorgente. L’integrando può essere espanso in
due termini usando la seguente identità:
∇ × ( f G ) = f ∇ × G + (∇ f )× G
Si ha per f = 1/R e G = dl’;
µo I ⎡ 1
⎤
⎛ 1⎞
∇
×
+
∇
×
B=
d
l'
d
l
'
⎜
⎟
⎥⎦
4π C'∫ ⎢⎣ R
R
⎝
⎠
ora poiché le coordinate utilizzate per il calcolo del rotore e
quelle usate per il calcolo dell’integrale sono indipendenti,
∇× d l' é uguale a zero e il primo termine del secondo membro si
annulla.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
3
La distanza R é misurata da dl’, a partire da (x’,y’,z’) sino al punto
del campo (x,y,z). Quindi si ha:
[
1
2
2
2
= ( x − x' ) + ( y − y' ) + ( z − z' )
R
]
1
2
∂ ⎛1⎞
∂ ⎛1⎞
∂ ⎛1⎞
⎛1⎞
∇ ⎜ ⎟ = ax ⎜ ⎟ + a y ⎜ ⎟ + az ⎜ ⎟ =
∂x ⎝ R ⎠
∂y ⎝ R ⎠
∂z ⎝ R ⎠
⎝ R⎠
=−
a x ( x − x' ) + a y ( y − y' ) + a z ( z − z' )
[( x − x' )
2
+ ( y − y' ) + ( z − z' )
2
]
3
2 2
=−
R
1
=
−
a
R
3
R
R2
[T]
dove a R é il vettore unitario diretto dal punto sorgente al punto
del campo.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
4
Sostituendo nella espressione precedente di B si ottiene:
µo I
⎛ dl ' ⎞
B = ∇× A =
∇×⎜ ⎟ ⇒
4π
R⎠
⎝
C'
∫
µo I d l' × a R
B=
4π C'∫ R 2
[T ]
questa relazione é nota come equazione di Biot-Savart.
La formula della legge di Biot-Savart, consente di determinare B
dovuta alla corrente I concatenata dal percorso chiuso C’ ed è stata
ottenuta calcolando il rotore della espressione potenziale vettore A :
A=
M. Usai
µ0 I d l'
4π C'∫ R
⎡Wb ⎤
⎢⎣ m ⎥⎦
Ingegneria dei Sistemi Elettrici_5b
5
I alcuni casi é conveniente scrivere l’equazione in due passi
successivi:
B = ∫dB
[T ]
C'
µo I ⎛ d l' × a R ⎞
dB =
⎟
⎜
2
4π ⎝ R
⎠
[T ]
d B é la densità di flusso magnetico dovuta alla corrente
elementare I dl’.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
6
Una forma alternativa della legge di Biot-Savart , talvolta più
conveniente é:
µ o I ⎛ d l' × R ⎞
dB =
⎜
⎟
3
4π ⎝ R ⎠
[T]
Confrontando l’espressione di B con l’espressione della legge
della circuitazione di Ampere, si vede come la legge di BiotSavart sia più difficile da applicare.
Anche se la legge della circuitazione di Ampere é utilizzabile
per determinare B , nota la corrente I nel circuito solo se può
essere definito un percorso chiuso lungo il quale B ha
ampiezza costante.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
7
Dipolo magnetico
x
Per determinare il momento di un dipolo magnetico si determina
la densità del flusso magnetico B in un punto posto ad una certa
distanza da una spira circolare elementare di raggio b, attraversata
dalla corrente I, che costituisce un dipolo magnetico.
Si vuole determinare B in P
P(R,θ;π/2)
z
la cui distanza R dal centro della
R
spira soddisfi la relazione R>>b,
θ
(ciò comporta semplificazioni).
R1
I
Si sceglie inoltre il centro della
b
Ψ
spira come origine delle
φ’
coordinate sferiche:
y
d l' = (− a x sin φ' + a y cos φ' ) b dφ'
P’ dl’
M. Usai
Ingegneria dei Sistemi Elettrici_5b
8
Si determina da prima A e quindi B = ∇ × A , dalla relazione:
µ0 I d l'
A=
4π C'∫ R1
⎡Wb ⎤
⎢⎣ m ⎥⎦
dove R1 indica la distanza tra la sorgente elementare dl’ in P’ e il
punto P .
µ 0 Ib 2
Si dimostra che: A = a φ 4 R 2 sinθ e dalla relazione: B = ∇ × A
si ottiene:
µ 0 Ib 2
(a R 2 cosθ + aφ sinθ )
B=
3
4R
simile alla espressione del campo elettrico per un dipolo elettrico:
p
(a R 2 cosθ + aφ sinθ )
E=
3
4πε 0 R
M. Usai
Ingegneria dei Sistemi Elettrici_5b
9
Si noti come
• nei punti distanti dai dipoli elettrico e magnetico: le linee di flusso
magnetico sono le stesse per il campo elettrico e magnetico rispettivamente,
mentre
• in prossimità dei dipoli: le linee di flusso del dipolo magnetico sono
continue, mentre le linee di flusso del dipolo elettrico terminano sulle
cariche, partendo dalla carica positiva verso la carica negativa.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
10
[
m = a z Iπ b 2 = a z IS = a z m A ⋅ m 2
]
A=
µ0 m × a R
4πR
2
[Wb / m]
Quindi per i punti P la cui distanza dal centro della spira R>>b
B=
µ0m
4π R
3
(a R 2cosθ + a φ
sinθ )
[T ]
L’espressione della densità di flusso magnetico B appare così
ancora più simile alla espressione del campo elettrico E per un
dipolo elettrico:
E=
M. Usai
p
4πε 0 R
(a R 2 cos θ + aφ sin θ )
3
Ingegneria dei Sistemi Elettrici_5b
⎡V⎤
⎢⎣ s ⎥⎦
11
Potenziale magnetico scalare
In una regione dello spazio priva da correnti J = 0 l’equazione:
∇ × B = µo J
diventa: ∇ × B = 0 per cui la densità di flusso magnetico B è
irrotazionale e può essere espressa come il gradiente di un campo
scalare. Si ponga:
B = − µ0 ∇ Vm
dove Vmé chiamato potenziale magnetico scalare (espresso in
ampere).
M. Usai
Ingegneria dei Sistemi Elettrici_5b
12
• Il segno negativo é convenzionale come per l’analoga
definizione del potenziale elettrico scalare:
E = −∇V
• la permeabilità nel vuoto µ0 é semplicemente una costante di
proporzionalità.
In maniera analoga alla equazione della differenza di potenziale
elettrico tra due punti P2 e P1 nel vuoto:
V2 − V1 = −
∫
P2
P1
E ⋅ dl
[V]
possiamo esprimere la differenza di potenziale magnetico scalare
tra due punti P1 e P2 nel vuoto:
P2 1
Vm 2 − Vm1 = −
B ⋅ d l [A]
P1 µ0
∫
M. Usai
Ingegneria dei Sistemi Elettrici_5b
13
Se sono presenti cariche magnetiche con una densità volumica
ρm [A/m2] in un volume V’, il potenziale magnetico Vm si potrà
determinare dalla relazione:
Vm =
1 ρm
dv'
∫
4π V' R
[A]
La densità di flusso magnetico B potrebbe determinarsi dalla
relazione:
B = − µ0 ∇ Vm
M. Usai
Ingegneria dei Sistemi Elettrici_5b
14
Sebbene non siano state mai rilevate sperimentalmente cariche
magnetiche isolate, esse possono essere considerate come cariche
magnetiche fittizie in un modello matematico, non fisico.
Ciò é conveniente:
• sia per la discussione di alcune relazioni magnetostatiche nei
termini delle nostre conoscenze sull’elettrostatica mediante le
analogie,
• che per stabilire un collegamento tra il punto di vista del
tradizionale polo magnetico del magnetismo e il concetto delle
correnti di circolazione microscopiche come sorgenti di
magnetismo.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
15
Il campo magnetico di una piccola barra magnetica è analogo
a quello di un dipolo magnetico.
Ciò può essere verificato sperimentalmente esaminando i
contorni di spire avvolte intorno a un magnete.
L’interpretazione tradizionale è che la posizione delle cariche
magnetiche positive e negative, sia rispettivamente nell’estremità
(polo nord e polo sud) di un magnete permanente.
Per una barretta magnetica si assume che le cariche magnetiche
fittizie +qm e -qm, siano separate da una distanza d e che
formino un dipolo magnetico equivalente al momento:
m = qm d = a n IS
M. Usai
Ingegneria dei Sistemi Elettrici_5b
16
Il potenziale magnetico scalare Vm dovuto a questo dipolo
magnetico si può quindi determinare seguendo una procedura
analoga a quella usata per determinare il potenziale elettrico scalare
dovuto a un dipolo elettrico:
p⋅aR
[V ]
V=
2
4 πε0 R
Analogamente a come é stata ottenuta l’equazione precedente, si
ottiene il potenziale magnetico scalare dovuto a un bipolo
magnetico come:
m ⋅aR
[ A]
Vm =
2
4π R
Sostituendo l’espressione della Vm nella relazione :
B = − µ0 ∇ Vm
M. Usai
Ingegneria dei Sistemi Elettrici_5b
17
Per la densità di flusso magnetico si ottiene la stessa espressione di
ottenibile dal potenziale magnetico vettoriale, data dalla:
B=
µ0m
4πR
3
( a R 2cosθ+a θsinθ )
Si noti che l’espressione del potenziale magnetico scalare Vm per
un dipolo magnetico è esattamente analoga a quella del potenziale
elettrico scalare V per un dipolo elettrico.
L’analogia tra il vettore potenziale magnetico A e il potenziale
elettrico scalare V di un dipolo elettrico, non è però esatta.
Vm =
m ⋅ aR
4π R
M. Usai
2
[A];
A=
µ0 m × a R
4πR 2
⎡ Wb ⎤
⎢⎣ m ⎥⎦ ;
Ingegneria dei Sistemi Elettrici_5b
V=
p ⋅ aR
4πε 0 R
2
[ V ].
18
Si è visto che l’irrotazionalità di B indicata nell’equazione:
∇× B = 0
attraverso la quale si definisce il potenziale magnetico scalare
Vm, è valida soltanto nei punti dove non circolano correnti.
In una regione dove sono presenti correnti, il campo magnetico
non è conservativo, ma ∇ × B = µ o J e il potenziale scalare
magnetico Vm non è una funzione univoca (single-value
function). Quindi la differenza di potenziale magnetico calcolata
in base alla relazione: B = − µ0 ∇ Vm
Vm 2 − Vm 1 = − ∫
P2
P1
1
B⋅dl
µ0
[A]
dipende dal percorso di integrazione.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
19
Per questi motivi, per studiare i campi magnetici nei materiale
magnetici, si userà:
l’approccio della corrente di circolazione I e del potenziale
vettore A ,
al posto
dell’approccio della carica magnetica fittizia qm e del potenziale
scalare Vm.
Si attribuiscono le proprietà macroscopiche di una barretta
magnetica alle correnti atomiche di circolazione (correnti
amperiane) causate da elettroni che orbitano e ruotano su se
stessi (orbiting and spinning).
M. Usai
Ingegneria dei Sistemi Elettrici_5b
20
Magnetizzazione e densità di corrente equivalenti
Secondo il modello elementare atomico della materia, tutti i
materiali sono composti di atomi, ciascuno con un nucleo carico
positivamente e un numero di elettroni carichi negativamente che
orbitano intorno al nucleo.
Gli elettroni che orbitano, causano correnti di circolazione e
formano microscopici dipoli magnetici.
Inoltre, sia gli elettroni che i nuclei di un atomo ruotano intorno
ai loro assi (spin) con determinati momenti di dipolo magnetici.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
21
Il momento di un dipolo magnetico di un nucleo che ruota su se
stesso (spinning) è generalmente trascurabile rispetto a quello di
un elettrone che orbita o ruota su se stesso, perché il nucleo ha una
massa maggiore e una velocità angolare minore.
Per comprendere a pieno gli effetti magnetici dei materiali occorre
conoscere la meccanica quantistica.
• In assenza di un campo magnetico esterno i dipoli magnetici degli
atomi della maggior parte dei materiali, (eccetto i magneti
permanenti) presentano orientazioni casuali, con un momento
magnetico netto risultante nullo.
• L’applicazione di un campo magnetico esterno causa sia
l’allineamento dei momenti magnetici degli elettroni che ruotano
su se stessi e un momento magnetico indotto dovuto alla
variazione del movimento orbitale.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
22
Per ottenere la formula per la determinazione della variazione
quantitativa della densità di flusso magnetico dovuta alla
presenza di materiali magnetici, essendo:
• m k momento del dipolo magnetico di un atomo,
• n
numero di atomi per unità di volume,
si definisce vettore di magnetizzazione M :
n∆ v
M = lim
∆ v →0
∑m
k =1
∆v
k
⎡A⎤
⎢⎣ m ⎥⎦
che è la densità volumica del momento del dipolo magnetico.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
23
Il momento del dipolo magnetico d m di un volume elementare dv’
è: d m = M dv', che in accordo con la relazione:
µ0 m × a R
[Wb / m ]
2
4 πR
da luogo ad un potenziale magnetico vettoriale:
A=
µ0 M × a r
dA=
dv'
2
4π R
⎡ A⎤
⎢⎣ m ⎥⎦
Si dimostra che:
µ0 ∇' × M
µ0 M × a n
A= ∫dA=
dv' +
ds'
∫
∫
V'
4π
R
4π S'
R
V'
dove V’ è il volume del materiale magnetizzato e
a n' è il vettore unitario normale uscente da ds’ e S’ è la superficie
che delimita il volume V’.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
24
Il confronto tra la relazione:
A= ∫dA=
con la relazione:
V'
µ0 ∇' × M
µ0 M × a n
dv'
+
ds'
∫
∫
4π V' R
4π S'
R
µ0 J
⎡Wb ⎤
dv' ⎢ ⎥
A=
∫
4π V' R
⎣m⎦
dove A è espresso in termini di densità volumica di corrente,
suggerisce che:
l’effetto del vettore di magnetizzazione M é equivalente sia una
densità di corrente volumica, che a una densità di corrente
superficiale rispettivamente:
Jm = ∇× M
M. Usai
⎡A⎤
⎢⎣ m 2 ⎥⎦
J ms
⎡A⎤
= M × an ' ⎢ ⎥
⎣m⎦
Ingegneria dei Sistemi Elettrici_5b
25
Quindi la determinazione della densità di flusso magnetico B
dovuto a una assegnata densità di momento del dipolo magnetico M
si riduce alla determinazione delle correnti di magnetizzazione:
⎡A⎤
⎡A⎤
=
×
J
M
a
'
ms
n
⎢⎣ m ⎥⎦
⎢⎣ m 2 ⎥⎦
le cui espressioni sono facilmente derivabili, per poi determinare A
dalla relazione:
Jm = ∇×M
A= ∫dA=
V'
µ0 J m
µ0 J ms
dv'
+
ds'
∫
∫
4π V' R
4π S' R
e quindi ottenere B calcolando il rotore di A :
B = ∇× A
M. Usai
Ingegneria dei Sistemi Elettrici_5b
26
L’equivalenza della densità volumica del momento del dipolo
magnetico con la densità di corrente volumica e la densità di
corrente superficiale può essere qualitativamente spiegata
considerando una sezione di materiale magnetizzato.
M, uscente dal foglio
an
an
Si assume che un campo magnetico
esterno ha causato le correnti di
circolazione. La forza di questo
effetto di magnetizzazione é misurata
con il vettore M .
Sulla superficie del materiale ci sarà
una densità di corrente J ms
J ms = M × a n'
M. Usai
Ingegneria dei Sistemi Elettrici_5b
⎡ A⎤
⎢⎣ m ⎥⎦
27
• Se M é uniforme all’interno del materiale le correnti nei bipoli
atomici adiacenti, che fluiscono in direzioni opposte, si annullano
ovunque producendo delle correnti nette nulle all’interno.
Ciò é insito nella equazione:
⎡ A⎤
Jm = ∇×M ⎢ 2⎥
⎣m ⎦
poiché le derivate spaziali di una costante M sono nulle.
• Se M varia nello spazio, le correnti atomiche interne non si
annullano, dando luogo a una densità di corrente volumica netta J m .
E’ possibile giustificare le relazioni quantitative tra M e le densità
di corrente J m e J ms derivando le correnti atomiche sulla
superficie e all’interno del materiale magnetico.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
28
Densità di carica di magnetizzazione equivalente
Si é visto come in una regione dove non circolano correnti si può
definire un potenziale magnetico scalare Vm, attraverso il quale si
può determinate la densità di flusso magnetico B differenziando,
secondo l’equazione:
B = − µ0 ∇ Vm
In termini di vettore di magnetizzazione M (densità volumica del
momento del dipolo magnetico) si può scrivere:
dVm =
M. Usai
M ⋅aR
4π R2
[ A]
Ingegneria dei Sistemi Elettrici_5b
29
Integrando la relazione precedente:
1
Vm =
4π
∫
V'
M ⋅aR
dv'
2
4π R
si dimostra:
− (∇' ⋅ M )
1 M ⋅ a'n
1
Vm =
ds' +
dv'
∫
∫
4 π S' R
4 π S'
R
dove a n é la normale uscente dall’elemento superficiale ds’ del corpo
magnetico.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
30
Per i campi elettrostatici il potenziale elettrico dovuto a un
dielettrico polarizzato può essere calcolato dalla distribuzione di
cariche superficiali o volumiche:
P ⋅ a'n
− (∇' ⋅ P )
1
1
Vm =
ds' +
dv'
∫
∫
4 πε 0 S' R
4 πε 0 S'
R
con:
⎡C ⎤
⎡C ⎤
ρ ps = P ⋅ a n ⎢ 2 ⎥
e ρ p = −∇ ⋅ P ⎢ 3 ⎥
⎣m ⎦
⎣m ⎦
analogamente un corpo magnetizzato può essere sostituito da una
equivalente (fittizia) densità di carica superficiale di
magnetizzazione ρms e una equivalente densità di carica volumica
di magnetizzazione ρm tale che.
ρms = M ⋅ a n
M. Usai
⎡ A⎤
⎢⎣ m ⎥⎦ e
ρm = −∇ ⋅ M
Ingegneria dei Sistemi Elettrici_5b
⎡ A⎤
2
⎣⎢ m ⎥⎦
31
Intensità del campo magnetico e permeabilità relativa
Poiché l’applicazione di un campo magnetico esterno provoca:
• un allineamento dei momenti dei dipoli interni e
• induce un momento magnetico in un materiale magnetico,
la densità del flusso magnetico risultante in presenza di un
materiale magnetico sarà diversa da quella che il campo genera
nel vuoto.
L’effetto macroscopico della magnetizzazione può essere studiato
incorporando la densità di corrente equivalente volumica Jm
nella equazione rotorica di base valida per il vuoto, ∇ × B = µ o J
ottenendo:
⎛B
⎞
1
∇ × B = J + J m = J + ∇ × M o ∇ × ⎜⎜ − M ⎟⎟ = J
µo
⎝ µo
⎠
M. Usai
Ingegneria dei Sistemi Elettrici_5b
32
Campo elettrostatico
Campo magnetico
n∆ v
n∆
P = lim
∑p
k =1
∆v → 0
V=
1
4πε 0
∆v
k
⎡C ⎤
⎣⎢ m 2 ⎥⎦
P⋅aR
dv' [V ]
2
R
V'
∫
⎡C ⎤
εo E + P = D ⎢ 2 ⎥
⎣m ⎦
M. Usai
M = lim
∆ v →0
dA =
∑m
k
⎡A⎤
⎢⎣ m ⎥⎦
k =1
∆v
µ0 M × ar
4π R 2
dv'
⎞
⎛B
∇ × ⎜⎜ − M ⎟⎟ = J
⎠
⎝ µo
Ingegneria dei Sistemi Elettrici_5b
⎡A⎤
⎣⎢ m ⎥⎦
⎡A⎤
⎢⎣ m 2 ⎥⎦
33
Esaminando le relazioni precedenti si vede che
quando il campo si sviluppa nella materia,
↓
le cariche elettrostatiche e magnetiche, presenti
nella materia, interagiscono con i rispettivi campi
elettrostatici e magnetici alterandone la
distribuzione rispetto a quella che si avrebbe nel
vuoto.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
34
Per tenere conto di questo fenomeno fisico nelle
espressioni di: D e J si introducono
rispettivamente
• il vettore di polarizzazione o momento elettrico P
e
• il momento magnetico M .
Inoltre si noti come nelle relazioni dei modelli al
prodotto scalare corrisponde il prodotto
vettoriale.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
35
Si definisce una nuova grandezza fondamentale, l’intensità del
campo magnetico H :
B
H=
−M
µ0
⎡ A⎤
⎢⎣ m ⎥⎦
L’uso del vettore H consente di scrivere una equazione rotorica che
mette in relazione il campo magnetico e la distribuzione delle
correnti di circolazione in ciascun mezzo, senza dover specificare il
vettore di magnetizzazione M o la densità di corrente volumica J m .
Combinando questa equazione con ∇ × B / µo − M = J si ottiene:
(
)
⎡ A⎤
∇× H = J ⎢ 2 ⎥
⎣m ⎦
con J é la densità volumica nel vuoto delle correnti di circolazione.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
36
Le equazioni:
∇⋅ B = 0
e ∇× H = J
esprimono le due equazioni differenziali fondamentali della
magnetostatica.
La permeabilità del mezzo non compare esplicitamente in queste
due equazioni.
Calcolando l’integrale superficiale scalare di entrambi i membri
della seconda equazione si ha:
∫ (∇ × H )⋅ d s = ∫ J ⋅ d s
S
M. Usai
S
Ingegneria dei Sistemi Elettrici_5b
37
e applicando il teorema di Stokes si ottiene:
∫ H ⋅ d l = I [ A]
C
dove:
• C é il contorno che delimita la superficie S e
• I é la corrente totale di circolazione che attraversa la superficie S.
Le direzioni di C e del flusso della corrente seguono la regola
della mano destra.
Questa relazione é un’altra espressione della legge della
circuitazione di Ampere per la quale: la circuitazione della
intensità del campo magnetico lungo un percorso chiuso, é
uguale al flusso delle correnti di circolazione attraverso la
superficie delimitata dal percorso.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
38
La legge della circuitazione é molto utile per la determinazione di
campi magnetici dovuti alla corrente, quando esistono simmetrie
cilindriche, cioè quando esiste un percorso chiuso intorno alla
corrente nel quale il campo magnetico é costante.
Quando le proprietà magnetiche del mezzo sono lineari e isotrope
la magnetizzazione é direttamente proporzionale alla intensità del
campo magnetico attraverso la relazione costitutiva:
M = χm H
dove χ m é un quantità adimensionale chiamata suscettibilità
magnetica.
M. Usai
Ingegneria dei Sistemi Elettrici_5b
39
M = χm H
e sostituendo nella relazione:
H=
B
−M
µ0
⎡ A⎤
⎢⎣ m ⎥⎦
⎡Wb ⎤
B = µ0 (1 + χ m )H = µ0 µr H = µH ⎢ 2 ⎥
⎣m ⎦
µ
dove: µr = 1 + χ m =
µ0
o
1
⎡ A⎤
H= B ⎢ ⎥
µ
⎣m⎦
µr = permeabilità relativa del mezzo
µ0 = permeabilità del vuoto
µ = permeabilità assoluta del mezzo
M. Usai
Ingegneria dei Sistemi Elettrici_5b
40
Si sono così trovate delle relazioni analoghe tra le grandezze
elettrostatiche e quelle magnetostatiche, in base alle quali la
maggior parte delle equazioni che legano le grandezze fondamentali
in elettrostatica possono essere convertite nelle corrispondenti
relazioni analoghe nella magnetostatica.
M. Usai
• Elettrostatiche
• Magnetostatiche
E
B
D
ε
H
1/ µ
P
−M
ρ
V
⋅
×
J
A
×
⋅
Ingegneria dei Sistemi Elettrici_5b
41











