I Triangoli e i criteri di congruenza
1 Le caratteristiche di un triangolo
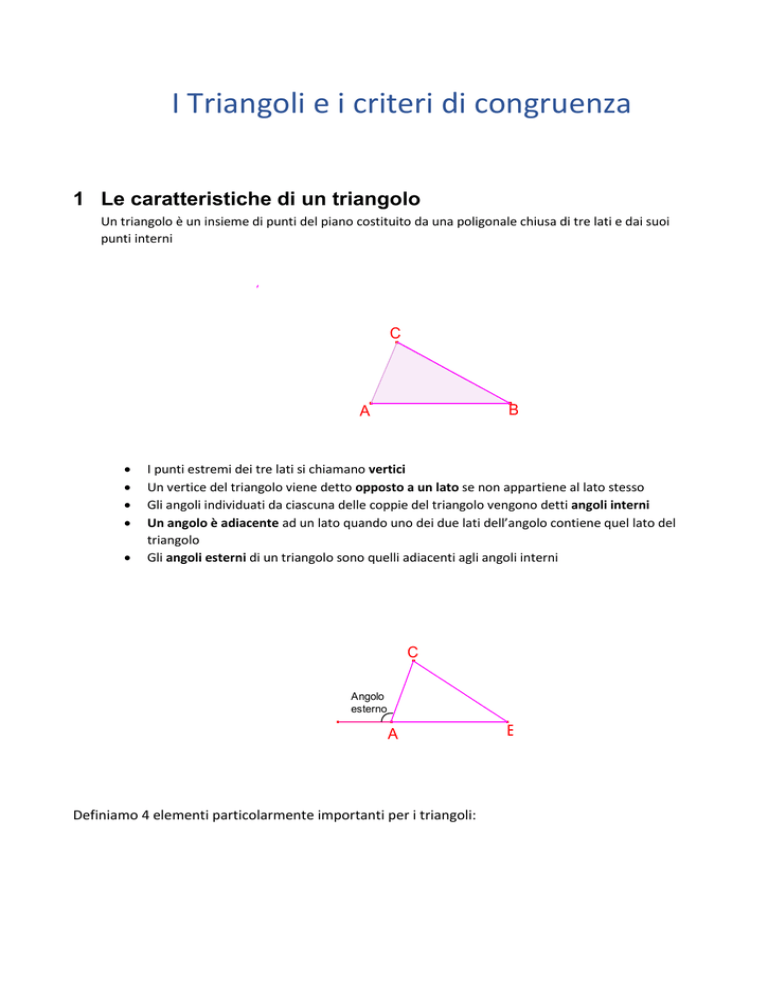
Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi
punti interni
C
B
A
I punti estremi dei tre lati si chiamano vertici
Un vertice del triangolo viene detto opposto a un lato se non appartiene al lato stesso
Gli angoli individuati da ciascuna delle coppie del triangolo vengono detti angoli interni
Un angolo è adiacente ad un lato quando uno dei due lati dell’angolo contiene quel lato del
triangolo
Gli angoli esterni di un triangolo sono quelli adiacenti agli angoli interni
C
Angolo
esterno
A
Definiamo 4 elementi particolarmente importanti per i triangoli:
B
1. In un triangolo ABC, la bisettrice relativa al vertice A è il segmento costituito dai punti della
bisettrice dell’angolo in A che sono anche punti del triangolo
C
A
B
Si dimostra che le bisettrici di un triangolo relative ai tre vertici si incontrano in unico punto
detto incentro.
C
Incentro
A
B
2. In un triangolo ABC, la mediana relativa a un lato è il segmento che ha per estremi il punto
medio del lato e il vertice opposto a quel lato
C
M
A
B
Si dimostra che le mediane di un triangolo, relative ai tre lati, si incontrano in un punto
detto baricentro
C
Baricentro
A
B
3. In un triangolo ABC, l’altezza relativa a un lato è il segmento che, partendo dal vertice
opposto al lato, incontra il lato stesso formando con esso due angoli retti
C
A
B
H
Si dimostra che le altezze relative ai tre lati del triangolo si incontrano in un punto detto
ortocentro.
C
Ortocentro
A
B
H
4. In un triangolo ABC, l’asse di un lato è quella retta che taglia il lato perpendicolarmente
(formando un angolo retto)
C
A
M
B
Si dimostra che gli assi di un triangolo si incontrano in un punto chiamato circocentro
C
Circocentro
A
M
B
Successivamente quando si studieranno le proprietà dei cerchi circoscritti ed inscritti ad un
triangolo vedremo le proprietà degli elementi appena introdotti.
Possiamo classificare i triangoli rispetto ai lati:
Triangolo
equilatero
Triangolo
isoscele
Triangolo
scaleno
o rispetto agli angoli:
Cateto
Ipotenusa
Cateto
Triangolo
rettangolo
Triangolo
ottusangolo
Triangolo
acutangolo
2 I Criteri di congruenza dei triangoli
Due triangoli sono congruenti se essi sono sovrapponibili.
Esistono dei criteri che permettono di stabilire quando due triangoli sono congruenti.
Primo Criterio di congruenza dei triangoli
Se due triangoli hanno ordinatamente congruenti due lati e l’angolo fra essi adiacenti,
allora sono congruenti
Secondo Criterio di congruenza dei triangoli
Se due triangoli hanno ordinatamente congruenti un lato e i due angoli a esso
adiacenti, allora sono congruenti
Terzo Criterio di congruenza dei triangoli
Se due triangoli hanno ordinatamente congruenti i tre lati allora sono congruenti.
I tre criteri di congruenza permettono di dimostrare una serie di proprietà sul triangolo
isoscele:
C
A
M
B
Se un triangolo è isoscele, allora ha due angoli congruenti
Se un triangolo ha due angoli congruenti, allora è isoscele
Se un triangolo è isoscele, allora la bisettrice dell’angolo è anche altezza mediana
rispetto alla base
Sempre attraverso i criteri di congruenza si riescono a dimostrare altre proprietà sui
triangoli:
In ogni triangolo non equilatero, a lato maggiore si oppone angolo maggiore
In un triangolo ogni angolo esterno è maggiore di ciascuno dei due angoli interni
non adiacenti ad esso.
In ogni triangolo un lato è minore della somma degli altri due. (questa è la così detta
disuguaglianza triangolare e permette, date tre segmenti, di stabilire se essi
possono essere i lati di un triangolo
3 Rette parallele e perpendicolari
Il V° postulato di Euclide permette di dimostrare tutta una serie di proprietà sui triangoli. Prima di
illustrarle occorre dare una serie di definizioni e proprietà sulle rette.
Rette perpendicolari
Due rette incidenti sono perpendicolari quando dividono il piano in due angoli retti
Si dimostra che per un punto del piano passa una e una sola retta perpendicolare a una retta data
Rette parallele
Due rette sono parallele quando non hanno alcun punto in comune
Per studiare la proprietà delle rette perpendicolari occorre definire gli angoli che due rette
formano con una trasversale che le taglia
2 1
3 4
6 5
7 8
Si danno le seguenti definizioni per gli angoli:
(4;6), (3;5) alterni interni
(1;7), (2;8) alterni esterni
(1;5), (2;6), (4;8), (2;6), (3;7) corrispondenti
(4;5), (3;6) coniugati interni
(1;8), (2;7) coniugati esterni
Usando queste definizioni e possiamo provare il seguente teorema:
Criterio di parallelismo tra due rette
Se due rette, incontrandone una terza, formano:
Angoli alterni congruenti oppure
Angoli corrispondenti congruenti oppure
Angoli coniugati supplementari (la somma è un angolo piatto)
Allora le due rette sono parallele
A partire dal V° postulato di Euclide si può dimostrare l’esistenza di un’unica retta parallela ad una
retta data e tutta un’altra serie di proprietà relative alle rette e ai triangoli:
Data una retta e un punto fuori di essa, è unica la retta passante per quel punto e parallela
alla retta data.
Se due rette sono parallele, formano con una qualunque trasversale angoli alterni
congruenti, angoli corrispondenti congruenti e angoli coniugati supplementari
In ogni triangolo ogni angolo esterno è congruente alla somma dei due angoli interni non
adiacenti ad esso
La somma degli angoli interni di un triangolo qualunque è congruente a un angolo piatto
La somma degli angoli interni in un poligono convesso di n lati è congruente a (n-2) angoli
piatti.
La somma degli angoli esterni di un poligono convesso è congruente a un angolo giro
Le ultime proprietà dimostrate permettono di aggiungere un criterio di congruenza per i triangoli
rettangoli.
4 I criteri di congruenza dei triangoli rettangoli
I tre criteri di congruenza si possono ridefinire per i triangoli rettangoli
Primo criterio triangoli rettangoli
Due triangoli rettangoli sono congruenti se hanno rispettivamente congruenti i due cateti
(conseguenza I° criterio generale di congruenza)
Primo criterio triangoli rettangoli
Due triangoli rettangoli sono congruenti se hanno congruenti rispettivamente un cateto e un
angolo acuto corrispondenti (conseguenza II° criterio generale di congruenza)
Terzo criterio triangoli rettangoli
Due triangoli rettangoli sono congruenti se hanno congruenti rispettivamente l’ipotenusa e un
angolo acuto (conseguenza II° criterio generale di congruenza)
Quarto criterio triangoli rettangoli
Due triangoli rettangoli sono congruenti se hanno congruenti rispettivamente l’ipotenusa e un
cateto











