Lezione n. 3
• Circuiti con sorgenti sinusoidali.
• Potenza elettrica in regime sinusoidale
• Condensatori e reattanza dei condensatori
• Induttori e reattanza degli induttori
• Trasformatori
• Soluzione di circuiti con sorgenti sinusoidali
• Segnali continui e discreti
• Segnali digitali
Why ac?
You might wonder why ac is even used. Isn’t it a lot more complicated than dc? Well, ac is easy to generate from turbines, as you’ve just seen. Rotating coil‐and magnet devices always produce ac, and in order to get dc from this, rectification and filtering are necessary. These processes can be difficult to achieve with high voltages. Alternating current lends itself well to being transformed to lower or higher voltages, according to the needs of electrical apparatus. It is not so easy to change dc voltages. Electrochemical cells produce dc directly, but they are impractical for the needs of large populations. To serve millions of consumers, the immense power of falling or flowing water, the ocean tides, wind, burning fossil fuels, safe nuclear fusion, or of geothermal heat are needed. (Nuclear fission will work, but it is under scrutiny nowadays because it produces dangerous radioactive by‐products.) All of these energy sources can be used to drive turbines that turn ac generators.
Technology is advancing in the realm of solar‐electric energy; someday a significant part of our electricity might come from photovoltaic power plants. These would generate dc.
Thomas Edison is said to have favored dc over ac for electrical power transmission in the early days, as utilities were first being planned. His colleagues argued that ac would work better. It took awhile to convince Mr. Edison to change his mind. He eventually did. But perhaps he knew something that his contemporaries did not foresee.
There is one advantage to direct current in utility applications. This is for the transmission of energy over great distances using wires. Direct currents, at extremely high voltages, are transported more efficiently than alternating currents. The wire has less effective resistance with dc than with ac, and there is less energy lost in the magnetic
fields around the wires. Direct‐current high‐tension transmission lines are being considered for future use. Right now, the main problem is expense. Sophisticated power‐conversion equipment is needed. If the cost can be brought within reason, Edison’s original sentiments will be at least partly vindicated. His was a long view. Circuiti con sorgenti sinusoidali .
Una sorgente sinusoidale è un dispositivo che fornisce ai suoi terminali una tensione o una
corrente che varia sinusoidalmente nel tempo.
20 V
L'ampiezza di un'onda sinusoidale viene chiamata
anche valore di picco (VP)
15 V
10 V
0V
A
25
0
37.5
50.0
t (μs)
-10 V
-15 V
20 V
-20 V
15 V
T
10 V
Vrm
0V
-10 V
-15 V
-20 V
0
VPP
25
s 37.5
50.0
t (μs)
La tensione di un'onda sinusoidale può
essere specificata anche con la tensione
picco picco o con il valore efficace (rms) .
Il picco picco è due volte il valore di picco.
Il valore rms è 0,707 volte il valore di
picco
Il valore efficace di una tensione (corrente) alternata è il valore di tensione
(corrente continua ) che dissiperebbe la stessa potenza su una resistenza.
*
Circuiti con sorgenti sinusoidali .
Frequenza (f) è il numero di cicli che un'onda sinusoidale completa in un secondo. La frequenza è misurata in Hz
Se 3 cicli di un'onda si verificano in un secondo, la frequenza è 3Hz
1.0 s
Il periodo e la frequenza sono reciproci uno dell’altro.
1
f =
T
1
T=
f
Circuiti con sorgenti sinusoidali .
Misure angolari
Le misure angolari possono essere effettuate in gradi (o) o radianti. Il radiante
(rad) è l'angolo che si forma quando l'arco è uguale al raggio di un cerchio. Ci
sono 360o o 2p radianti in un giro completo.
1.0
0.8
R
0.6
0.4
0.2
R
0
-0.2
0
π
π
4
2
3π
4
π
5π
4
3π
2
7π
4
2π
-0.4
-0.6
-0.8
-1.0
Poiché ci sono 2π radianti e 360o in un giro completo si possono dedurre le
seguenti relazioni:
rad =
2π rad
× degrees
360°
deg =
360°
× rad
2π rad
Circuiti con sorgenti sinusoidali .
Equazione onda sinusoidale
I valori istantanei di un'onda sono indicati con v o i. L'equazione per la tensione
istantanea (v) di un'onda sinusoidale è:
t
⎛
v = Vp sin (θ ) = Vp sin ⎜ 2π
⎝ T
⎞
⎟ = Vp sin ( 2π ft )
⎠
Dove:
Vp =
Tensione di picco
θ =
Angolo in radianti o gradi
Se la tensione di picco è 25 V, la tensione istantanea a 50 gradi è 19.2 V
90°
Vp
Vp = 25 V
v = Vp sin = 19.2 V
= 50°
0°
50°
Vp
Circuiti con sorgenti sinusoidali .
Variazione di fase
Angolo che specifica la posizione di un'onda sinusoidale rispetto ad un riferimento. Per
mostrare che un'onda sinusoidale viene spostato a sinistra o a destra di questo riferimento,
viene aggiunto un termine all'equazione vista in precedenza.
v = VP sin (θ ± φ )
Dove:
φ=
Variazione di fase
Esempio 1: ritardo di fase
Reference
40
Peak voltage
Voltage (V)
30
v = 30 VP sin (θ − 45o)
20
10
0
0°
45°
90°
135° 180°
225°
-20
-30
- 40
Angle (°)
270°
315°
360°
405°
Circuiti con sorgenti sinusoidali
Esempio 2: Anticipo di fase
Reference
40
Peak voltage
30
v = 30 VP sin (θ + 45o)
Voltage (V)
20
10
-45°
0 0°
-10
-20
45°
90° 135°
180°
225°
-30
-40
Angle (°)
270°
315°
360°
Potenza elettrica in regime sinusoidale
Se a una sorgente sinusoidale è collegato un resistore su di esso scorrerà una corrente
sinusoidale con frequenza e fase identica a quella della sorgente di tensione. Correnti che
variano sinusoidalmente con il tempo sono chiamate correnti alternate o ac (alternating
currents).
( v (t ) )
p(t ) = v (t )i (t ) =
La potenza ceduta al resistore istante per istante è:
v (t ) = VP ⋅ Sin[ω ⋅ t ]
1
0.5
0.8
0
−0.5
−1
0
0.2
0.4 0.6
t @sD
0.8
La potenza media ceduta al resistore è: P =
Valore efficace V =
rms
VP
2
1
2
Valore medio
T = 0.5 s
1
Sin HωtL2
Sin HωtL
T = 1s
R
VP2 ⋅ Sin[ω ⋅ t ]2
=
R
2
1
2
0.6
0.4
0.2
0
1
0
0.2
0.4
0.6
t
2
2
1 VP Vrms
⋅
=
2
R
R
0.8
1
Circuiti con sorgenti sinusoidali .
Modello idraulico per le correnti alternate
CONDENSATORI
Nei circuiti elettronici, il condensatore svolge un ruolo fondamentale, esso si oppone alle
variazioni in tensione e costituisce un circuito aperto in continua.
DIELETTRICO
La proprietà fondamentale del condensatore è di accogliere e di
conservare cariche elettriche, che prende il nome di capacità.
d
S
ΔQ
C=
ΔV
ΔQ carica elettrica espressa in Coulomb (C)
ΔV variazione di tensione espressa in Volt (V)
Unità di misura: Farad (F) o sottomultipli
ARMATURE
S
C = ε0 ⋅εr ⋅
d
ΔQ = C ⋅ Δ V
I=
1F =
1C
1V
Il valore capacitivo è determinato dalla superficie delle armature (S),
la loro distanza (d) e dalla natura del dielettrico interposto (ε0εr).
Si ottiene che la variazione di carica in un condensatore è determinata
da C e dalla variazione di tensione .
ΔQ
ΔV
=C⋅
Δt
Δt
dQ
dV
I (t ) =
=C⋅
dt
dt
La variazione di carica nell’intervallo di tempo Δt è pari alla corrente
Per ΔtÆ0 la corrente è proporzionale alla derivata della tensione CONDENSATORE
VVSS
Processo di carica…
Leads
−
Carica
Inizialmente
completa
scarico
Sorgente
rimossa
−
−
−
++
−++
+
+++−
−++
+++
+++
−
− −++
+
++
+
−++−
+
+
+
AA +
A
−
− +
Dielectric
−
−−
+−+
Plates
−−−
−
+−
+
−
− −
−
+−
−
−+ − Electrons
−
−−
−
−− B
+−
−
BB
−
−
−
−
Un condensatore con carica immagazzinata può lavorare come una batteria
temporanea.
CONDENSATORI
Condensatori in circuiti dc
Quando un condensatore è caricato
attraverso un resistore serie e una
sorgente dc la curva di carico è
esponenziale.
R
I
Vfinal
0
t
(a) Capacitor c harging voltage
Iinitial
C
0
(b) Charging current
t
CONDENSATORI
Condensatori in circuiti dc
Quando un condensatore è scaricato
attraverso un resistore la curva di
scarica è un esponenziale (corrente
negativa)
t
0
(a) Capacitor disc harging voltage
−Iinitial
R
I
Vinitial
C
0
t
(b) Disc harging current
CONDENSATORI
Curva esponenziale universale
τ = RC
100%
95%
98%
99%
86%
80%
Percent of final value
I valori specifici di
corrente e di tensione
possono essere letti da
una curva universale.
Per un circuito RC, la
costante di tempo è
Rising exponential
63%
60%
40%
37%
Falling exponential
20%
14%
5%
0
0
1τ
2%
2τ
3τ
4τ
Number of time constants
1%
5τ
CONDENSATORI
Condensatori a pellicola: Realizzati mediante un sandwich di strati
conduttivi e di dielettrico arrotolati, connessi opportunamente ed
incapsulati.
Condensatori Ceramici: Utilizzati in generale per alte frequenze, con
dielettrico costituito generalmente da una massa ceramica, la cui
costante dielettrica può essere variata tra 10 e 50.000.
Condensatori Elettrolitici: Il dielettrico è costituito
da un sottilissimo strato di ossido, realizzato
direttamente sul metallo (l'alluminio) che fa da
armatura e costituisce il terminale positivo. Il
terminale negativo è costituito da un elettrolita
(soluzione salina od acida), e da un secondo
elettrodo metallico .
CONDENSATORE
Modello idraulico di un condensatore
Capacitance
A capacitor stores energy in the form of an electric field that is established by the opposite charges on the two plates. The energy of a charged capacitor is given by the equation
W=
1
CV 2
2
where
W = the energy in joules
C = the capacitance in farads
V = the voltage in volts
CONDENSATORI
Condensatori in circuiti dc
Se una forma d’onda quadrata è
applicata, per le tensioni si
ottengono andamenti esponenziali.
VS
Qual’è la forma d’onda della corrente?
VC
R
VS
C
La corrente ha la medesima forma di VR.
VR
CONDENSATORI
Universal exponential curves
The universal curves can be applied to general formulas for
the voltage (or current) curves for RC circuits. The general
voltage formula is
v =VF + (Vi − VF)e−t/RC
VF = final value of voltage
Vi = initial value of voltage
v = instantaneous value of voltage
The final capacitor voltage is greater than the initial
voltage when the capacitor is charging, or less that the
initial voltage when it is discharging.
Chapter 2
Summary
Capacitive reactance
Capacitive reactance is the opposition to ac
by a capacitor. The equation for capacitive
reactance is
XC =
1
2πfC
The reactance of a 0.047 μF capacitor when a
frequency of 15 kHz is applied is 226 Ω
Principles of Electric Circuits, Conventional Flow, 9th ed.
Floyd
© 2010 Pearson Higher Education,
Upper Saddle River, NJ 07458. • All Rights Reserved
INDUTTORI
Presenta un comportamento opposto a quello del
condensatore. Si oppone alle variazioni in corrente
e costituisce un cortocircuito in continua.
l
A
N
I
In un induttore su cui scorre una corrente variabile,
+
V I(t) , è generato un campo magnetico variabile che
si oppone alle variazioni della corrente che lo attraversa. Maggiore è la frequenza
maggiore è l’effetto di opposizione.
V (t ) = L ⋅ dI
dt
La tensione è proporzionale alla derivata della corrente L è denominata coefficiente di auto‐induzione o induttanza
L [H= Vs/A] dipende da 3 fattori :
•
Il quadrato del numero di spire.
•
La configurazione geometrica del flusso magnetico (A/l).
•
Proprietà magnetiche del materiale intorno a cui sono avvolte le spire.
INDUTTORI
Simboli comuni per l’induttore sono
Air core
Iron core
Componenti in tecnologia TH
Ferrite core
Variable
Componenti in tecnologia SM
Summary
Self Inductance
The induced voltage is given by the formula vind = L
di
dt
What is the inductance if 37 mV is induced
across a coil if the current is changing at a rate of
680 mA/s?
di
vind = L
dt
Rearranging,
vind
0.037 V
L=
=
= 54 mH
di
0.68 A/s
dt
INDUTTORI
Alle alte frequenze i componenti reali hanno un
comportamento diverso da quello ideale.
|Z| di un generico induttore in funzione della
frequenza.
Gli effetti parassiti a frequenze elevate modificano
il comportamento dell’elemento:
C
• Capacità parassite legate alla struttura.
• Resistenze legate alla struttura e ai reofori .
• Resistenze legate alle perdite del core.
C
C
L
Rp
Q≅
ω LS
Rs
INDUTTORI
Viniziale
Induttori in circuiti dc
Quando un induttore è collegato in
serie con un resistore e una sorgente
dc, il cambiamento di corrente è
esponenziale.
t
Tensione dell’induttore dopo chiusura interruttore
IFinale
R
L
t
Corrente dell’induttore dopo chiusura interruttore
INDUTTORI
Induttori in circuiti dc
Le stesse forma sono ottenute se
viene utilizzato un onda quadra
per l'origine.
VS
VL
R
VS
L
VR
Summary
Universal exponential curves
L
τ=
R
100%
95%
98%
99%
86%
80%
Percent of final value
Specific values for
current and voltage
can be read from a
universal curve. For
an RL circuit, the
time constant is
Rising exponential
63%
60%
40%
37%
Falling exponential
20%
14%
5%
0
0
1τ
2%
2τ
3τ
4τ
Number of time constants
1%
5τ
Summary
Universal exponential curves
The curves can give
specific information
about an RL circuit.
Read the rising
exponential at the
67% level. After 1.1 τ
95%
99%
63%
60%
40%
37%
20%
14%
5%
0
0
98%
86%
80%
Percent of final value
In a series RL circuit,
when is VR > 2VL?
100%
1τ
2%
2τ
3τ
4τ
Number of time constants
1%
5τ
Summary
Universal exponential curves
The universal curves can be applied to general formulas for
the current (or voltage) curves for RL circuits. The general
current formula is
i =IF + (Ii − IF)e−Rt/L
IF = final value of current
Ii = initial value of current
i = instantaneous value of current
The final current is greater than the initial current
when the inductive field is building, or less than the initial
current when the field is collapsing.
Summary
Inductive reactance
Inductive reactance is the opposition to
ac by an inductor. The equation for
inductive reactance is
X L = 2πfL
The reactance of a 33 μH inductor when a
frequency of 550 kHz is applied is 114 Ω
INDUTTORI
Modello idraulico di un induttore
Si consideri un volano applicato ad una turbina
in linea con un flusso d'acqua.
Se l'acqua scorre costantemente in una
direzione, dopo un intervallo
di tempo
(transitorio), turbina e volano vanno a regime
e non presentano più resistenza al flusso
dell’acqua .
Nel caso di regime alternato l’acqua scorre
avanti e indietro e il sistema turbina/volano,
nell’invertire alternativamente il verso di
rotazione, presenta una resistenza che
aumenta all’aumentare della frequenza del
regime alernato .
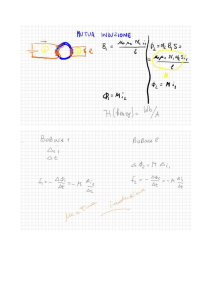
TRASFORMATORI
Quando una corrente AC scorre attraverso un induttore e un secondo induttore, chiuso
su un resistore, è posto così che il campo magnetico generato dal primo induttore
attraversi le sue spire, su di esse sarà indotta una tensione.
Tale fenomeno è descritto dal
parametro di mutua induttanza M
[Henry].
M dipende da molti fattori:
•
•
•
•
posizioni relative ,
distanza l'uno dall'altro,
dimensione e forma dei due induttori,
permeabilità del nucleo dei due induttore e dello spazio tra di loro.
Risulta: M = k L1L2
L1 e L2 sono le induttanze dei due induttori accoppiati (in henry),
k è il coefficiente di accoppiamento al massimo pari ad uno.
Nelle bobine su nucleo di ferro quasi tutte le linee di forza, del campo magnetico
dell’induttore primario, attraversano l’induttore secondario garantendo un k ≈1.
La condizione k ≈1 rende la tensione indotta indipendente dall’induttanza dei due
induttori.
TRASFORMATORI
La tensione indotta sul secondario dipende dal
numero di spire che costituiscono i due induttori.
V2 = V1
N2
N1
+
V1
‐
RL +
V2
‐
Considerando nulle le perdite di potenza sul trasformatore esso trasferisce solo potenza, per
cui se il livello di tensione sul secondario cresce di N2/N1, il livello di corrente sul secondario
deve diminuire di N1/N2 , pertanto:
N
I2 = I1 1
N2
Sorgenti di segnale per l’induttore primario possono essere le linee elettriche
domestiche a 220 V, forme d’onda a frequenze audio o correnti RF.
Soluzione di circuiti con sorgenti sinusoidali
Per risolvere circuiti con sorgenti sinusoidali si può utilizzare una tecnica che permette di
trattare condensatori ed induttori in modo analogo ai resistori. Tale tecnica permette di
semplificare il processo di analisi.
In presenza di più sorgenti si applica il principio della sovrapposizione degli effetti.
In un circuito lineare con sorgente sinusoidale, su ogni componente sono presenti
tensioni e correnti sinusoidali con la medesima frequenza della sorgente.
• Ampiezza delle tensioni e delle correnti incognita,
?
• Fase delle tensioni e delle correnti incognita.
?
T
VP
VP1=?
t
T Δt=?
VP ⋅ cos (ωt )
ωt = 2π ft =
VP1 ⋅ cos (ωt + ϕ1 )
2π
t = ang .
T
Soluzione di circuiti con sorgenti sinusoidali - Fasori.
V1 e ϕ1 ,grandezze reali, sono le incognite da trovare.
Per semplificare l’analisi si utilizzano numeri complessi.
Numeri reali
Numeri complessi
V (t ) = VP ⋅ cos(ωt + ϕ ) + jVP ⋅ sin (ωt + ϕ )
Derivata
Integrale
= VP ⋅ e
j (ωt +ϕ )
= VP ⋅ e jϕ e jωt
d
(VP ⋅ cos(ωt + ϕ ) )
dt
jω ⋅VP ⋅ e jϕ ⋅ e jωt
∫V
VP ⋅ e jϕ
⋅ e jωt
jω
P
⋅ cos(ωt + ϕ )dt
V1 (t ) = V1 ⋅ cos(ωt + ϕ1 )
Fasore
Re ⎡⎣V1 ⋅ e jϕ1 ⋅ e jωt ⎤⎦
asse immaginario
VP ⋅ cos(ωt + ϕ )
VP
ϕ
t
V ⋅ cos(ωt )
ϕ
b
a
asse reale
Fasore 1.url
Fasore 2.url
Soluzione di circuiti con sorgenti sinusoidali.
Applicando il segnale V a un resistore condensatore e induttore.
VP0 ⋅ e jωt
VP0 ⋅ e jωt
VP0 ⋅ e jωt
P
P
P
VR = VP ⋅ e jωt
VC = VP ⋅ e jωt
Phase relationship.url
VL = VP ⋅ e jωt
Soluzione di circuiti con sorgenti sinusoidali.
Dividendo la tensione su ogni componente per la corrente che lo attraversa il
termine ejwt sparisce e si ottengono espressioni indicate come impedenze
funzioni della frequenza ma non del tempo:
VP ⋅ e jωt
ZR =
=R
VP jωt
⋅e
R
VP ⋅ e jωt
V
1
ZC =
=
=
I C jωCVP ⋅ e jωt jωC
V VP ⋅ e jωt
ZL = =
= jω L
jωt
I L VP ⋅ e
jω L
I, V e Z sono termini complessi e rispondono alle leggi viste in precedenza:
Legge di Ohm
V=ZI
Leggi di Kirckhoff
V=V1+…+VN e
Iin=Iout
Soluzione di circuiti con sorgenti sinusoidali
L’analisi elettrica, conoscendo il valore dei componenti e le grandezze impresse dai
generatori, permette di calcolare i valori delle correnti e tensioni applicate a tutti i
componenti del circuito.
Analisi elettrica di un circuito con N Componenti Sostituire il circuito dato con un circuito fittizio ottenuto introducendo le impedenze
corrispondenti (R‐>ZR, L‐>ZL, C‐>ZC ) e esplicitando la sorgente sinusoidale mediante il
corrispondente fasore.
V
+ V1 ‐
+ V2 ‐
Z1
Z2
I1 + V3 ‐
Z3
I3 4*N Incognite (N Re[V] + N Im[V]+
N Re[I] + N Im[I])
+ V5 ‐
I2 Z5
+ V4 ‐
Z4
I4
I5
+ V6 ‐
Servono 4*N relazioni
Z6
I6
Legge di Ohm 2N
relazioni
Leggi di Kirckhoff
2N
relazioni
Soluzione di circuiti con sorgenti sinusoidali
ϕR
VPR ⋅ cos (ωt + ϕ R )
ϕC
+ ‐
+
VP
1
R +
VPC ⋅ cos (ωt + ϕC )
VP ⋅ cos ωt
0.5
0
I p ⋅ cos(ωt + ϕ )
‐
VPC VPR
− 0.5
‐
−1
0
VPR , ϕ R
‐
+
V
‐
ZR
I
ZC
Esempio:
ZC =
+
VC
‐
π
3 π
2
2π
5π
2
3π
7π
2
4π
Fase
VPC , ϕC
VR
+ π
2
1
1
= = −j
jωC j
VR = IZR =
VC = IZC =
R = 1 ohm
ωC = 1 ohm
ZR = R = 1
1
1+ j
=
= 0.5 + j 0.5
1− j
2
−j
1− j
=
= 0.5 − j 0.5
1− j
2
I=
V
1
=
ZR + ZC 1 − j
VR
VC
Im 0.5
V
0.5
0.5
Re