MAGNETOSTATICA
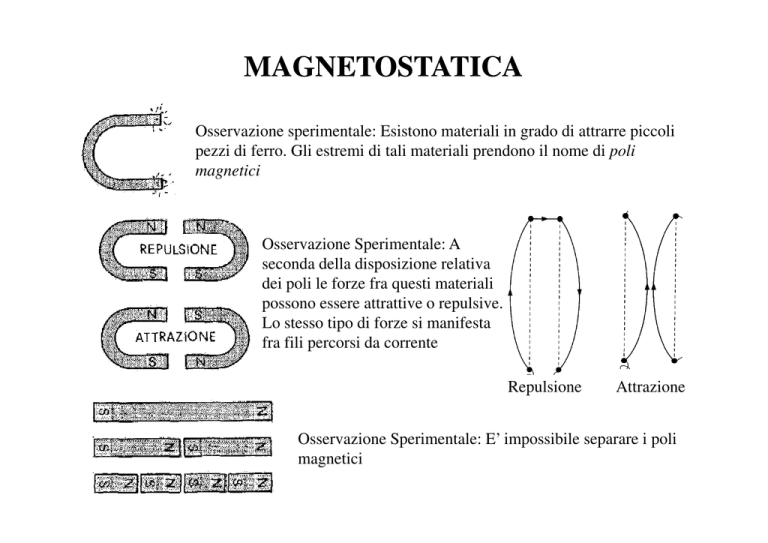
Osservazione sperimentale: Esistono materiali in grado di attrarre piccoli
pezzi di ferro. Gli estremi di tali materiali prendono il nome di poli
magnetici
Osservazione Sperimentale: A
seconda della disposizione relativa
dei poli le forze fra questi materiali
possono essere attrattive o repulsive.
Lo stesso tipo di forze si manifesta
fra fili percorsi da corrente
Repulsione
Attrazione
Osservazione Sperimentale: E’ impossibile separare i poli
magnetici
MAGNETOSTATICA
La forza per unità di lunghezza fra due fili percorsi da corrente risulta:
dF µ 0 I1 I 2
=
dl 2π d
µ0= 4π 10-7 N/A2
permeabilità magnetica del vuoto
In effetti l’Ampere è definito come la corrente che attraversa due fili conduttori lunghi 1 metro e
posti ad un metro di distanza fra di loro, che si attraggono con una forza di 1 Newton
MAGNETOSTATICA
Queste forze possono essere attribuite ad un campo di induzione magnetica B generato
da fili percorsi da corrente o da materiali magnetici. Utilizzando della limatura di ferro
è possibile ricostruire le linee del campo.
Le linee di campo sono linee chiuse
(campo solenoidale) e la forza
magnetica è perpendicolare al campo.
dF = Idl × B
II Legge di Laplace
MAGNETOSTATICA
Idl = (nqv ⋅ dS )dl = dNqv con dN = ndS ⋅ dl Numero di portatori di carica in dl
Posso quindi riscrivere la forza su di una carica in moto come:
F = qv × B
Quindi in generale in presenza di campi elettrici e magnetici una carica in
movimento subisce una forza pari a :
F = q(E + v × B )
Forza di Lorentz
Il vettore induzione magnetica quindi si misura nel Sistema Internazionale in:
Osservazione: il campo magnetico non compie lavoro sulle cariche
MAGNETOSTATICA
Spesso si utilizza però il Gauss
MAGNETOSTATICA
Il campo generato da un tratto dl di filo percorso da corrente è:
µ 0 dl × r
dB =
I 2
4π
r
I Legge di Laplace o Legge di Biot-Savart
La legge di Biot-Savart può essere riscritta in termini di densità di corrente come:
µ 0 J (r′)× (r − r′) 3
µ0
J (r′) 3
B=
d r=
∇× ∫
d r
3
∫
4π
4π
r − r′
r − r′
Da cui segue immediatamente:
∇⋅B = 0
E con un poco più di lavoro in condizioni stazionarie:
∇ × B = µ0 J
Quest’ultima può essere riscritta in forma integrale come:
∫ B ⋅ dl = µ ∫ J ⋅ dS
Γ
0
Σ
Legge di Ampere
MAGNETOSTATICA
Esempio: Spira percorsa da corrente
I diversi contributi danno un campo diretto lungo l’asse
Il campo ha la stessa forma di quello generato da un dipolo.
E’ identico al campo generato da un dipolo magnetico di
momento
m = πR 2 In












