magnetostatica - Simone Ercoli

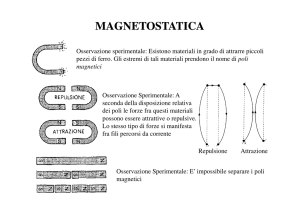
MAGNETOSTATICA
Potenziale vettore
Ricordiamo le seguenti identità
∇ × (∇f ) = 0
∇ ⋅ (∇ × v ) = 0
∇×E = 0
U : ∇U = − E
Poiché
⇒∃
∇⋅B = 0
A :∇× A = B
I potenziali U ed A non sono unici infatti U è definito a meno di una costante f0 mentre
A ′ = A + ∇f
soddisfa ancora l’equazione precedente. (Invarianza di gauge)
f0 viene utilizzata per annullare il potenziale all’infinito mentre f si può usare oltre che per
annullare A' all’infinito anche per annullare divA ' in tutto lo spazio. Per questo è
sufficiente risolvere:
∇ ⋅ A + ∇2 f = 0
Equazione che ammette una e una sola soluzione una volta fissate le condizioni al contorno
MAGNETOSTATICA
Potenziale vettore
Se ammettiamo
∇ ⋅ A = 0 allora diventa molto semplice scrivere:
µ 0 J = ∇ × B = ∇ × ∇ × A = ∇(∇ ⋅ A ) − ∇ 2 A = −∇ 2 A
O meglio:
∇ 2 A = − µ 0 J equazione generale del potenziale vettore
La cui soluzione formale è
Questa è analoga all’espressione
µ
A(r ) = 0
4π
V (r ) =
soluzione dell’equazione di Poisson
∫
1
4πε 0
∇ 2V = −
J (r′) 3
d r′
r − r′
ρ (r′)
∫ r − r′
ρ
ε0
d 3r ′
MAGNETOSTATICA
Esempio1: filo indefinito percorso da corrente
µI
B= 0
4π
∫
+∞
−∞
dl × ∆r
∆r
3
=
µ0 I
t
2π r
µ0 I  r 
A=−
ln k
2π  r0 
Esempio2:spira percorsa da corrente
µ 0 I dl × ∆r µ 0
πR 2 I
Bz =
=
k
3
3/ 2
∫
2
2
4π
2π (R + z )
∆r
µ 0 I dl µ 0 πR 2 In × r
A=
=
∫
4π r 4π
r2
MAGNETOSTATICA
Esempio3: Solenoide con n spire per unità di lunghezza
Sull’asse:
B = µ 0 nIi
MAGNETOSTATICA
In analogia con quanto avviene nei dielettrici, all’interno
dei materiali magnetici si trovano dei dipoli magnetici
elementari che si orientano seguendo il campo magnetico
esterno.
I mezzi nei quali i dipoli magnetici si orientano
parallelamente al campo esterno si dicono paramagnetici
I mezzi nei quali i dipoli magnetici si orientano
antiparalleli al campo esterno si dicono diamagnetici
In alcuni mezzi permane un orientamento anche dopo che
è stato rimosso il campo esterno, questi materiali si
chiamano ferromagneti ed in essi la magnetizzazione è
funzione non solo del campo presente ma anche della
storia passata del mezzo (memorie magnetiche).
MAGNETOSTATICA
In analogia con quanto già fatto per i mezzi dielettrici possiamo riscrivere le equazioni di
Maxwell per il campo magnetico nei mezzi introducendo una densità di corrente
microscopica del mezzo Jm:
∇⋅B = 0
∇ × B = µ0 (J + J m )
E , sempre in analogia con i dielettrici, introduciamo un vettore polarizzazione magnetica M
come prodotto della densità di dipoli microscopici n per il valor medi del dipolo m
M = nm
MAGNETOSTATICA
Se interpretiamo i singoli dipoli come dovuti a delle spire
elementari allora nel caso di magnetizzazione uniforme la
densità di corrente Jms è confinata alla superficie, infatti i
contributi interni al volume del materiale si cancellano.
In questo caso la relazione con il vettore polarizzazione
magnetica è:
J ms = M × n
Questo non avviene nel caso di magnetizzazione
inomogenea per la quale vi è una densità di corrente residua
internamente al materiale Jmv. In questo caso la relazione con
il vettore polarizzazione magnetica è:
J mv = ∇ × M
MAGNETOSTATICA
Poiché le equazioni di Maxwell non sono adatte a descrivere le discontinuità dovute alle
superfici utilizziamo le correnti di volume Jmv.
∇ × B = µ0 (J + J mv ) = µ0 (J + ∇ × M )
E definendo
H=
1
µ0
B − M otteniamo
∇⋅B = 0
∇×H = J
In analogia con le corrispondenti equazioni per il campo elettrico
∇⋅D = ρ
∇×E = 0
Notiamo che l’equazione per H si può riscrivere in forma integrale
∫λH ⋅ dl = ∫ J ⋅ dS = ∑
Σ
i
Ii
Dove le Ii sono le correnti concatenate alla linea chiusa λ. Teorema di circuitazione di Ampere
MAGNETOSTATICA
E’ possibile scrivere una relazione semplice fra B,H ed M solo nei mezzi magnetici
omogenei ed isotropi. Nel qual caso i due vettori sono paralleli e vale:
B = µ H = µ0 µ r H
M = χmH
Con µ permeabilità magnetica, e χ m = µ − 1 suscettività magnetica
MAGNETOSTATICA
In presenza di una superficie di separazione fra due materiali
magnetici possiamo ricavare delle relazioni analoghe a quelle per i
vettori campo elettrico e induzione dielettrica.
 H t1 = H t 2

µ1 H t1 = µ 2 H t 2
 Bt1 µ1 = Bt 2 µ 2

 Bn1 = Bn 2
tan θ1 µ1
=
tan θ 2 µ 2
Legge di rifrazione del campo
magnetico
MAGNETOSTATICA
Nelle sostanze diamagnetiche la suscettività magnetica è negativa ed indipendente dalla
temperatura.
Nelle sostanze paramagnetiche la suscettività magnetica è positiva e
dipende dalla temperatura T e dalla densità ρ secondo la legge di Curie,
dove C è una costante che dipende dalle proprietà atomiche.
Cρ
χm =
T
Nelle sostanze ferromagnetiche la suscettività magnetica dipende dalla
storia passata del materiale. Si può disegnare una curva di isteresi.
Le sostanze ferromagnetiche divengono paramagnetiche al di sopra di una
temperatura critica detta temperatura di Curie.
MAGNETOSTATICA
Valori tipici della
µdl permeabilità relativa iniziale
µdm permeabilità relativa massima
Hc campo di coercizione
µ0Ms magnetizzazione di saturazione
wk lavoroper un ciclo (area della curva)
Tc temperatura di Curie