Fisica Generale per Informatica — 25 gennaio 2011
Nota Bene: Si raccomanda una scrittura leggibile e ordinata, si dovrà brevemente indicare il
ragionamento che ha portato all’uso di una certa formula o equazione, ciò che non è
comprensibile non verrà valutato.
1.
Due blocchi A e B sono disposti nel modo indicato in figura. Il blocco A ha una massa di 4.00
kg; il blocco B ha una massa di 18.0 kg. Il coefficiente di attrito dinamico fra i due blocchi A e B
vale 0.30; quello tra il blocco B ed il piano orizzontale vale 0.10.
Una forza F = 55.0 N è applicata al blocco B in direzione parallela al piano di appoggio MN.
A. Determinare l’accelerazione del blocco A.
B. Determinare la tensione della corda.
C. Determinare le energie cinetiche del blocco A e del blocco B dopo 0.50 s dall’inizio del
moto (si supponga che all’istante t=0 la velocità dei due blocchi sia nulla e che il blocco
B sia così lungo che A non cada). Si trascurino il peso della corda, gli attriti ed il
momento d’inerzia della puleggia.
F
M
A
B
N
2.
Una batteria da Vb = 12.0 V viene utilizzata per accendere 3 lampadine: L1, L2, L3.
L1 è una lampadina da 12 V e 6 W di potenza (cioè quando viene accesa fornendole una tensione
di 12 V dissipa 6 W), L2 ed L3 sono 2 lampadine uguali da 6 V e 5 W. L2 ed L3 sono collegate
in serie fra di loro, L1 e’ collegata in parallelo al gruppo di L2-L3. L’insieme delle 3 lampadine è
collegato alla batteria attraverso un cavo di rame bifilare (cioè costituito da 2 conduttori) lungo
20 m. Il cavo ha una sezione S = 0.3 mm2 per ogni conduttore.
a. Calcolare la resistenza delle 3 lampadine quando sono accese alla loro tensione
nominale.
b. Disegnare lo schema elettrico del sistema.
c. Sapendo che la resistività del rame è ρ = 17.5 10-9 Ω m calcolare la tensione ai capi di
L1 e la corrente circolante in L1.
3.
Una sfera conduttrice di raggio a = 10 cm è posta all’interno di un guscio conduttore sferico di
spessore trascurabile e raggio b = 20 cm. Sfera e guscio sono concentrici. Sfera e guscio sono
entrambi carichi, e le loro cariche nette valgono rispettivamente
Qs = 2.0 10-7 C
e
Qg = 3.0 10-7 C.
Calcolare:
a) la densità di carica elettrica presente su ognuna delle 3 superfici (faccia esterna del guscio,
faccia interna, superficie della sfera);
b) il potenziale Vg sulla superficie esterna del guscio (si ponga uguale a zero il potenziale
all’infinito);
c) l’energia elettrostatica immagazzinata nello spazio compreso fra la sfera e la parete interna del
guscio.
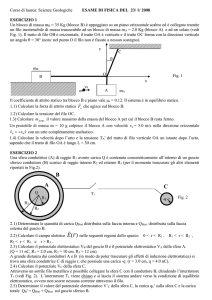
Soluzioni
1.
Possiamo utilizzare le leggi di Newton scrivendo le equazioni per i 2 blocchi. Poniamo un
sistema con l’asse X orizzontale che punta verso destra e l’asse Y verso l’alto.
Lungo l’asse Y la forza peso viene semplicemente bilanciata dalla reazione del vincolo che ci
permette solo di calcolare le forze di attrito.
Lungo l’asse X: su A agisce la tensione della fune che ne provoca il moto, inoltre i due blocchi si
scambiano una forza dovuta all’attrito: questa forza ha valore µAB mA g con µAB = 0.30. La forza si
oppone al movimento di A. Pero’ attenzione che questa forza agisce anche su B in senso opposto
(tende a trascinare B verso destra).
Su B agiscono inoltre la forza F che provoca il movimento, la forza di attrito tra B ed il piano che
vale µB (mA+mB) g ed è opposta al movimento, e la tensione della fune T. Quindi, possiamo
scrivere per la componente X delle forze:
per A:
T - mA µAB g
= m A aA
per B: -F + T + (mA + mB) g µB + mA µAB g = mB aB
poiché le 2 masse sono legate dalla fune, devono avere spostamenti uguali in modulo ma in
direzione opposta, per cui aA = - aB. Risolvendo le equazioni si ottiene facilmente:
aB = (-F + (mA + mB) g µB + 2 mA µAB g ) / (mA + mB)
aB = -0.45 m/s2
tensione della fune T = mA aA + mA µAB g = 13.6 N
Per calcolare le energie abbiamo bisogno delle velocità, poiché l’accelerazione è costante si tratta
di un moto uniformemente accelerato (V = v0 + a t) perciò:
V = 0.45 · 0.50 = 0.225 m/s, KA = ½ mA VA2 = 0.5 4.0 0.2252 = 0.10 J
e similmente KB = 0.46 J.
2.
Sapendo che V I = P (potenza) e V/ I = R si ottiene R = V2/ P, da cui
R(L1) = 122/ 6 = 24 Ω, analogamente R(L2) = 62 /5 = 7.2 Ω.
Lo schema e’ mostrato in figura, si noti che viene esplicitamente indicata la resistenza dei cavi.
+
R cavo
Vb
L2
L1
_
L3
R cavo
20 m
La resistenza del cavo e’ Rcavo = * lcavo / S = 17.5 10-9 * 20 / (0.3 10-6) = 1.17 Ω.
Per calcolare le correnti si possono scrivere le equazioni di Kirchhoff relative alle 2 maglie ma è
più semplice sfruttare le resistenze in serie parallelo: L2 ed L3 sono 2 resistenze in serie
R(L2-L3) = 7.2 + 7.2 = 14.4 Ω, in parallelo a L1:
1/(R(L1, L2, L3) = 1/R(L1) + 1/ R(L2-L3) = 1/24.0 + 1/14.4 da cui R(L1, L2, L3) = 9.0 Ω.
Questa resistenza è in serie alla resistenza del cavo (raddoppiata per tenere conto delle 2 Rcavo:
Rtotale = 1.17 + 9.0 + 1.17 = 11.34 Ω.
Per cui la corrente circolante nel cavo è I = 12.0 / 11.34 = 1.06 A.
Per trovare la tensione ai capi di L1 basterà togliere da Vb la caduta di tensione nelle 2 Rcavo:
V(L1) = Vb – 2 * I * Rcavo = 9.51 V.
La corrente circolante in L1 sarà V(L1) / R(L1) = 9.51 /24 = 0.40 A.
3.
a) Applichiamo il teorema di Gauss ad una superficie sferica interna al guscio. Poiche’ nel
conduttore del guscio non vi puo’ essere campo elettrico, applicando il teorema di Gauss si vede
immediatamente il flusso del campo elettrico e’ nullo e quindi la carica totale contenuta deve
essere zero, percio’ la carica presente sulla supeficie interna del guscio deve essere uguale ed
opposta a quella della sfera: chiamando σ la densita’ di carica superficiale si ottiene che:
σ(sfera) = Qs / (4a1.59 μC/m2, σ(interna guscio) = -Qs / (4b0.40 μC/m2,
σ(esterna guscio) =( Qs + Qg) / (4bμC/m2.
b) All’esterno del guscio (r > b):
E(r) = (1/40) (Qs+Qg)/r2
Vg = b E(r)dr = (1/40)(Qs+Qg)/b = 2.25 104 V
Questo poteva essere dedotto anche senza fare l’integrale perche’ abbiamo tre cariche sferiche
concentriche la cui somma e’: (Qs+Qg) ed a cui corrisponde quindi il potenziale di una carica
equivalente puntiforme, percio’, di nuovo e’: Vg = (1/40)(Qs+Qg)/b = 2.25 104 V
c) Fra la sfera e il guscio (a < r < b):
E(r) = (1/40) Qs/r2
uE(r) = ½ 0 E2(r) = (1/320) Qs2/r4 Integrando in coordinate sferiche si ottiene
U = ab uE(r) 4r2dr = (1/80) Qs2 ab 1/r2 dr = (1/80) Qs2 (1/a – 1/b) = 9.0 10-4 J
Questo risultato si poteva ottenere anche notando che le 2 sfere costituiscono un condensatore
sferico, per cui l’energia in esso contenuta e’ data U= Qs2 /2C dove C = 40 (a b) /(b-a) dove Qs e’
la sola carica contenuta sulle armature ( la carica sulla superficie esterna non contribuisce al
campo elettrico all’interno del guscio e quindi nemmeno all’energia elettrostatica.