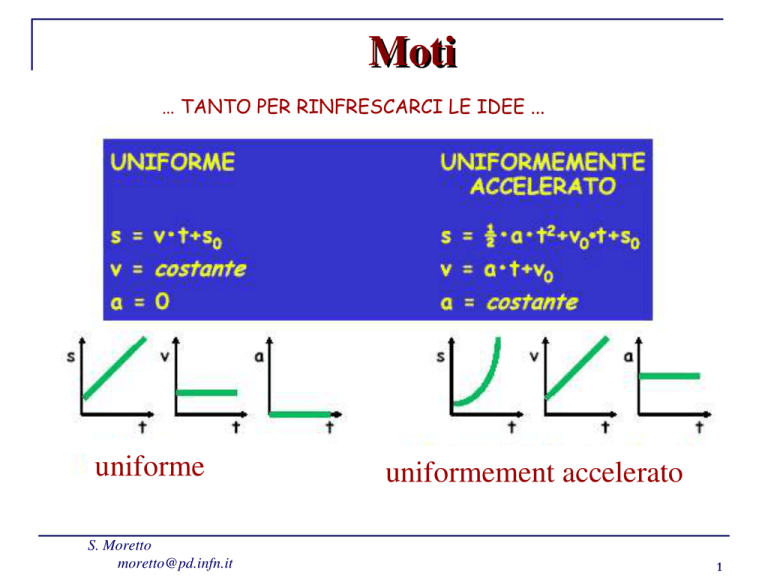
Moti
… TANTO PER RINFRESCARCI LE IDEE ...
uniforme
S. Moretto [email protected]
uniformement accelerato
1
Dinamica
Concetto di forza
I principi della dinamica
La forza peso
La gravitazione universale
Lavoro di una forza ed energia
Teorema delle forze vive
S. Moretto [email protected]
2
Il movimento: dal come al perche’
Per mettere in moto un corpo fermo
Per fermare un corpo in moto
Per variare un moto
bisogna intervenire dall’esterno
Variazione di moto
Causa esterna
Solo l’intervento di una causa esterna può
far iniziare un moto
far cessare un moto
far variare un moto (variando la velocità)
Una causa esterna non può essere altro che
una interazione con un “altro corpo”
es. interaz. a contatto sforzo muscolare, attrito, ecc.
interaz. a distanza gravità, attraz.magnetica, ecc.
S. Moretto [email protected]
3
Forza
Forza = qualunque causa esterna che produce una variazione dello stato di moto o di quiete di un corpo
Forza = vettore
La grandezza fisica “Forza”
Il dinamometro è uno strumento che sfruttando la
capacità di deformazione di una molla permette
eseguire una misura statica della forza.
S. Moretto [email protected]
Due pesi sono uguali se
producono lo stesso
allungamento della
molla, un peso doppio
triplo…infatti allunga la
molla del doppio,
triplo….Segnati questi
allungamenti si
costruisce una scala
graduata con cui misurare
una qualsiasi forza
incognita
4
Le leggi Newtoniane del moto
I0 Principio
(o legge d’inerzia):
un corpo non soggetto ad alcuna sollecitazione esterna mantiene il suo stato di quiete o di moto rettilineo uniforme
Esperienza: un corpo in moto dopo un po’ si ferma.
Ma sulla Terra nessun corpo è isolato: c’è sempre attrito.
Riducendo l’attrito si prolunga il moto.
Se non ci fosse attrito il moto continuerebbe all’infinito.
No forza No variazione stato di moto
No variazione di velocità No accelerazione
Quiete o moto rettilineo uniforme
S. Moretto [email protected]
5
Secondo Principio
II0 Principio
Un corpo soggetto a un sistema di forze la cui risultante sia diversa da zero è soggetto ad accelerazione
Esiste una proporzionalità
diretta tra forza risultante
applicata ed accelerazione
prodotta esprimibile
attraverso la relazione
S. Moretto [email protected]
F =m a
6
Secondo Principio: massa
La costante di proporzionalità m è una
grandezza riferita al corpo detta massa
inerziale
La massa è stata scelta come grandezza
fondamentale nel S.I
m si misura in kg (nel SI), g (10-3 kg) , ….
La forza è una grandezza derivata
F si misura in N (nel SI), 1N= 1kg m/s2 .
(Altre unità di misura per la forza: 1dyne=10-5N,
1kgp=9.8N)
S. Moretto [email protected]
7
Dal secondo principio:
•Quiete
Fris=0
•Moto rettilineo uniforme
•Moto rett. unif. Accelerato
S. Moretto [email protected]
Fris=0
Fris =costante
8
Terzo Principio
Se un corpo A esercita
una forza su un corpo B,
a sua volta B esercita su A
una forza uguale e contraria.
III0 Principio
Le forze non possono esistere isolate ; quando si manifesta una forza c’è
sempre il suo partner in qualche posto dell’universo
mA
FBA
A
FAB
mB
B
FAB
FAB= -FBA
S. Moretto [email protected]
9
Esempi per il terzo principio della dinamica
Le forze nascono sempre in coppia
Ciascuna forza della coppia è uguale ed opposta
all’altra forza ed ha la sua stessa linea d’azione
L’azione e la reazione sono tra loro interscambiabili
Es.
Esempi quotidiani:
- sostegno pavimento/sedia
- spinta “all’indietro”
- rinculo
- camminare, correre
- mezzi di trasporto
S. Moretto [email protected]
10
Forze di contatto e forze a distanza Un corpo fermo su un tavolo rimane fermo anche se sappiamo essere
sempre presente la forza peso
la risultante delle forze agenti è zero
N
p
E’ una forza di contatto quella che un muscolo che si contrae esercita
su un osso
+
Sono forze a distanza ad esempio la forza gravitazionale e la forza elettrica
S. Moretto [email protected]
11
Forze di contatto: la tensione e l’attrito
R
reazione: forza esercitata dal corpo sulla fune
fc forza esercitata dalla fune sulla massa m
mg
F1
Fa
F2
Corpo in tensione T=F1=F2
Fb
Corpo in compressione C=Fa=Fb
Una fune esercita sul corpo una forza di trazione T
T
T
T
T
T
S. Moretto [email protected]
T
12
Interazioni fondamentali
Tutte le forze sono riconducibili a 4 interazioni fondamentali
Gravitazionali
Interazione fra masse.
Attrattiva, raggio d’azione infinito
Domina la dinamica celeste.
forza peso ecc.
Interazioni fra cariche elettriche.
Attrattiva o repulsiva, raggio infinito.
Domina interazioni
atomiche/molecolari ecc.
Forti
Elettromagnetiche
Interazione fra quark. Molto complessa. Corto raggio
(<10-15 m) Domina struttura e interazioni nucleari,
dinamica stellare, primi istanti dell’universo
Interazione fra ‘cariche deboli’
Decadimento beta. Importante nella dinamica
stellare.
S. Moretto [email protected]
Deboli
13
Forza gravitazionale
Tra due corpi di massa m1 e m2, posti a distanza r, si esercita sempre non solo sulla Terra! una forza di attrazione
­diretta lungo la congiungente tra i due corpi
­proporzionale alle due masse
­inversamente proporzionale al quadrato della loro distanza
m1
r
m2
... troppo piccola per essere osservata tra corpi “normali” ...
S. Moretto [email protected]
14
Forza gravitazionale
LEGGE DI GRAVITAZIONE UNIVERSALE
F =
- G m1 m2 r
r2 r
attrazione
G = 6.67•10–11 N•m2/kg2
costante
di gravitazione universale
... troppo piccola per essere osservata tra corpi “normali” ...
S. Moretto [email protected]
15
Esempio forza gravitazionale
Quanto vale la forza gravitazionale tra due persone di massa m=
60 kg posti ad un metro?
F =G
¿
mM
r2
6 . 67⋅10 −1 1 Nm 2 / kg 2 ⋅ 60
kg ⋅ 60 kg
1 m 2
¿ 24⋅103⋅10−11 N =24⋅10−8 N
S. Moretto [email protected]
16
Esempio forza gravitazionale
Quanto vale la forza gravitazionale tra la Terra e un corpo
m
di massa m= 1 kg posto alla superficie della Terra?
F
Dati Terra: M = 5.98 •10 kg, R = 6.38 •10 m
24
F = G
6
R
M
mM
r2
6 . 67⋅10 −1 1 N m2 / kg 2 ⋅ 1
¿
2
6 . 3 8⋅10 6 m
kg ⋅ 5 . 98⋅10 24 kg
¿ 9 . 799 N
Risultato: 9.8 N
S. Moretto [email protected]
17
Accelerazione di gravita’
M m
F=G 2
r
F = mg
g = 9.8 m/s2
nelle vicinanze
della superficie della Terra
forza peso
g è un’accelerazione!
S. Moretto [email protected]
18
Forza peso
L’atmosfera terrestre regione di spazio vicina alla superficie della Terra
è sede di un campo di forza gravitazionale: ogni corpo di massa m che si trova in quella regione risente di una forza peso diretta verticalmente verso il basso.
forza peso
F = mg = p
S. Moretto [email protected]
modulo
direzione
verso
|p| = m g
verticale
basso
19
Accelerazione di gravità
E’ un dato sperimentale che gli oggetti, non sostenuti, cadono verso la terra. Si nota che spesso la velocità di impatto con il suolo cresce al crescere della altezza dalla quale tali oggetti cadono.
Aristotele (384­322 a.C.) sosteneva che i corpi pesanti
cadono più velocemente di quelli leggeri.
Galileo (1564­1642) per mezzo di osservazioni fatte a
Pisa fra il 1589 ed il 1592, trascurando l’effetto
dell’aria, affermò:
9. l’accelerazione di gravità è la stessa, per tutti gli oggetti che cadono, qualunque sia la loro grandezza o natura
10. l’accelerazione di gravità è costante
S. Moretto [email protected]
20
Accelerazione di gravità (II)
1. l’accelerazione di gravità è la stessa, per tutti gli oggetti che cadono, qualunque sia la loro grandezza o natura
2. l’accelerazione di gravità è costante
Queste due affermazioni non sono banali. Infatti l’esperienza di tutti i giorni dice che, ad esempio, le monete cadono più velocemente dei pezzi di carta
(disaccordo con 1) e che oggetti fatti cadere da grandi altezze S. Moretto raggiungono una velocità massima o velocità limite [email protected]
21
Accelerazione di gravità (III)
Tutto dipende dall’aria
Tutto dipende dall’aria. Utilizzando un cilindro nel quale sia possibile fare il vuoto (Tubo di Newton)
si possono dimostrare le due affermazioni:
4. l’accelerazione di gravità g è la stessa, per tutti gli oggetti che cadono, qualunque sia la loro grandezza o natura
5. l’accelerazione di gravità è costante
g = 9.8 m s-2
Al livello del mare
S. Moretto [email protected]
22
Accelerazione di gravità (IV)
Supponiamo di avere un corpo che venga fatto cadere, fermo, da un’altezza h=84 m. Calcolare il tempo di arrivo e la velocità di impatto.
Poiché agisce l’accelerazione di gravità g, il moto sarà
uniformemente accelerato. Possiamo quindi scrivere:
Indipendenti
dalla massa!!
S. Moretto [email protected]
23
Forza peso: Equazioni
MOTO DI CADUTA
sempre uniformemente accelerato
con accelerazione g = 9.8 m/s2
v = g t
h = ½ g t2
linee di forza
h
p
90°
suolo
Tempo di arrivo al suolo: t = 2h/g
Velocità di arrivo al suolo: v = 2gh
S. Moretto [email protected]
24
Massa, peso, densita’
m
MASSA
PESO
kg
p = mg
grandezza fondamentale
proprietà intrinseca dei corpi
N
forza con cui
ogni corpo dotato di massa
viene attirato dalla Terra
Unità di misura pratica: kgpeso = kgmassa•9.8 m/s2 = 9.8 N
DENSITA’
relazione tra massa e dimensioni dei corpi
utile soprattutto per liquidi e gas
massa
densità =
volume
S. Moretto [email protected]
d= m/V
kg/m3
Def. simile: concentrazione v. Chimica
25
Misure di densita’
d= m/V
kg/m3
g/cm3
kg/l
g/l
Es.
Densità dell’acqua:
1 g/cm3 = (10-3 kg)/(10-6 m3) = 103 kg/m3
= (10-3 kg)/(10-3 dm3) = (10-3 kg)/(10-3 l) = 1 kg/l
= (1 g)/(10-3 dm3) = (1 g)/(10-3 l) = 103 g/l
... e altri multipli e sottomultipli...
Equivalenze con densità (di uso comune in Medicina):
Es.
1 mg/dl = (10-3 g)/(10-1 dm3) = (10-3 g)/(102 cm3) = 10-5 g/cm3
1 g/mm3 = (10-6 g)/(10-3 cm3) = 10-3 g/cm3
S. Moretto [email protected]
ecc... (fantasia!)
26
Momento di una Forza
Momento di una forza
Il momento di una forza rispetto ad un centro O è un vettore
la cui direzione è perpendicolare al piano che contiene la forza ed il braccio b (direzione perpendicolare al foglio).
Il verso è dato dalla regola della mano destra.
Il suo modulo è M = bF dove b (detto braccio) indica la distanza tra il punto O e la retta che contiene la forza F. Il momento M rispetto al centro O è responsabile delle rotazioni intorno ad O. Se la retta passasse per O il momento M sarebbe nullo.
S. Moretto [email protected]
27
Equilibrio
Condizione di equilibrio:
Nel caso di un sistema rigido devono essere nulle:
la somma vettoriale di tutte le forze applicate
EQUILIBRIO TRASLAZIONALE
la somma vettoriale dei momenti di tali forze
EQUILIBRIO ROTAZIONALE
S. Moretto [email protected]
28
Lavoro
S. Moretto [email protected]
29
Lavoro
Il lavoro è una quantità scalare!
S. Moretto [email protected]
30
Lavoro
Riassumendo:
lavoro motore
lavoro resistente
S. Moretto [email protected]
31
Lavoro
S. Moretto [email protected]
32
Energia
L’energia si manifesta in forme diverse e si puo’ trasformare da una forma all’altra.
­ cinetica
­ potenziale gravità
­ potenziale elastica
­ potenziale elettrica
­ termica (calore)
Il lavoro compiuto su un corpo ­ chimica
diventa energia immagazzinata, ­ nucleare
cioe’ capacita’ di compiere ulteriore lavoro.
­ ...............
Energia = capacità potenziale di compiere
lavoro meccanico
stessa unità di misura del lavoro: joule
S. Moretto [email protected]
33
Principio di conservazione dell’Energia
PRINCIPIO DI CONSERVAZIONE DELL’ENERGIA
In un sistema isolato, l’energia totale rimane costante.
L’energia non si crea e non si distrugge: si trasforma!
S. Moretto [email protected]
34
Energia cinetica
Ogni corpo in movimento e’ dotato di energia
in base alla sua massa e alla sua velocita’
Energia cinetica: T = ½ mv2
Aumento di velocita’ = somministrazione di energia
S. Moretto [email protected]
35
Teorema delle forze vive
Il lavoro compiuto da una forza è pari alla variazione
dell’energia cinetica.
S. Moretto [email protected]
36
Problema
SI!
Solo se L è
diverso da zero!
S. Moretto [email protected]
37
Forze conservative e dissipative ­ 1
Una forza e’ conservativa se il lavoro
compiuto contro di essa per spostare un
corpo dal punto A al punto B non
dipende dal cammino seguito, ma solo
dalla posizione relativa dei punti A e B.
S. Moretto [email protected]
A
(1)
(3) (2)
B
38
Forze conservative e dissipative ­ 2
Definizione equivalente:
(1)
Una forza e’ conservativa se il lavoro
A
compiuto contro di essa per spostare
(3) (2)
un corpo dal punto A al punto B e’ uguale
e contrario al lavoro compiuto per farlo
B
ritornare da B a A, indipendentemente dal cammino
seguito. Quindi il lavoro di “andata e ritorno” lungo
qualunque traiettoria chiusa e’ nullo.
S. Moretto [email protected]
39
Energia Potenziale S. Moretto [email protected]
40
Forza Peso
In particolare ...
S. Moretto [email protected]
41
Energia potenziale gravitazionale
A
z
x
Lavoro compiuto
da/contro la forza peso
• nella caduta da A a B
• nel sollevamento da B a A
La forza e lo spostamento sono paralleli
hA
p = mg
suolo
B
h = hA–hB
hB
F = mg || s=h=hA-hB
L = mg•(hA-hB)
Dipende solo dall’altezza h rispetto al suolo (coord.z), non dalle coord. orizzontali x e y
S. Moretto [email protected]
42
Energia potenziale gravitazionale
Energia potenziale gravitazionale:
U = mgh = mghA­mghB
Dipende solo dall’altezza h rispetto al suolo (coord.z), non dalle coord. orizzontali x e y
L’energia potenziale e’ relativa a un punto di riferimento arbitrario (dipende dal “dislivello” tra due punti, non dall’altezza assoluta)
S. Moretto [email protected]
43
Forze Conservative e Dissipative
Forze Conservtive:
In questo caso il corpo “immagazzina” il lavoro
sotto forma di energia potenziale, riutilizzabile per compiere altro lavoro.
Se invece il lavoro dipende dal cammino seguito,
viene perduto sotto forma di energia non riutilizzabile (es. energia termica –calore­ negli attriti) e la forza e’ detta dissipativa. S. Moretto [email protected]
44
Energia Totale Meccanica
S. Moretto [email protected]
45
Teorema di Conservazione dell’Energia Meccanica
S. Moretto [email protected]
46
Conservazione dell’energia meccanica
Energia meccanica = energia cinetica T + energia potenziale U
In generale, in un campo di forze conservative:
L = T = TB-TA
TB-TA = UA–UB
TA+UA = TB+UB
L = UA–UB
CONSERVAZIONE DELL’ENERGIA MECCANICA
In un campo di forze conservative
(es.moto senza attriti sotto l’azione della forza peso),
la somma dell’energia cinetica e potenziale rimane costante.
S. Moretto [email protected]
47
Problema
S. Moretto [email protected]
48
Lavoro: Esempi
S. Moretto [email protected]
49
Potenza
S. Moretto [email protected]
50
Esercizi di cinematica
S. Moretto [email protected]
51
Esercizi
Es.1
Una palla è lanciata verso l’alto con velocità inziale
di 19.6 ms-1 da un’altezza iniziale di 2 m.
Calcolare:
1. quanto tempo impiega la palla per
raggiungere il punto piu’ alto della sua
traiettoria?
2. a che altezza dal suolo si trova tale punto?
v = v0 – gt
-> t= v0/g= 2 s
y = y0 + v0t – 1/2gt2
->y=21.6 m
v2 = v02 – 2g(y – y0)
S. Moretto [email protected]
52
Esercizi
Es. 2
Una forza orizzontale costante Fadi 150 N è applicata ad un
blocco di massa 60 Kg che è inizialmente fermo su di una
superficie senza attriti.
a) Dopo 3 s qual è la sua velocità?
b) Qual è la distanza raggiunta?
Fa
S. Moretto [email protected]
53
Esercizi
Fr
Fa
Fg
Seconda legge di Newton F = ma
->
a = F/m=2.5 m/s2
v = v0 + at
->
v = 7.5 m/s
x= x0 + v0t + ½ a t2
->
x = 11.25 m
Moto uniformemente accelerato:
x0=0
v0=0
S. Moretto [email protected]
54
Esercizi
Es. 3
Un blocco di 5 Kg sta scendendo da uno scivolo senza
attrito, di inclinazione 45o.
a) Qual è la sua accelerazione?
45o
S. Moretto [email protected]
55
Esercizio
Fr
Fg x
45o
Seconda legge di Newton F = ma
Fgy
Fg
->
a = Fgx / m
Fgx = Fg sin45
S. Moretto [email protected]
56
1. Una macchina ha una velocita` vi=70km/h quando inizia a
frenare e dopo 90m la velocita` si è ridotta a vf= 40km/h. Si
chiede di calcolare
l’accelerazione che supponiamo contante nella fase di
frenata.
a=[(vf)2-(vi)2]/2s=[(40/3.6)2-(70/3.6)2 ]/2*90= -1.4m/s2
il tempo di frenata
vf=vi+at da cui t= (vf-vi )/a =[(40/3.6)-(70/3.6)]/(-1.4)=5.9s
il tempo necessario affinche` la macchina si fermi
stessa formula t= (0-vi )/a =[0-(70/3.6)]/(-1.4)=14s
distanza percorsa in 12s
x-x0=vit+1/2 at2 =(70/3.6)*12 +1/2*(-1.41)*122=1.3*102m
S. Moretto [email protected]
57
Un proiettile è lanciato a 30o rispetto all’orizzontale . Si osserva
una gittata di 600m. Calcolare la velocita` iniziale del proiettile.
(trascurare la resistenza dell’aria)
R=2vo2sincos/g da cui vo=√(R*g/sin(2q)=82.4m/s
Un treno parte da Padova in direzione Milano, mantenendo una
velocita` costante di 120km/h. Calcolare dopo quanto tempo
incrocera` un treno che viaggia in direzione opposta, partito da
Milano nello stesso istante e che viaggia alla velocita` costante di
80km/h. Assumere la distanza Mi-Pd pari a 230km,
x1=x1o+v1ot
x1o=0 e v1o=+120km/h
x2=x2o+|vo2t
x2o=230 e vo2=-80km/h
x1=x2 ossia 120t=230-80t da cui t=1.15ore=1h 9minuti
S. Moretto [email protected]
58
Da una doccia sgocciola l’acqua cadendo sul fondo posto
2.00m più in basso . Le gocce cadono ad intervalli regolari: la
quarta goccia si stacca nell’istante in cui la prima arriva al
suolo. Trovare le posizioni della seconda e della terza goccia in
questo istante.
y=yo-1/2gt2 y=yo-1/2g(t-to)2
Dati due vettori a=3.0i+3.0j+3.0k e b=2.0i+1.0j+3.0k si
determini l’angolo compreso
axbx+ayby+azbz=abcosa=(ax2+ay2+az2)1/2
cosda cuicosossia =(25.8)o…..
S. Moretto [email protected]
59
Un uomo deve attraversare un fiume largo l=0.8km.Punta
la barca verso la riva opposta e rema con una velocita`
v=3.2km/h rispetto all’acqua. La corrente ha una
velocita` di 6.4km/h.
Quanto tempo impiega l’uomo ad attraversare il fiume?
In quale punto della riva opposta approdera` ?
vx=6.4km/h
(0,0)
(1.6,0.8)
vy=3.2km/h y-yo=vyt da cui
t=0.8/3.2=1/4 h
vx=6.4km/h x-xo=vxt=1.6km
vy=3.2km/h y-yo=vyt=0.8km
S. Moretto [email protected]
60
Esercizi sulle forze
S. Moretto [email protected]
61
Un motore trascina una massa m=150kg su un piano inclinato liscio
che forma un angolo =30o con l’orizzontale. La massa sale con
velocita`costante. Calcolare la forza esercitata dal motore
Ftot=0 Fmotore=mgsin=735N
mg
Un corpo scivola lungo un piano inclinato di 15o con velocita` costante.
Calcolare il coefficiente d’attrito fra il corpo e il blocco.
Fr=N=(mgcos) poiché la velocita` è costante
Fr=mgsine quindi =sin15/cos15=0.27
S. Moretto [email protected]
62
Esercizi:
1. Due blocchi da 10N sono collegati con una corda e appoggiano su una
superficie. Il coefficiente di attrito statico s=0.6. Calcolare:
•
la forza minima Fa necessaria per muovere il sistema
•
la tensione sulla corda di collegamento nel momento in cui il corpo
comincia a muoversi
B
T
A
Fa
1. Un blocco da 10N poggia su un piano inclinato (come sotto) ed è fermo.
Calcolare:
•
le forze di contatto e di attrito che agiscono sul blocco
•
il minimo valore del coefficiente di attrito tra il blocco e il piano
affinché il blocco stia fermo
250
S. Moretto [email protected]
63
Un corpo di massa m=60kg è soggetto, oltre alla forza peso ad
una forza verticale di 450N orientata verso l’alto. Calcolare
l’accelerazione del corpo.
Ftot=Fa+P Ftot=ma e quindi a=(450-mg)/m=-2.3m/s2
Un uomo di 70kg , sospeso ad un paracadute, scende con
un’accelerazione a=1.6m/s2. Calcolare la tensione del cavo che
sostiene l’uomo.
Ftot=T+P Ftot=ma e quindi T=Ftot -P=-70*1.6+70*9.8=574N
S. Moretto [email protected]
64
25o
50o
T3
T2
Determinare le tensioni delle
tre corde
T1
M =10kg
S. Moretto [email protected]
65
Esercizi Vari
S. Moretto [email protected]
66
Esempio
1-Un aereo a velocità costante v=350km/h rispetto al terreno, sgancia un pacco.
Trascurando la resistenza dell’aria:
a- Quali sono le componenti orizzontale (vxo) e verticale (vyo)della sua velocità
iniziale [vxo=350km/h, vyo=0]
b- Qual’é la componente orizzontale della velocità subito prima dell’impatto al
suolo? [vx= vxo=350km/h]
c- Se la velocità dell’aereo fosse stata maggiore (es.450km/h) il tempo di caduta
sarebbe stato maggiore minore od uguale? [uguale]
S. Moretto [email protected]
67
Esempio
2- In figura sono rappresentate 3 traiettorie di un pallone
Si chiede di metterle in ordine crescente
di:
a-durata del volo
b- Vyo,
c- Vxo,
d- Vo
3- una palla rotola orizzontalmente su un tavolo di altezza h=1.2m e cade al suolo ad una
distanza di 1.5m dal bordo. a-Per quanto tempo è stata in aria la palla [0.49s]
b-Qual’era la sua velocità prima di lasciare il tavolo[3.06m/s]
S. Moretto [email protected]
68
Esempio
4- Un proiettile è sparato con un angolo = 35o rispetto all’orizzontale e velocità
Vo=630m/s. Trascurando l’effetto dell’aria:
a- calcolare a quale distanza cade.[38.05km]
b- quanto tempo sta in
aria. [73.7s]
c- l’altezza massima raggiunta[6.67km]
5- Un proiettile è sparato con velocità Vo=150m/s. Sapendo che la sua gittata è 1500
m. Quanto vale l’angolo con cui è stato sparato [=(20.4)o, (69.6)o]
6- Un elettrone ha velocità iniziale v=106m/s orizzontale. Quanto si abbassa se deve
percorrere una distanza di 200m [s=1\2gt2 con t=0.0002s y=1.96.10-7≈0.2m]
S. Moretto [email protected]
69
Esempio
7 [RGM]La corrente di un fiume ha la velocità di 50 cm/s. Una persona nuota contro
corrente per 1km, quindi torna al punto di partenza; la sua velocità misurata
rispetto alla terra ferma in assenza di corrente risulterebbe 1.2m/s.
(a) Quanto tempo si richiede perché l’intero percorso, in andata e
ritorno venga compiuto?[33’ 37”]
(b) Quanto tempo si
impiegherebbe sull’intero percorso in assenza di corrente?[27’ 47”]
8 [RGM] Il pilota di un aereo vuole volare in direzione Est con il vento che soffia a
50km in direzione Nord . Se la velocità propria dell’aereo, cioè la velocità che il
velivolo ha rispetto al suolo quando vola in una direzione qualsiasi in assenza di
vento, è di 200km/h, (a) in quale direzione il pilota dovrà puntare l’aereo e (b)
quale sarà la velocità effettiva del velivolo rispetto al suolo in direzione Est.
[direzione Sud-Est 14.5o con la direzione Est; velocità effettiva verso Est
194km/h]
S. Moretto [email protected]
70
9[RGM] Una imbarcazione attraversa un fiume volgendo costantemente la prua in
direzione perpendicolare alle rive. La velocità propria del natante, cioè la velocità
che esso avrebbe rispetto alla terra ferma in assenza di corrente è di 2.0m/s; la
corrente parallela alle rive ha velocità di 1.0m/s. (a) Qual’è in modulo direzione e
verso la velocità risultante dell’imbarcazione? [2.23m/s]
(b) Se il fiume è largo 120m , in quanto tempo si compie la traversata? [60s]
(c) In quale direzione dovrebbe volgere la
prua per attraversare il fiume in direzione perpendicolare alle rive? [120o con la
direzione orientata della corrente]
10 [HRW] Siamo all’incrocio di due strade ortogonali tra loro. Un’auto della polizia P
viaggia a 80km/h lungo la strada X. L’automobilista M si sta avvicinando con
velocità di 60km/h lungo la strada Y . Qual’è la velocità dell’automobilista M
rispetto all’auto della polizia P?
11 [HRW] La neve sta cadendo verticalmente a una velocità costante di 8m/s . A quale
angolo rispetto alla verticale sembrano cadere i fiocchi di neve per il guidatore di
un’auto che viaggia a 50km/h?
S. Moretto [email protected]
71
Le Leve
solo se c’è tempo
Le leve
S. Moretto [email protected]
73
Tipi di leva
S. Moretto [email protected]
74
Leve
In base al tipo di leva si può avere:
un vantaggio statico, quando impiegando una minore potenza si può vincere una maggiore resistenza, ma per una distanza e una velocità inferiori. Un vantaggio statico provoca automaticamente uno svantaggio dinamico.
uno svantaggio statico, quando impiegando una maggiore potenza si può vincere una minore resistenza, ma per una distanza e una velocità superiori. Uno svantaggio statico provoca automaticamente un vantaggio dinamico.
un pareggio statico, cioè impiegando una uguale potenza si può vincere una uguale resistenza per una distanza e una velocità uguali. Un pareggio statico provoca automaticamente anche un pareggio dinamico.
S. Moretto [email protected]
75
Tipi di leve: Primo Tipo
Leva di primo tipo: nella leva di primo tipo il fulcro si trova tra la potenza e la resistenza. E' una leva che può dar luogo ad un vantaggio, ad uno svantaggio o ad un pareggio statico, a seconda che il braccio della potenza fosse più lungo, più corto o uguale al braccio della resistenza. E' una leva che si riscontra nel corpo umano anche se non troppo frequentemente.
Es. l'estensione dell'avambraccio sul braccio ad opera del
tricipite ­ il fulcro è dato dall'articolazione del gomito, la
potenza è data dall'inserzione del tricipite sull'olecrano e
la resistenza è data dal peso dell'avambraccio)
S. Moretto [email protected]
76
Tipi di leve: Secondo Tipo
Leva di secondo tipo: nella leva di secondo tipo la resistenza si trova tra il fulcro e la potenza. E' una leva che da sempre luogo ad un vantaggio statico. E' una leva che si riscontra molto raramente nel corpo umano.
Es. la flessione plantare del piede del piede da ritti ­ il
fulcro è dato dai metatarsi, la resistenza è data
dall'articolazione della caviglia e la potenza è data dal
muscolo tricipite surale sul calcagno
S. Moretto [email protected]
77
Tipi di leve: Terzo Tipo
Leva di terzo tipo: nella leva di terzo tipo la potenza si trova tra il fulcro e la resistenza. E' una leva che da sempre luogo ad uno svantaggio statico. E' una leva molto frequente nel corpo umano.
Es. la flessione dell'avambraccio sul braccio ad opera del brachiale ­ il fulcro è dato dal gomito, la potenza è data dall'inserzione del muscolo brachiale sull'ulna, la resistenza è data dal peso dell'avambraccio.
S. Moretto [email protected]
78
Le leve del corpo umano
Nel nostro corpo tutte le articolazioni, ossia le regioni di 'snodo'
tra le parti fisse, realizzano delle leve: quando sono in condizioni
di equilibrio consentono il blocco dell'articolazione, in caso
contrario ne consentono il movimento.
I Muscoli e le Leve
I muscoli scheletrici (che rappresentano l'elemento attivo del
movimento), inserendosi sulle ossa (che rappresentano l'elemento
passivo del movimento), per mezzo della contrazione muscolare
determinano il movimento. Questo è possibile grazie anche alle
articolazioni (che rappresentano l'elemento di congiunzione e perno
delle ossa).
Tutto l'apparato locomotore è basato su un sistema di leve. Questa
situazione determina che, tutte le volte che c'è movimento, si produce
una leva che può essere di primo, di secondo o di terzo tipo. Il fulcro
della leva è dato dall'asse di rotazione (di solito l'articolazione, ma può
anche essere un punto di appoggio o di presa); la potenza è data dal
punto in cui viene applicata la forza (di solito l'origine o l'inserzione
muscolare, non il ventre muscolare); la resistenza è data dal punto in
cui viene generata la resistenza stessa (un peso, lo spostamento di un
segmento corporeo, la gravità, ecc.).
S. Moretto [email protected]
79
Esempio:
Il caso dell'articolazione di appoggio della testa è un esempio di leva del primo tipo. Per bilanciare il peso del capo, applicato nel suo baricentro, ed evitare che la testa ciondoli in avanti, viene esercitata una potenza da parte dei muscoli nucali, che si trovano dall'altro lato rispetto al fulcro. L'intensità della forza realizzata dal muscolo sarà tale da produrre un momento esattamente uguale a quello prodotto dalla resistenza. Si noti anche che l'insieme delle due forze tenderebbe a causare un abbassamento del sistema: il fulcro realizza anche una reazione vincolare che si oppone alla traslazione: per questo dopo un certo tempo l'articolazione è affaticata!
S. Moretto [email protected]
80
Leve del corpo umano
S. Moretto [email protected]
81
Leve del corpo umano
S. Moretto [email protected]
82
Leve del corpo umano
S. Moretto [email protected]
83
Forza d’attrito
Forza d’attrito: forza che una superficie esercita su
un corpo a contatto con essa
Forza di contatto
alla superficie
Forza d’attrito
alla superficie
N
Fapp
Fr
p
L’attrito è una forza che si oppone sempre al moto
Il blocco non si muove finché Fapp non supera un’altra forza
s
che si oppone (Fr) mFd¹m
app =- F r
Se Fapp supera un certo valore (sN)
allora Fr non riesce più ad equilibrarla
e il blocco si mette in moto
Nel caso di un corpo in movimento
S. Moretto [email protected]
F r ≤m s N
F r @ md N
s coefficiente di attrito
statico ( dipende dal tipo di
superfici a contatto)
m d m s
rappresenta il
coefficiente di attrito
dinamico
84
Le forze di attrito nei fluidi: forze viscose e generalmente molto piccole
rispetto all’attrito tra superfici solide
Quando si cammina le giunture delle gambe sono ben lubrificate dal
fluido sinoviale che spremuto attraverso la cartilagine riveste le
giunture, questo lubrificante tende ad essere assorbito quando la
giuntura è ferma aumentando l’attrito e facilitando la posizione
fissa.
S. Moretto [email protected]
85
Da tener presente:
1.
Abbiamo indicato la forza d’attrito agente sul corpo che si trova al di
sopra della superficie di contatto ma anche per l’attrito vale il Terzo
Principio della Dinamica e quindi una forza uguale e contraria a quella
finqui` indicata agisce sulla superficie di contatto
2.
La forza d’attrito è sempre contraria al moto relativo dei due corpi a
contatto (può essere concorde al moto di uno dei due corpi in un altro
sistema di riferimento)
3.
L’attrito può trascinare un corpo; l’aderenza tra le superfici a
contatto frena il movimento dei solidi ma d’altra parte permette al
solido “passivo” di essere trascinato dal solido “motore”.
4.
In un solido che rotola il verso delle forze d’attrito statico non è
definito una volta per tutte ma dipende dalle condizioni di
sollecitazione. Ad esempio se un’automobile viene messa in moto dal
motore la forza d’attrito statico sulle ruote motrici ha verso opposto
a quello che avrebbe se l’automobile in panne, fosse spinta da dietro
da una persona
S. Moretto [email protected]
86
La bilancia misura il nostro peso?
a) Fermi sulla bilancia la forza peso W è uguale ed opposta alla forza
di reazione esercitata dalla bilancia e la risultante sulla persona è una
forza nulla
b) La forza di reazione è dovuta alla pressione dei piedi sulla bilancia
mentre il peso è dovuto alla gravità; R’=-R è ciò che indica la bilancia
c) La persona piega le ginocchia e le lascia accelerare verso il basso
così che la forza di reazione è ridotta R<W (la bilancia segnera’ un
valore più basso)
d) Quando si estendono le ginocchia esse premono i piedi più
fortemente sulla bilancia e la forza di reazione R>W (la bilancia
segnerà un valore più alto)
S. Moretto [email protected]
87