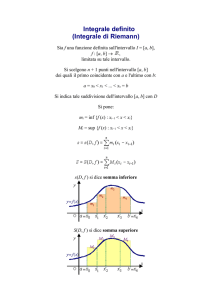
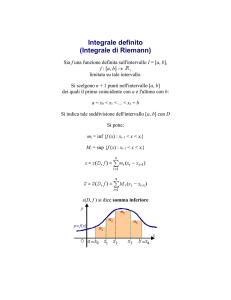
Corso di Laurea in Ingegneria delle Telecomunicazioni - A.A.2001-2002
Traccia del corso di Analisi Matematica L-B
1. Integrali impropri (o generalizzati)
Riferimenti. Barozzi: PCAM, par.5.8; Minnaja: Matematica Due, par.1.1
http://eulero.ing.unibo.it/~barozzi/SCAM/SCAM-tr01.pdf
1. Sia f : [a, +∞) → R una funzione integrabile su ogni intervallo [a, b]; diremo che essa è integrabile su
[a, +∞) se esiste finito il limite
b
lim
f (x) dx,
b→+∞
a
e si pone
+∞
f (x) dx := lim
b→+∞
a
b
f (x) dx.
a
Se f è integrabile su [a, +∞) si dice anche che l’integrale
Esempio 1.1. Per ogni λ > 0 si ha
b
1
1
e−λx dx = (1 − e−λb ) → ,
λ
λ
0
al contrario
b
1
dx = ln b → +∞,
x
1
+∞
a
f (x) dx è convergente.
per b → +∞;
per b → +∞.
Dunque x → e−λx è integrabile su [0, +∞), x → 1/x non è integrabile su [1, +∞).
In modo analogo, se f : (−∞, b] → R è una funzione integrabile su ogni intervallo [a, b], si pone
b
b
f (x) dx := lim
f (x) dx,
a→−∞
−∞
a
sempre che il limite indicato esista finito.
Se poi f : R → R, ed f è integrabile su ogni intervallo compatto, si pone si pone
∞
0
+∞
f (x) dx :=
f (x) dx +
f (x) dx,
−∞
−∞
0
a patto che entrambi gli integrali a secondo membro siano convergenti.
Esempio 1.2. Si ha
∞
e−|x| dx = 2,
−∞
in virtù di quanto visto nell’esempio precedente.
2. Sia f : (a, b] → R una funzione integrabile su ogni intervallo [c, b] con a < c < b; supponiamo che f non
sia prolungabile con continuità nel punto a (in tal caso il prolungamento di f è integrabile su [a, b] senza
problemi); ad esempio f può essere divergente per x → a+ . Diremo che f è integrabile su [a, b] se esiste
finito il limite
b
lim
f (x) dx,
+
c→a
c
e si pone
b
a
f (x) dx := lim+
c→a
b
f (x) dx.
c
1
Consideriazioni analoghe se f : [a, b) → R una funzione integrabile su ogni intervallo [a, c] con a < c < b,
essendo eventualmente divergente per x → b− .
√
Esempio 2.1. Per la funzione f (x) = 1/ x si ha, per ogni c ∈ (0, 1),
1
c
√
1
√ dx = 2(1 − c) → 2,
x
per c → 0+ ;
al contrario
1
c
1
dx = − ln c → +∞,
x
per c → 0+ .
√
Dunque x → 1/ x è integrabile su [0, 1], x → 1/x non è integrabile su [0, 1].
Esempio 2.2. Si ha, per ogni c ∈ (0, 1),
1
ln x dx = −1 − c ln c + c,
c
dunque la funzione logaritmo è integrabile sull’intervallo [0, 1] con integrale uguale a −1.
3. È interessante studiare l’integrabilità delle funzioni del tipo x → 1/xα , con α > 0, sugli intervalli [0, 1] e
[1, +∞). Abbiamo appena visto che per α = 1 gli integrali considerati sono entrambi divergenti. Tenendo
presente che una primitiva della funzione x → 1/xα = x−α si scrive
x →
1
x1−α ,
1−α
si trova
1
1
dx = +∞,
0 xα
α>1
=⇒
1
1
1
dx =
,
α
1−α
0 x
0<α<1
+∞
1
1
1
;
dx =
α
x
α−1
5
α=1
3
2
1
0
1
1
dx = +∞
x
+∞
1
dx = +∞
x
1
1
2
3
1
Le tre figure seguenti illustrano le diverse situazioni.
4
=⇒
4
5
2
+∞
1
dx = +∞.
xα
5
α>1
4
3
+∞
2
1
1
0
1
1
dx =
xα
α−1
1
1
dx = +∞
xα
1
2
3
5
4
5
0<α<1
4
3
2
0
1
1
1
dx =
xα
1−α
1
+∞
1
dx = +∞
xα
1
1
2
3
5
4
4. Teorema di confronto. Si ha la
Proposizione. Siano f, g : [a, +∞) → R due funzioni non negative, e si abbia ∀x, f (x) ≤ g(x). Allora
+∞
+∞
f (x) dx ≤
g(x) dx
a
a
nel senso che se l’integrale a secondo membro converge, anche l’integrale a primo membro converge, se
quest’ultimo diverge, anche l’integrale a secondo membro diverge.
x
x
Dimostrazione. Per le funzioni crescenti x → a f (t) dt e x → a g(t) dt si ha
x
x
∀x ≥ a,
f (t) dt ≤
g(t) dt,
a
a
dunque se g è integrabile su [a, +∞) tale è anche f , se f non è integrabile sullo stesso intervallo, tale è anche
g.
Esempio 4.1. La funzione pari x → e−x è integrabile su R. Infatti essa è integrabile su [−1, 1], in quanto
continua, ed è integrabile su (−∞, −1] e su [1, +∞) in quanto maggiorata da e−|x| .
2
1
e−x
2
e−|x|
-1
1
Grafico (non monometrico) delle funzioni f (x) = e−x , g(x) = e−|x| .
2
3
Osservazione. La funzione x → e−x (funzione gaussiana) non è integrabile elementarmente, nel senso
che non è possibile esprimere una sua primitiva come funzione composta mediante funzioni elementari. Con
varie tecniche è possibile dimostrare che
∞
√
2
2
e−x dx =
e−x dx = π.
2
R
−∞
La funzione appena considerata gioca un ruolo importante in Calcolo delle Probabilità nella forma
2
1
f (x) := √ e−x /2 ,
2π
(densità della distribuzione normale N (0, 1), con media 0 e deviazione standard 1), il cui integrale su R vale
1. Trattandosi di una funzione pari, l’integrale di f su ciascuno degli intervalli (−∞, −1] e su [1, +∞) vale
1/2. La primitiva di f che vale 1/2 per x = 0 (e dunque tende a 0 per x → −∞) si indica abitualmente
x
x
2
1
1
1
−t2 /2
Φ(x) := √
e
dt = + √
e−t /2 dt.
2
2π −∞
2π 0
Φ(x)
1
0.5
-4
-2
2
1
√ e−x /2
2π
2
4
Grafico (non monometrico) della distribuzione cumulativa Φ (= funzione di ripartizione) e della densità f
della distribuzione normale N (0, 1).
+∞
+∞
Corollario. Se f ∼ g, per x → ∞, allora gli integrali a f (x) dx e a g(x) dx o sono entrambi convergenti
o sono entrambi divergenti.
Esempio 4.2. La funzione f (x) := 1/(x2 + x + 1) è integrabile su R in quanto f (x) ∼ 1/x2 , per x → ±∞.
Esempio 4.3. L’integralseno
La funzione x → (sin x)/x è prolungabile con continuità per x = 0, attribuendole il valore 1; dunque la stessa
funzione è integrabile su ogni intervallo [0, a]. Studiamo l’integrabilità sull’intervallo [a, +∞). Poiché
sin x 1
x ≤ x,
il criterio del confronto non è direttamente applicabile. Tuttavia un’integrazione per parti fornisce
b
b
cos x
1
cos a cos b
sin x dx =
dx.
−
−
x
a
b
x2
a
a
Per b → +∞, (cos b)/b tende a 0, mentre il secondo integrale è convergente in quanto |(cos x)/x2 | ≤ 1/x2 .
Dunque x → (sin x)/x è integrabile su [0, +∞); con tecniche di variabile complessa mostreremo (Analisi
Matematica L-C) che
+∞
sin x
π
dx = ,
x
2
0
mentre
+∞
| sin x|
dx = +∞,
x
0
dunque f non è assolutamente integrabile (sinonimo: sommabile) su [0, +∞).
x La figura seguente (non in
scala monometrica) mostra a tratto continuo il grafico della funzione x → 0 (sin t)/t dt, nota anche come
seno integrale (o integralseno), e in tratteggio la funzione integranda:
4
π/2
1
π
10
5
15
20
Se la funzione x → | sin x|/x fosse integrabile sull’intervallo [0, +∞), si avrebbe
+∞
nπ
| sin x|
| sin x|
dx =
dx;
x
x
0
(n−1)π
n≥1
ma l’ultima serie scritta è divergente in quanto
nπ
nπ
| sin x|
| sin x|
2
dx ≥
dx =
,
x
nπ
nπ
(n−1)π
(n−1)π
e la serie che ha come termine n-esimo 2/(nπ) è divergente.
5. Teorema di confronto con gli integrali
Proposizione.
Se f : [1, +∞) è una funzione positiva e decrescente, allora l’integrale
n≥1 f (n) sono entrambi convergenti oppure entrambi divergenti.
+∞
1
f (x) dx e la serie
Dimostrazione → Minnaja p.26.
Esempio 5.1. La serie armonica generalizzata
Consideriamo la serie
1
, α > 0.
nα
n≥1
Sappiamo che essa è divergente per α = 1; a più forte ragione sarà divergente per 0 < α < 1, in quanto,
per tali valori di α, si ha 1/nα ≥ 1/n. Per α > 1 la serie in esame converge, in virtù della Proposizione
dimostrata, in quanto la funzione 1/xα è integrabile sull’intervallo [1, +∞).
5