Applicazione del Teorema di Thevenin mediante i grafici
I.T.I.S. Archimede Catania
delle caratteristiche esterne dei generatori reali, indipendenti e lineari.
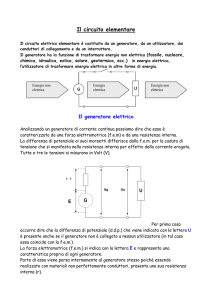
Consideriamo il circuito elettrico di Fig.1, che è relativamente semplice da risolvere. Ci proponiamo
di usarlo per fornire una applicazione del teorema di Thevenin, sfruttando le caratteristiche esterne
dei generatori reali di tensione, che nel caso di comportamento lineare non sono altro che delle rette.
La rete elettrica è costituita da due generatori di f.e.m. reali e lineari, collegati in parallelo rispetto ai
nodi A e B dai quali viene vista la rete. Secondo il suddetto teorema, la rete può essere ridotta ad
un generatore reale equivalente di tensione i cui valori sono definiti nel modo seguente: la f.e.m. ha
come valore la d.d.p. che si misura a vuoto tra i due nodi A e B, mentre la resistenza equivalente è
quella che si misura sempre tra gli stessi punti, però con le f.e.m. disattivate, cioè con la rete resa
passiva. Questi risultati trovano riscontro anche nei grafici di Fig.2..
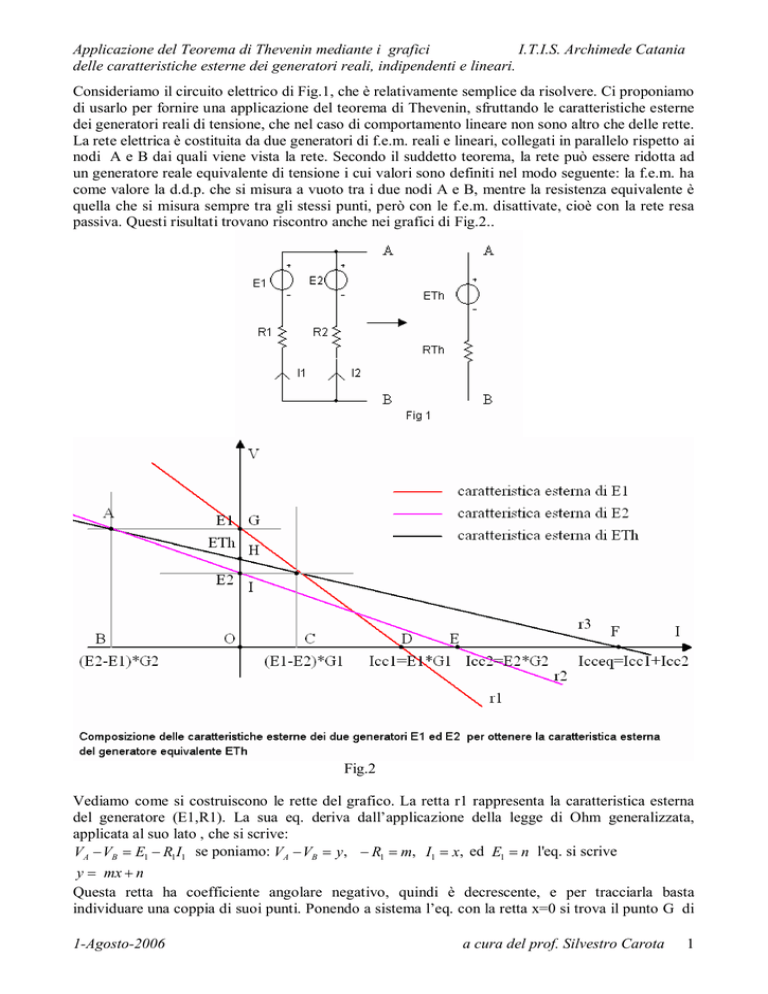
Fig.2
Vediamo come si costruiscono le rette del grafico. La retta r1 rappresenta la caratteristica esterna
del generatore (E1,R1). La sua eq. deriva dall’applicazione della legge di Ohm generalizzata,
applicata al suo lato , che si scrive:
VA − VB = E1 − R1I1 se poniamo: VA − VB = y, − R1 = m, I1 = x, ed E1 = n l'eq. si scrive
y = mx + n
Questa retta ha coefficiente angolare negativo, quindi è decrescente, e per tracciarla basta
individuare una coppia di suoi punti. Ponendo a sistema l’eq. con la retta x=0 si trova il punto G di
1-Agosto-2006
a cura del prof. Silvestro Carota
1
Applicazione del Teorema di Thevenin mediante i grafici
I.T.I.S. Archimede Catania
delle caratteristiche esterne dei generatori reali, indipendenti e lineari.
ordinata y=E1 e che corrisponde al termine noto. Ponendo a sistema l’eq. con la retta y=0 si trova il
punto D di ascissa x=Icc1, con I cc1 = E1G1 , che corrisponde alla corrente di c.c.. Unendo questa
coppia di punti con il righello si ottiene la caratteristica esterna del primo generatore; cioè la legge
che esprime la d.d.p. ai morsetti del generatore in funzione della corrente erogata o assorbita..
Ripetendo il procedimento per il secondo generatore si traccia la seconda caratteristica, che è data
dalla retta r2. La retta r3 corrisponde alla caratteristica del generatore equivalente, e può essere
costruita per via grafica seguendo questo ragionamento: i due generatori sono collegati in parallelo,
quindi hanno sempre in comune la d.d.p., ma al variare di questa la corrente che ciascuno di essi
eroga varia secondo la propria caratteristica esterna. Al nodo A convergono queste due correnti, che
per il P.P.K vanno sommate algebricamente. Sommare algebricamente queste correnti equivale a
sommare due ascisse, per cui, se immaginiamo di applicare al circuito un generatore di f.e.m. ideale
di valore opportuno, possiamo trovare per via grafica le due correnti. Conviene scegliere: una f.e.m.
nulla di eq. V=0 che coincide con l’asse delle correnti: Questa retta interseca le due caratteristiche
nei punti D ed E, in corrispondenza delle due correnti di c.c.: Quindi dal nodo A fuoriesce una
corrente pari alla somma I cceq = I cc1 + I cc 2 . Allora il primo punto cercato della caratteristica
equivalente è F ≡ ( I cc1 + I cc 2 , 0 ) . Per il secondo punto scegliamo un generatore ideale di f.e.m. pari
ad E1. Questo comporta il fatto che il generatore E1 non eroga corrente (ci troviamo nel punto G) e
V = E1
ciò si può ricavare dalla risoluzione del sistema
⇒ E1 = E1 − R1I1 ⇒ I1 = 0
V = E1 − R1I1
Mentre il generatore E2, in base a quest’altro sistema, eroga la corrente I 2 = −
E1 − E2
<0
R2
V = E1
E − E1
⇒ E1 = E2 − R2 I 2 ⇒ I 2 = 2
<0
R2
V = E2 − R2 I 2
E − E1
Allora il punto cercato è A ≡ 2
, E1 . Unendo con il righello i punti ottenuti A ed F si
R2
costruisce graficamente la caratteristica del generatore equivalente, e cioè la retta r3. Questa retta
interseca l’asse x nel punto F, mentre interseca l‘asse y nel punto H che è compreso tra i due punti
G ed I che corrispondono alle f.e.m. dei due generatori. In altri termini, se le due f.e.m. sono
concordi, la f.e.m. equivalente è compresa tra la maggiore e la minore delle due. Dalla formula che
scriveremo si capirà che tale f.e.m. è ottenuta da una media pesata delle due f.e.m. date, dove il peso
è legato alle rispettive conduttanze. Determinando l’ascissa del punto F e l’ordinata del punto H,
troveremo la f.e.m. e la resistenza del generatore equivalente secondo Thevenin. Così come
abbiamo fatto per i due generatori assegnati, punti D ed E, scrivendo I cc1 = E1G1 ed I cc 2 = E2G2 ,
possiamo scrivere per il generatore equivalente:
I cceq = I cc1 + I cc 2 = E1G1 + E2G2 ed usando i valori che stiamo cercando, possiamo scrivere
I cceq = EThGTh . Quindi: EThGTh = E1G1 + E2G2 Da questa relazione, una volta calcolato il valore
ETh
E1G1 + E2G2
Fissiamo ora la nostra attenzione sul grafico di Fig.2, per determinare l’ordinata del punto H, e cioè
il valore cercato ETh.
Prendiamo in considerazione i due triangoli rettangoli ABF e HOF. Essi sono simili perché
entrambi rettangoli e con l’angolo acuto di base in comune, (quello che insiste nel vertice F).
Essendo simili tali triangoli, possiamo immediatamente impostare la seguente relazione di
proporzionalità tra i loro lati corrispondenti : AB : HO = BF : OF .
di ETh siamo in grado di ricavare RTh : RTh =
1-Agosto-2006
a cura del prof. Silvestro Carota
2
Applicazione del Teorema di Thevenin mediante i grafici
I.T.I.S. Archimede Catania
delle caratteristiche esterne dei generatori reali, indipendenti e lineari.
Ma:
AB = E1 , HO = ETh , BF = I cceq − ( E2 − E1 ) G2 = E1G1 + E2G2 − ( E2 − E1 ) G2 =
= E1G1 + E2G2 − E2G2 + E1G2 = E1G1 +E1G2 = E1 ( G1 +G2 ) ,
OF = E1G1 + E2G2
Esplicitando l’incognita HO dalla precedente proporzione e sostituendo i valori sopra trovati si
AB × OF E1 × ( E1G1 + E2G2 ) ( E1G1 + E2G2 )
=
=
= ETh
scrive: HO =
E1 ( G1 +G2 )
BF
( G1 +G2 )
Questo risultato è quello che avremmo ottenuto se avessimo applicato direttamente il metodo di
Millman alla rete da ridurre. Resta da determinare la resistenza equivalente RTh , e per far questo
ETh
sfruttiamo la precedente relazione RTh =
ponendola a sistema con quella che dà il
E1G1 + E2G2
valore di ETh ottenuto:
ETh
( E1G1 + E2G2 )
RTh = E G + E G
( G1 +G2 )
1 1
2 2
1
1
R ×R
⇒ RTh =
=
=
= 1 2
1 1
E1G1 + E2G2
G1 +G2
R1 +R2
( E1G1 + E2G2 ) = E
+
Th
R1 R2
( G1 +G2 )
Quindi la resistenza equivalente è data dal parallelo delle resistenze dei due generatori.
1-Agosto-2006
a cura del prof. Silvestro Carota
3