# CONNESSIONE DI SISTEMI #
Riferimenti:
A.Ferrante, A.Lepschy, U.Viaro; “Introduzione ai controlli automatici.” UTET
Torino, 2000. ⇒ CAP. 3
A.Giua, C.Seatzu; “Analisi dei sistemi dinamici.” Springer, 2006.. ⇒ CAP. 7.2
• EFFETTI DI CARICO.
⇒
a)
• SCHEMI A BLOCCHI.
⇒
b)
• GRAFI DI FLUSSO DI SEGNALE (CENNI).
⇒
c)
• ALGEBRA DEGLI SCHEMI A BLOCCHI.
⇒
d)
a) Ipotesi:
¾ sistemi complessi lineari e stazionari costituiti tramite connessione
di sottosistemi (lineari e stazionari);
¾ trascurabilita’ degli effetti di carico.
⇒
esempio rete elettrica.
Secondo le ipotesi adottate, il sistema complesso, formato collegando i
diversi sottosistemi, sara’ descritto da un modello matematico
composto da:
1. – le equazioni relative a ciascun sottosistema; queste sono in
generale equazioni differenziali (sottosistemi dinamici), ma in
alcuni casi possono esserci anche equazioni algebriche (sottosistemi
istantanei);
2. le equazioni che esprimono i vincoli topologici (dipendenti dalle
modalita’ di interconnessione dei sottosistemi); tali equazioni sono
in generale algebriche dato che esprimono legami istantanei fra
grandezze d’ingresso e di uscita di sottosistemi diversi.
1
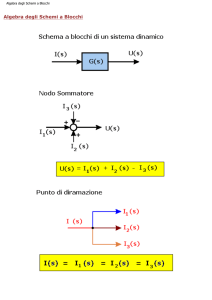
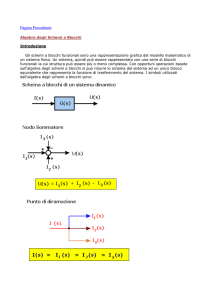
b) Rappresentazioni grafiche ⇒ Schemi a blocchi.
Uno schema a blocchi puo’ essere considerato come un insieme di
elementi dei seguenti tipi:
blocchi, usualmente rettangolari, che rappresentano una relazione
funzionale fra due grandezze (ingresso e uscita del blocco);
blocchi, usualmente circolari, che rappresentano la somma
algebrica di piu’ grandezze;
segmenti orientati, che rappresentano grandezze;
punti di diramazione, che corrispondono all’utilizzazione di una
stessa grandezza sotto aspetti diversi (per esempio come ingresso di
piu’ blocchi distinti o come uscita del sistema complessivo ma
contemporaneamente anche come ingresso di un suo blocco).
Con le ipotesi a) ai blocchi rettangolari si possono associare funzioni di
trasferimento (descrizione I.U.) ed e’ questo il motivo dell’uso molto
ampio degli schemi a blocchi per la descrizione e lo studio dei sistemi
⇒
di controllo nella teoria classica
x
+
e
C
_
r
u
Feedback Control
P
y
H
Schema standard di controllo a retroazione negativa
E’ opportuno accennare al fatto che l’impiego degli schemi a blocchi
puo’ essere esteso anche al caso di sistemi non lineari. Ad esempio, in
presenza di non linearita’ istantanee si associa al blocco la legge che
esprime il valore dell’uscita in funzione del valore assunto
dall’ingresso nello stesso istante.
2
Lo schema standard sopra riportato e’ di impiego assai diffuso e gioca
un ruolo fondamentale nella teoria classica del controllo. Con
riferimento a tale schema (a retroazione negativa o controreazione) si
definisce:
¾ x(t): ingresso,
y(t): uscita,
yd(t)=Kdx(t): uscita desiderata;
¾ e(t): errore, u(t): controllo, r(t): retroazione
¾ P(s): (f. di trasf. del) processo; C(s): (f. di trasf. del) controllore;
¾ H(s): (f. di trasf. del) trasduttore di retroazione;
¾ f. di trasf. della catena diretta la funzione: G(s)=C(s)P(s);
¾ f. di trasf. della catena di retroazione la funzione H(s);
¾ f. di trasf. di anello la funzione L(s)= − G(s)H(s);
¾ f. di trasf. di anello aperto la funzione F(s)= − L(s)= G(s)H(s);
¾ f. di trasf. a ciclo chiuso la funzione W(s)= G(s)/(1+F(s)).
La relazione tra W(s), G(s) ed F(s) e’ la relazione base della teoria
classica dei sistemi di controllo a controreazione e si ricava da:
Y(s) = X (s)G(s) − Y(s)F(s);
⇒
Y(s)[1 + F(s)] = X (s)G(s);
Y(s) G(s)
W(s) =
=
X (s) 1+ F(s)
3
c) Grafi di flusso di segnale (signal flow graphs).
Nei grafi di flusso ci si serve di nodi (punti o cerchietti) per
rappresentare i segnali e di archi o rami (segmenti di retta o archi di
curva, orientati) per rappresentare il legame fra il segnale d’ingresso e
quello di uscita di ciascun sottosistema.
Dato che nel seguito del corso adotteremo sempre gli schemi a blocchi
per lo studio dei sistemi di controllo di interesse, tralasciamo di
introdurre il formalismo dei grafi di flusso, di per se abbastanza
semplice da acquisire anche autonomamente.
c) Algebra degli schemi a blocchi.
L’algebra degli schemi a blocchi consiste sostanzialmente in una serie
di regole di manipolazione degli schemi che permettono di
trasformare lo schema di partenza in uno schema equivalente, piu’
comodo per l’utilizzo nel problema specifico. Tali artifici possono, in
effetti,
essere
considerati
come
l’equivalente
grafico
delle
manipolazioni da eseguire sulle equazioni del sistema per risolverle
(esprimere le uscite di interesse in funzione degli ingressi da cui
dipendono, eliminando le altre variabili).
Introdurremo le regole principali tramite la loro rappresentazione
grafica e le utilizzeremo per risolvere, a scopo esemplificativo, il
problema di determinare la funzione di trasferimento di un sistema
abbastanza complesso.
4