Capitolo
3
Fenomeni termici
1. Le scale di temperatura
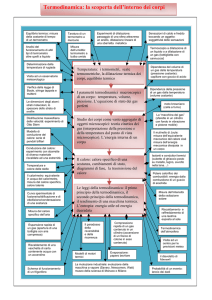
In che modo è possibile trasferire energia senza compiere del lavoro?
Alcune semplici osservazioni portano a concludere che esiste un complesso di
fenomeni, in cui viene trasferita energia, che non
possiamo descrivere
riconducendoli allo spostamento del punto di applicazione di una forza. Pensiamo
ad un veicolo che accelera nella direzione di marcia per l’azione di un motore a
vapore, aumentando così la sua energia cinetica. Consideriamo il veicolo nel suo
complesso come sistema. La legge di conservazione dell’energia permette senz’altro
di concludere che, visto che nessuna forza lavora dall’esterno, allora, a spese
dell’energia potenziale chimica del carburante, aumentano l’energia cinetica e, come
si osserva dal riscaldamento del veicolo, l’energia interna:
K U chim Eint 0
K Eint Uchim
Proviamo ora a cambiare la scelta del sistema, considerando il carburante un oggetto
esterno. Ricordiamo che per la conservazione dell’energia la variazione E deve
essere pari alla somma dei trasferimenti. Dobbiamo scrivere pertanto:
K Eint Trasferimenti
Ci rendiamo però conto di non disporre di uno strumento per quantificare questo
tipo di trasferimento energetico. Infatti si può certamente dire che i pistoni, tramite
le bielle, applicano una forza sulle ruote, compiendo del lavoro su di esse, e si può
anche dire che le molecole del vapore d’acqua in espansione nella caldaia esercitano
in qualche modo una forza sulle pareti dei pistoni. Ma queste sono tutte parti interne
al sistema. La sorgente esterna di trasferimento energetico è la fiamma che nasce
dalla combustione e riscalda l’acqua nella caldaia del motore. Non è possibile però
affermare che “la fiamma compie del lavoro sull’acqua” perché essa non esercita
alcuna forza sul sistema. E’ quindi necessario completare il quadro tramite
l’introduzione di nuove grandezze fisiche e nuove leggi che descrivano tali
fenomeni, che nel complesso diremo fenomeni termici.
TEMPERATURA
Proprietà dei corpi
FENOMENI
TERMICI
CALORE
Interazione fra i corpi
Quali grandezze ci occorrono per descrivere un fenomeno termico?
Una grandezza fisica non è qualcosa che “si scopre” ma piuttosto il risultato della
creatività umana che desidera costruire gli strumenti più adeguati per lo studio dei
fenomeni. Come in meccanica si introducono da un lato grandezze che descrivono
le proprietà dei corpi (massa ed energia), dall’altro grandezze che descrivono il
modo in cui i corpi interagiscono (forza e lavoro), ora per analogia cercheremo di
individuare due grandezze distinte nello stesso modo. La prima la diremo
temperatura, e vogliamo che esprima una proprietà termica degli oggetti, che
descriva cioè quegli stati fisici che non sono riconducibili a grandezze meccaniche.
La seconda la chiameremo calore e vogliamo che descriva quantitativamente
l’interazione fra i corpi per effetto delle loro proprietà termiche, cioè che descriva
quelle interazioni che non sono interpretabili come fenomeni meccanici.
La sensazione tattile di caldo descrivono una proprietà degli oggetti oppure un’ interazione?
Prima di dare delle definizioni operative di queste nuove grandezze, è
ragionevole chiedersi a quale delle categorie appartenga la più immediata fra le
esperienze che nel linguaggio colloquiale classifichiamo come sensazione di
calore. Ora, uno stesso corpo ci appare caldo se prima di toccarlo immergiamo
le mani in acqua fredda, e freddo se prima le immergiamo in acqua calda.
Questa semplice osservazione porta a concludere che quando usiamo i termini
caldo e freddo non stiamo descrivendo una proprietà dell’oggetto a contatto con
noi, altrimenti la sensazione di caldo/freddo non dovrebbe mutare visto che
l’oggetto non è stato alterato. Il tatto esprime piuttosto la relazione che corre
fra il nostro stato e quello dell’oggetto, e cioè un processo di interazione.
Quali difficoltà occorre superare per misurare lo stato termico dei corpi?
Per misurare la temperatura di un corpo abbiamo bisogno individuare una
qualunque proprietà fisica che vari con continuità al variare dello stato termico. Lo
stato termico viene quindi misurato per via indiretta, cioè attraverso indicatori degli
effetti che esso produce Esistono numerose proprietà che hanno queste
caratteristiche: a titolo di esempio citiamo il volume degli oggetti, la resistenza che le
sostanze offrono al passaggio di corrente elettrica, e tante altre ancora. Il problema è
che a seconda della proprietà alla quale si decide di fare riferimento, oppure della
sostanza che si sceglie di adoperare, la scala termica che si stabilisce è differente. Il
numero possibile di scale termometriche è quindi praticamente illimitato.
Su quali evidenze possiamo basarci per trasformare in una misura lo stato termico dei corpi?
DILATAZIONE DELLE SOSTANZE
Alle sensazioni di caldo e freddo è legata una variazione di volume delle
sostanze. La gran parte di esse si dilata al crescere della temperatura. E’ questo
l’effetto fisico che sfrutteremo come indicatore dello stato termico.
PRINCIPIO DELL’EQUILIBRIO TERMICO
In condizioni fisiche lontane da quelle del cambiamento di fase, il contatto fra
oggetti caldi e freddi tende a livellare i loro stati termici: quello caldo si
raffredda .e quello freddo si riscalda. Questo processo spontaneo si arresta
dopo un certo tempo, conducendo una situazione intermedia, nella quale cessa
ogni tipo di interazione. Lo stato raggiunto si dice
equilibrio termico.
L’enunciazione del principio dell’equilibrio termico si deve allo scienziato
2
scozzese Joseph Black (1728–1799) e fu scoperto relativamente tardi, nel XVIII
secolo, probabilmente perché contrasta con la semplice osservazione che
oggetti di materiale differente, come stoffe, metalli o legno appaiono
termicamente assai differenti al tatto anche quando si trovano alla stessa
temperatura.
PRINCIPIO ZERO DELLA TERMODINAMICA
L’equilibrio termico è transitivo: se A e C sono in equilibrio termico, e se B e C
sono in equilibrio termico, anche A e B sono in equilibrio termico. Questa
proprietà rende possibile il concetto stesso di misura garantendoci che quando
lo strumento B indica lo stesso stato termico per due oggetti A e C, possiamo
concludere che A e C sono in equilibrio termico anche se non li poniamo a
contatto.
TEMPERATURA DELLE TRANSIZIONI DI FASE
Esistono dei processi fisici che avvengono a valori fissi di temperatura, come le
transizioni dalla fase solida alla fase liquida di una sostanza pura, oppure il
processo di ebollizione alla pressione atmosferica. La stabilità di questi stati
termici ne rende possibile l’utilizzo come stati di riferimento.
Nella pratica, come costruire un indice dello stato termico di un corpo?
Lo strumento di misura, che diremo termometro, avrà caratteristiche diverse a
seconda dagli intervalli di temperatura che si desiderano misurare. Per valori
non troppo distanti dalle condizioni ambiente si individua innanzitutto una
sostanza che vari in modo facilmente misurabile il proprio volume
nell’intervallo di interesse. Per motivi che vedremo, la scelta cade sul mercurio
oppure sull’alcol od il toluolo, senza però dimenticare che, come si è detto, la
misura di temperatura che si ottiene sarà legata alle particolari proprietà ad
esempio del mercurio. L’effetto di dilatazione non sarebbe osservabile se non si
facesse uso di un meccanismo di amplificazione, consistente in un bulbo di vetro
alla base di un capillare. Il bulbo racchiude praticamente tutta la massa del
mercurio, e la parte di sostanza che trova posto nel capillare ne è solo una
porzione minima. In questo modo anche una piccola variazione di volume del
mercurio nel bulbo diventa assai evidente nel minuscolo capillare. Si scelgono
quindi due fenomeni fisici che individuino degli stati termici di riferimento, ad
esempio il congelamento e l’ebollizione dell’acqua alla pressione atmosferica. Si
misurano poi i valori assunti dalla grandezza scelta come indice dello stato
termico quando la sostanza è in equilibrio con quelle temperature: in questo
caso le lunghezze Xcong ed Xeboll della colonnina di mercurio. Un allungamento
corrispondente ad una temperatura compresa fra le due di riferimento avrà un
valore intermedio Xt . La frazione di allungamento rispetto a quello
corrispondente all’ebollizione, viene espressa su di una scala da zero a cento, si
fanno cioè cento suddivisioni uguali lungo la colonnina, e si continua a
graduare con lo stesso passo per misurare anche temperature sotto allo zero e
sopra ai cento. Il numero così ottenuto:
Xt Xcong
t
Xeboll Xcong
100 °C
3
CAPILLARE
X eboll
Xt
Xcong
BULBO
LA CONTROFISICA
La temperatura Celsius non è una
grandezza fisica perché il fatto che
due valori siano l’uno il doppio
dell’altro dipende dalla scelta dello
zero, che è del tutto arbitraria. Queste
stesse temperature non sono più,
infatti, più l’una il doppio dell’altra se
passiamo ad esempio alla scala
Fahrenheit.
è detto temperatura Celsius. Non si tratta di una misura nel senso in cui lo sono
le misure di lunghezza o di massa, perché avendo scelto arbitrariamente lo
zero non abbiamo stabilito cosa intendiamo per temperatura doppia o tripla, o
frazione di un’altra, ma solo cosa significa che un salto di temperatura è doppio
o triplo o frazione di un altro.
Il termometro clinico è uno strumento con queste caratteristiche?
Lo strumento che adoperiamo per vedere se abbiamo la febbre, detto
termometro clinico, differisce leggermente dalla descrizione fatta sopra, ed
appartiene ad una categoria detta termometri a massima. Fra il bulbo ed il
capillare è presente una strozzatura, foggiata in modo da permettere al
mercurio di uscire dal bulbo nella fase di riscaldamento. Non appena il liquido
comincia a contrarsi per il raffreddamento, la strozzatura produce la rottura
della colonnina, bloccando così la lettura sulla massima temperatura raggiunta.
Sono possibili altre scale con la stessa sostanza?
Nella scala Celsius l’ebollizione ed il congelamento dell’acqua valgono 100 °C e
0 °C , come si vede ponendo Xt Xeboll oppure Xt Xcong nella formula. I
valori assegnati agli stati di riferimento sono arbitrari, come arbitraria è la
suddivisione in cento parti dell’intervallo compreso fra essi. La scala Fahrenheit
assegna invece i valori 32 e 212 e divide in centoottanta parti, mentre per la
scala Kelvin le divisioni sono di nuovo cento ed i valori invece 273,15 e 373,15 .
CELSIUS
FAHRENHEIT
212
100
tC
0
KELVIN
373, 15
TK
tF
32
Ebollizione
dell’acqua
273, 15
Congelamento
dell’acqua
0
Rapportando la lunghezza della colonna di sostanza che si trova al di sopra
della temperatura di riferimento più bassa (rispettivamente tC , tF 32 e
TK 273,15 : si veda la figura) alla lunghezza dell’intervallo di temperature fra i
due riferimenti in ciascuna scala, abbiamo la formula di conversione:
tC
t 32 TK 273,15
F
100
180
100
4
Le unità di misura sono il grado Celsius °C, il grado Fahrenheit °F ed il kelvin K
(in questo caso la dicitura grado non si usa).
Che accade al momento in cui poniamo questo termometro a contatto con un oggetto?
Quando il termometro è a contatto con il corpo di cui vogliamo conoscere la
temperatura i due oggetti raggiungono l’equilibrio termico. Il volume raggiunto
dal liquido, su una scala tarata come sopra detto, è un effetto legato a questo
fenomeno e rappresenta un indice della temperatura di equilibrio termico. La
temperatura di equilibrio coincide con la temperatura dell’oggetto prima del
contatto (che è quella che vogliamo misurare) solo se possiamo considerare
trascurabile la perturbazione dovuta al termometro. Detto in altri termini, quella
che si misura è sempre la temperatura del termometro e non quella del corpo. Il
principio zero della termodinamica poi, ci assicura che quando il termometro
misura la stessa dilatazione del liquido per due corpi differenti, questi sono alla
stessa temperatura
Quali limiti presenta un termometro così concepito?
Vi sono innanzitutto limitazioni sull’intervallo di temperature di utilizzo, che non
può ovviamente estendersi oltre il campo di valori per i quali il liquido di misura si
congela (per il mercurio sono 39 °C ) oppure bolle ( 357 °C ). Non va poi
dimenticato che il procedimento di misura introduce una perturbazione. Un
termometro che si trovasse a temperatura molto maggiore di quella che si desidera
misurare cederebbe una considerevole energia all’oggetto, modificandone lo stato
termico e producendo una lettura priva di senso. Questo problema si fa sempre più
importante quanto più la temperatura da misurare si abbassa: vedremo nel seguito
la strategia che si adotta.
Le dilatazioni di sostanze diverse sono proporzionali fra loro?
Le dilatazioni della colonnina di mercurio sono ovviamente uniformi, per
definizione, rispetto ad una scala costruita tramite il mercurio. Vale a dire che
l’incremento di un grado corrisponde sempre alla stessa variazione di
lunghezza, indipendentemente dal fatto che avvenga fra 20 °C e 21 °C oppure
fra 60 °C e 61 °C , e questo semplicemente per il fatto che il termometro è stato
tarato proprio in modo da produrre un tale effetto. Ciò non è più vero se lungo
la scala del mercurio riportiamo le dilatazioni di una colonnina di alcol o di
toluolo, perché vi sono delle differenze fra le leggi di dilatazione delle sostanze.
Anche se abbiamo tarato gli indici di un termometro a toluolo ed uno a
mercurio in modo che segnino la stessa temperatura nelle posizioni di
riferimento, accadrà che ad esempio, quando il primo segna 50 °C , il secondo
segni una temperatura che in questa regione centrale può arrivare a differire
anche di 3 °C . Purché non si vada a temperature molto sotto lo zero o molto
sopra ai cento, dove il disaccordo supera le decine di gradi, da un punto di vista
pratico si tratta di scarti non eccessivi, e quindi possiamo senz’altro fare uso dei
termometri così costruiti. Concettualmente però questo ostacolo deve essere
superato, altrimenti non potremmo mai disporre di una misura di temperatura
che non sia legata alle particolari proprietà di dilatazione di questa o quella
sostanza.
5
Come è stato superato il problema del disaccordo fra i termometri?
Nella seconda metà del secolo XIX si osservò che, a differenza degli strumenti
che sfruttavano la dilatazione di sostanze allo stato liquido, i termometri a gas
mostravano un notevole accordo. Questa stabilità fra scale termometriche
costruite con gas differenti abbracciava ampi intervalli di temperatura, e
l’accordo fra le misure era tanto migliore quanto più rarefatti erano i gas di cui si
faceva uso. Gas come l’azoto, l’idrogeno, l’ossigeno e l’elio, quando vengono
riscaldati da 0 °C a 100 °C , mantenendone la pressione costante, aumentano di
oltre un terzo il loro volume: il fattore preciso varia da sostanza a sostanza. Ma
in condizioni di estrema rarefazione, quando la loro pressione tende ad
annullarsi (condizioni di gas ideale), il fattore di incremento fra il volume V100
del gas dilatato e quello V0 che possiede quando il bulbo è in equilibrio con il
ghiaccio fondente diviene per tutti uguale a:
V100 V0
100
0.36610
V0
273.15
Un semplice termometro a gas consta di un bulbo ed un cannello lungo cui
scorre una goccia e che sia aperto all’estremità per tenere la pressione
costantemente uguale a quella atmosferica. La suddivisione del cannello in
tacche uguali consente di legare la variazione di temperatura alla differenza
V100 V0 . Più in particolare, il valore del fattore di incremento del volume ci
dice che, essendo l’aumento V100 V0
di volume da 0 °C a 100 °C pari a
100
V0 , per ogni grado si ha un incremento pari a:
273.15
1
V0 V0
273.15
con
1
273.15
dove viene detto coefficiente di dilatazione termica, a pressione costante, dei
gas ideali. Il valore di temperatura letto dal termometro a gas ideale sarà allora
esprimibile da una formula che rapporti la variazione di volume complessiva
V V0 alla variazione V0 corrispondente ad una tacca della scala:
t
V V0
V0
La procedura consente quindi di ottenere una temperatura centigrada attraverso la
misura di un volume, misura che, se eseguita in condizioni di estrema rarefazione, è
indipendente dalla sostanza gassosa utilizzata.
Qual è la legge di dilatazione dei gas rarefatti a P costante?
Invertendo la formula che definisce la temperatura si ricava una legge di
dilatazione a pressione costante per i gas rarefatti, detta prima legge di GayLussac:
6
V
gas 1
V0
V V0 1 t
V0
V0
Esiste un limite inferiore alle temperature?
Si è soliti osservare che questa formula suggerisce un limite inferiore alle
temperature che possiamo immaginare di raggiungere. Infatti, se per ogni
1
grado di raffreddamento il volume del gas diminuisce di
V0 , qualora
273.15
scendessimo di 273.15 °C sotto alla temperatura di fusione del ghiaccio, il
volume del gas si annullerebbe. Non avrebbe allora senso pensare di scendere
a temperature più basse di 273.15 °C , perché secondo la prima legge di GayLussac queste renderebbero negativo il volume del gas. L’andamento lineare di
questa legge è raffigurato qui a fianco: la pendenza delle rette V0 dipende
solo dalla quantità di gas rarefatto presente (e quindi dal volume V0 che
occupa a t 0 °C ) ma non dal tipo di sostanza (cioè è una costante). L’idea
-273, 15 °C
gas 2
gas 3
0°C
t
LA CONTROFISICA
Non ha significato pensare a 273.15
sotto zero come la temperatura che il
gas avrebbe se non diventasse liquido,
perché il gas diventa liquido! Non
esiste un esperimento che possa
provare il raggiungimento di un
volume nullo da parte di un gas.
di un limite inferiore alle temperature nasce osservando che le rette incontrano
l’asse delle temperature in un unico punto:
V V0 1 t 0
t
1
273.15 °C
Tuttavia questo ragionamento, sebbene sia di guida all’intuizione, è privo di
supporto sperimentale perché presuppone l’esistenza, fino a temperature
estremamente basse, di un gas in condizioni ideali di estrema rarefazione, al
quale poter applicare la prima legge di Gay-Lussac. L’esperienza invece mostra
che, diminuendo progressivamente la temperatura di un aeriforme, si assiste
alla sua condensazione in liquido, per cui la sostanza cessa di esistere in quella
fase. Un successivo raffreddamento solidifica la sostanza, portandola ad
occupare uno spazio finito e ben determinato, per cui non vi è evidenza
sperimentale che autorizzi ad ipotizzare il raggiungimento di un volume nullo.
Quindi, il fatto che si trovi una intersezione matematica con l’asse delle
temperature prolungando, come nel tratteggio in figura, la retta della legge di
dilatazione dei gas rarefatti oltre la regione fisica di applicabilità, da solo non
basta per sostenere la presenza di un limite inferiore in corrispondenza di
t 273.15 °C . L’effettiva esistenza di un tale valore di zero assoluto per la
temperatura viene invece rigorosamente giustificata con altri argomenti, di
natura termodinamica, che saranno affrontati a suo tempo, e che consentono
anche di dimostrare che tutti i gas ideali definiscono la stessa scala.
Sulla base di questi risultati possiamo fissare una scala assoluta per la temperatura?
Il fisico britannico William Thomson (poi divenuto Lord Kelvin, 1824 –1907)
propose di adottare una scala centigrada assoluta di temperatura basandosi sulle
regolarità nel comportamento dei gas rarefatti, con uno zero proprio in
corrispondenza del valore 273.15 °C . Indicando con la maiuscola T la
temperatura assoluta, e con t i valori misurati per mezzo del termometro a gas
7
LA CONTROFISICA
E’ errato dire che allo zero assoluto le
molecole sono ferme. Per la loro
natura, le particelle elementari non
possono mai essere ferme. Se davvero
fossero ferme, conosceremmo con
esattezza il valore della loro velocità,
cioè zero, il che comporterebbe una
indeterminazione infinita sulla loro
posizione. E’ quanto afferma un
fondamentale principio di meccanica
delle particelle elementari dovuto ad
Heisemberg. Allo zero assoluto esse
sono invece in moto con il minimo
valore di energia cinetica che la loro
condizione permette.
rarefatto nella regione di applicabilità della prima legge di Gay-Lussac, con lo
zero invece in corrispondenza del ghiaccio fondente, si ha la semplice
relazione:
T
1
t 273.15 t
Invertendo la relazione, otteniamo anche una riformulazione semplice della prima
legge di Gay-Lussac nella scala Kelvin:
1 t T
V V0 T
Cosa significano dei valori di T fuori dalla regione misurabile con la legge di Gay-Lussac?
Per il momento i valori di temperatura fuori dalla regione in cui si può
applicare la legge di dilatazione dei gas rarefatti hanno solo un significato
matematico, e dovremo introdurre nel seguito un metodo che consenta di
definirli operativamente e misurarli. Di questo ci occuperemo studiando la
termodinamica, i cui strumenti consentiranno di dimostrare (1) che tutti i gas
ideali definiscono la stessa scala, (2) che esiste uno zero assoluto, temperatura
di un sistema che non può trasferire energia a nessun altro corpo che sia in
contatto con esso, (3) che è possibile una definizione operativa di temperature
fino a quel valore, (4) che la temperatura assoluta è una reale misura nel senso
in cui lo sono le misure di lunghezza o di massa, perché risulta legata al
contenuto energetico delle molecole e a differenza di quella basata sulla
dilatazione del mercurio, consente di stabilire cosa intendiamo per temperatura
doppia o tripla, o frazione di un’altra.
LA CONTROFISICA
E’ errato dire che si usa il termometro
a mercurio perché la sua scala è
lineare. Qualsiasi scala termometrica è
lineare, per definizione, rispetto alle
dilatazioni della sostanza che si è usato
per tararlo. Si tratti di alcol, toluolo,
mercurio od altro ancora, a qualunque
temperatura avvenga il salto di
un’unità, questo corrisponde sempre
alla stessa variazione di lunghezza
(diversa per ogni sostanza). Si usa il
mercurio principalmente per il suo
buon accordo con la scala assoluta.
Perché si fa comunemente uso del termometro a mercurio e non di quello a gas rarefatto?
Il termometro a gas è adeguato per un laboratorio scientifico, dove si eseguono
misure di grande precisione, ma risulta di poca utilità fuori da tale ambito a
causa della sua scarsa praticità. Uno strumento più agile, come quelli che
sfruttano la dilatazione dei liquidi, è senz’altro da preferire per l’uso
quotidiano, anche a scapito della precisione. La scelta del mercurio (o
dell’alcol) si deve al fatto che queste sono le sostanze che, nella regione fra 0 °C
e 100 °C , mostrano il migliore accordo con la scala assoluta.
2. Il trasferimento di energia per calore
La conoscenza della temperatura dei corpi esaurisce le informazioni sui fenomeni termici?
No: numerose osservazioni inducono a concludere che per descrivere i processi
termici la sola conoscenza della temperatura misurata con il termometro è
insufficiente. Si considerino ad esempio le esperienze seguenti:
8
1.
2.
3.
4.
Un certo quantitativo di acqua calda raggiunge l’equilibrio termico con
l’ambiente che lo circonda in tempi molto differenti a seconda che
l’acqua sia posta in un recipiente aperto, versata sul pavimento oppure
dentro ad un thermos chiuso. La temperatura finale di equilibrio è la
stessa nei tre casi, quindi il suo valore non ci dice nulla sui dettagli del
processo (ad esempio sul tempo impiegato).
Due quantitativi d’acqua differenti, uno grande ed uno piccolo,
inizialmente in equilibrio termico, quando sono riscaldati su due
fornelli identici, raggiungono un prefissato valore di temperatura in
tempi diversi, ed il quantitativo minore vi arriva molto prima. Anche
in questo caso la semplice informazione sulle temperature di partenza e
di arrivo, che sono le stesse, nasconde importanti dettagli.
Due sistemi posti in contatto raggiungono l’equilibrio termico con un
cambiamento di temperatura che non è lo stesso per entrambi, ma
dipende da vari fattori come la massa, la geometria, il tipo di sostanza
ecc., informazioni che non sono accessibili se si dispone solo della
temperatura di equilibrio raggiunta.
Un cubo di ghiaccio prossimo a 0°C , immerso in un grande
quantitativo di acqua calda, prima di raggiungere l’equilibrio termico
fonde mantenendo costante la propria temperatura. La conoscenza
della sola temperatura finale non contiene queste informazioni.
Quali informazioni occorrono per completare quella fornita dalla lettura del termometro?
Per descrivere i processi che comportano variazione di temperatura tramite il
contatto fra oggetti entreremo ora nel dettaglio della grandezza che abbiamo
chiamato calore. Vediamo in primo luogo come l’esperienza mostri due
importanti risultati: (1) che il contatto può anche non essere accompagnato da
variazioni di temperatura; (2) che il contatto non è l’unico fenomeno che
comporta una modifica della temperatura.
In quali modi può essere cambiata la temperatura di un corpo?
Abbiamo già considerato il principio dell’equilibrio termico, per il quale il
contatto fra due oggetti a differenti temperature (ma lontani dalla transizione
di fase), tende a modificare le temperature di entrambi. Non è questo tuttavia
l’unico meccanismo esistente; ricordiamo brevemente alcune esperienze:
1. L’attrito modifica la temperatura di un corpo: si consideri ad esempio lo
strofinio fra due superfici, oppure il riscaldamento del metallo quando
viene battuto o lavorato.
2. La presenza di corrente elettrica riscalda, anche considerevolmente, il
conduttore: il filamento di tungsteno di una comune lampada ad
incandescenza ad esempio supera i 2000 °C .
3.
4.
5.
Alcune reazioni chimiche possono essere accompagnate da variazioni
di temperatura dei reagenti.
La compressione di un gas tende a produrre un innalzamento della sua
temperatura: si pensi all’aria nel pistone di una pompa da bicicletta.
L’interazione con la radiazione può cambiare la temperatura. Si pensi
ad un oggetto lasciato al Sole ma anche al cibo nel forno a microonde.
9
Il contatto fra oggetti a temperature diverse è sempre accompagnato da variazione di T ?
Se il contatto avviene in corrispondenza di quel particolari condizioni fisiche
caratteristiche della transizione di fase di uno dei due, la sua temperatura
rimane costante.
Alla pressione atmosferica, mentre un ferro rovente
appoggiato sul giaccio si raffredda, il ghiaccio, raggiunti gli 0 °C , inizia il
processo di fusione mantenendo la temperatura inalterata.
Il contatto è accompagnato dal passaggio di qualche tipo di sostanza fra i corpi?
L’idea erronea dello spostamento fra i corpi di una sostanza detta “fluido
calorico” è stata invocata in passato a spiegazione del meccanismo di
livellamento delle temperature che il contatto comporta. Se quest’ipotesi fosse
vera però, dal riscaldamento prodotto per attrito su di un corpo, ad esempio
dalla punta di un trapano, si libererebbe una quantità potenzialmente
inesauribile di fluido calorico. La conclusione che tutto questo “fluido calorico”
era prima contenuto nel corpo appare paradossale e quindi l’ipostesi viene
respinta.
A quali meccanismi microscopici è riconducibile la temperatura?
Su scala microscopica ogni corpo è costituito da un enorme numero di
particelle, che a seconda della sostanza potranno essere atomi, oppure ioni,
molecole od anche aggregati di milioni di molecole. Nella fase solida queste
particelle sono vincolate a delle posizioni determinate nello spazio, attorno alle
quali possono oscillare; nelle fasi liquida ed aeriforme hanno invece libertà di
movimento in qualunque direzione. Quale che sia lo stato di aggregazione,
molte esperienze indicano che tali particelle non sono ferme, ma risultano
animate di moto caotico. Pur essendo assente uno spostamento ordinato
d’insieme, ognuna di loro si muove con propria velocità e direzione,
indipendentemente da quello che fanno le altre. Nel caso dei solidi si tratta di
vibrazioni attorno ad una posizione di equilibrio, nel caso di liquidi e gas si
tratta di liberi spostamenti in tutte le direzioni, sovrapposti a rotazioni. Quello
che chiamiamo “temperatura di un oggetto” è semplicemente il modo in cui si
manifesta al tatto, o durante il contatto con altri oggetti, il moto di agitazione
caotica che su scala microscopica anima le sue particelle. La nostra definizione
di temperatura basata sul dilatamento delle sostanze non fa riferimento a tutto
questo, ma come vedremo più avanti è possibile introdurre una scala di
temperatura legata allo stato di agitazione delle particelle. Il risultato di questi
studi mostra come la temperatura può essere ricondotta all’energia cinetica con
cui traslano le particelle:
LA TEMPERATURA DI UN OGGETTO È DIRETTAMENTE PROPORZIONALE AL VALORE MEDIO
DELL’ENERGIA CINETICA DOVUTA MOTO CAOTICO DI TRASLAZIONE DELLE PARTICELLE CHE
LO COSTITUISCONO :
T K traslazione delle particelle
Cosa accade, microscopicamente, durante il contatto fra sostanze a temperature differenti?
Nel contatto le molecole veloci del corpo caldo interagiscono, tramite urti, con
quelle lente del corpo freddo. In seguito alle collisioni le prime mediamente
rallentano, le seconde acquistano velocità. Questo scambio di energia cinetica
10
fra le molecole delle due sostanze tende a condurre i corpi stessi verso uno
stato di agitazione omogeneo, cioè ad una temperatura di equilibrio compresa
fra le due iniziali. Nel caso di corpi solidi le interazioni per il raggiungimento
dell’equilibrio partono dalla superficie di contatto e si propagano, se invece la
fase è liquida oppure aeriforme, gli scambi energetici sono agevolati dalla
possibilità per le sostanze di mescolarsi, che comporta una moltiplicazione delle
regioni di contatto.
IL RAGGIUNGIMENTO DELL’EQUILIBRIO TERMICO È QUINDI UNO SCAMBIO DI ENERGIA
CINETICA AL LIVELLO DEL MOTO DI AGITAZIONE MOLECOLARE
Il contatto fra due corpi a diversa temperatura è quindi un analogo del lavoro?
Si perché comporta un trasferimento di energia. Il corpo più freddo avrà, alla
fine del processo, variato l’energia cinetica media delle sue particelle
incrementandola per portarsi alla temperatura di equilibrio, viceversa per il
corpo inizialmente più caldo. Tuttavia, su scala macroscopica tale trasferimento
energetico non può essere ricondotto allo spostamento del punto di
applicazione di una forza, perché tutte le interazioni sono avvenuta alla scala
delle molecole. Sono le collisioni fra le molecole, dovute al moto disordinato di
agitazione termica, ad essere responsabili dello scambio di energia, ma il fatto
che stiamo osservando l’effetto di un fenomeno microscopico, in qualche modo
nasconde questa parte degli aspetti fisici. Per completare la descrizione del
fenomeno di trasferimento energetico si introduce, allora, la grandezza
termodinamica Q detta energia trasferita per calore, o più semplicemente calore.
Q rappresenta la quantità di energia che viene scambiata per effetto degli urti
fra le molecole dovuti al moto disordinato di agitazione termica. Analogamente
al lavoro, anche il calore descrive un trasferimento energetico, e precisamente
Q è l’energia trasferita unicamente per effetto della differenza di temperatura.
Q:
ENERGIA TRASFERITA PER VIA TERMICA, CIOÈ PER EFFETTO DEGLI URTI CHE
AVVENGONO FRA LE MOLECOLE DI SOSTANZE CHE SONO A TEMPERATURE DIFFERENTI
ATTRAVERSO LA SUPERFICIE CHE LE SEPARA
L: ENERGIA TRASFERITA PER VIA MECCANICA, CIOÈ PER EFFETTO DELLO SPOSTAMENTO
DEL PUNTO DI APPLICAZIONE DI UNA FORZA LUNGO LA DIREZIONE DELLA FORZA
Il calore non è quindi una sostanza, e nemmeno una proprietà dei corpi, come i
primi fisici che studiarono termologia furono indotti a pensare, ma piuttosto la
descrizione di un processo.
Quindi calore e lavoro sono due modalità di scambio energetico?
Si, in un certo senso è come se il sistema andasse a rifornirsi da un benzinaio che
dispone di due pompe differenti: calore e lavoro possono essere visti come due tipi
di carburante ugualmente in grado di riempire il serbatoio dell’energia di ogni
sistema. Il lavoro è l’energia scambiata con l’ambiente come risultato di modifiche
nella forma o nella configurazione del sistema. Esso si esprime tramite parametri
11
LA CONTROFISICA
Anche se in fisica si è soliti riferirsi a
Q come “calore” qui preferiamo
chiamarlo “energia trasferita per
calore” ad evidenziare che il calore
non è una sostanza, ma un processo di
trasferimento il cui oggetto è l’energia.
In questo modo è più facile evitare
l’errore di parlare di “calore contenuto
in un corpo”. Solo l’energia è
posseduta dai corpi: non si può stipare
del calore come non è possibile stipare
del lavoro. Q ed L esistono solamente
durante i processi di trasferimento e
non possono essere immagazzinati.
ENERGIA
Q
7 5
w
J
4 0
J
CALORE LAVORO
Q
macroscopici ed è dovuto all’azione di forze che spostano il loro punto di
applicazione, facendo così subire alle molecole del sistema una variazione nella
velocità del moto ordinato d’insieme. Il calore, invece, corrisponde all’energia
scambiata attraverso la superficie di separazione tramite le collisioni fra le molecole
del sistema e quelle dell’ambiente, quando fra questi esiste una differenza nella
temperatura (e quindi nell’energia media di agitazione molecolare). I cambiamenti
energetici coinvolti sono in questo caso al livello microscopico. Le particelle
guadagnano (o perdono) energia sotto forma di traslazioni, vibrazioni, rotazioni ecc,
subendo una variazione nella velocità del moto disordinato di agitazione termica.
w
12