Gli eroi della nostra storia

Calcolabilità
2012/2013
M.Di Ianni
Gli eroi della nostra storia
Da Time del 29 marzo 1999: “Nei moderni calcolatori confluiscono tante idee e tanti progressi tecnologici che sarebbe
temerario assegnare a una sola persona il merito di averli inventati. Ma rimane il fatto che chiunque batta su una tastiera
aprendo una tabella a doppia entrata, o un programma di videoscrittura, lavora su una incarnazione della macchina di
Turing”.
In questa dispensa, cerchiamo di ripercorrere alcune delle tappe principali del pensiero umano che hanno condotto alla
macchina Universale di Turing.
Torniamo, dunque, al sogno di Leibniz e a quello che, tale sogno ha ispirato ai logici del periodo che va dalla metà del
XVIII alla metà del XIX secolo.
Ricordiamo che Leibniz sognava l’esistenza di un linguaggio tanto potente da poter
a) rappresentare tutta la conoscenza umana
b) risolvere qualsiasi problema, posto su qualunque argomento, mediante l’applicazione meccanica delle regole
del linguaggio.
In realtà, il sogno di Leibniz ha radici molto antiche, molto anteriori alla sua nascita.
6.1
La logica di Aristotele
La Logica Aristotelica è raccolta in una serie di scritti dal titolo complessivo di Organon, ossia, in greco “Strumento”.
Comunque, i termini “logica” e “organon” sono posteriori. Il termine che Aristotele (383 a.c.) utilizza per designare
l’oggetto dei suoi studi è analitica, per indicare che si tratta di un metodo di risoluzione del ragionamento ai suoi
elementi costitutivi.
Organon è il nome dato da Andronico di Rodi (I sec. a.C.), seguace di Aristotele tra i Peripatetici, all’edizione standard
delle sue sei opere di logica. Secondo altre fonti, il termine Organon viene utilizzato per la prima volta da Alessandro
di Afrodisia (I sec. d.C.) e fu poi adottato dal VI d.C. per denominare il complesso degli scritti aristotelici. Comunque
sia, il termine “Organon” significa “strumento” e servirebbe a sottolineare la funzione propedeutica o introduttiva della
logica come strumento di cui si avvalgono tutte le scienze.
Il termine “logica” è quasi certamente di origine stoica, e possiamo intenderlo come scienza dei “logoi”, ossia, scienza
dei discorsi, riferendosi al suo oggetto di studio: il pensiero espresso nei discorsi.
Lo sviluppo della logica aristotelica va pensato in parallelo allo sviluppo della metafisica. In effetti, Aristotele non
inserisce la logica nel quadro delle scienze come scienza a sé stante. Piuttosto, Aristotele la intendeva come studio
della struttura della scienza in generale. Infatti, secondo Aristotele esiste un rapporto necessario fra le forme del
pensiero, studiate dalla logica, e le forme della realtà, studiate dalla metafisica. L’esistenza di questo rapporto è una
Calcolabilità, 2012/2013
Gli eroi della nostra storia
1
delle questioni più controverse che hanno occupato i matematici del periodo che ci accingiamo ad analizzare (XIX e
XX secolo).
Alla base della logica aristotelica è il concetto di proposizione: una affermazione che può avere uno solo di due valori,
vero oppure falso. Aristotele fondava la logica su tre principi:
- principio di identità: ogni proposizione è uguale a sé stessa;
- principio di non contraddizione: non possono essere contemporaneamente vere sia una proposizione che la sua
negazione;
- principio del terzo escluso: fra una proposizione e la sua negazione, almeno una di esse deve essere vera.
Osserviamo che sul principio del terzo escluso è basata la tecnica di dimostrazione per assurdo: poiché una affermazione genera una contraddizione allora essa deve essere falsa e, quindi, in virtù del principio del terzo ecluso la sua
negazione deve essere vera.
Il principio di non contraddizione è considerato da Aristotele il perno di ogni ragionamento, come è espresso nella sua
Metafisica: “È impossibile che la stessa qualità appartenga e non appartenga alla stessa cosa . . . Questo è il più certo
di tutti i principi . . . Per questa ragione tutti coloro che eseguono qualche dimostrazione si riferiscono ad esso come a
una conoscenza fondamentale. Esso è infatti, per natura, la fonte di tutti gli altri assiomi”1 .
Aristotele introdusse anche il ragionamento per sillogismo. Il sillogismo (dal greco syllogismòs, formato da syn,
“insieme”, e logismòs, “calcolo”: quindi, ragionamento concatenato) è un tipo di ragionamento dimostrativo che,
partendo dai tre tipi di termine giunge ad una conclusione collegando i suddetti termini attraverso brevi enunciati
(premesse). Il sillogisma più noto di Aristotele è il seguente:
Socrate è un uomo
(premessa maggiore)
Tutti gli uomini sono mortali
(premessa minore)
Allora, Socrate è mortale
(conclusione).
I termini di un sillogismo sono detti maggiore, che funge da predicato nella conclusione (nell’esempio, mortale),
medio (nell’esempio, uomo e uomini) e minore, che nella conclusione funge da soggetto (nell’esempio, Socrate); essi
vengono classificati in base al rapporto contenente - contenuto, e sulla base di tale classificazione, dalle premesse si
deriva la conclusione.
Le proposizioni che compongono un sillogismo categorico possono essere:
- universali affermative (“Tutti gli A sono B”),
- universali negative (“Nessun A è B”),
- particolari affermative (“Qualche A è B”),
- particolari negative (“Qualche A non è B”).
Il sillogismo non è altro che una regola di inferenza. Nella logica matematica, una regola di inferenza è l’atto di trarre
una conclusione basandosi sulla forma delle premesse. Nel caso una regola di inferenza sia corretta allora stabilisce
quando un enunciato formalizzato (cioè, come si dirà molto più tardi, una formula di un linguaggio proposizionale
o del primo ordine) è conseguenza logica di un altro soltanto sulla base della struttura sintattica degli enunciati.
Possiamo, allora, considerare il sillogismo come il primo passo verso l’automatizzazione dei processi deduttivi, ossia,
verso ciò che oggi chiamiamo calcolabilità.
Il sillogismo che abbiamo descritto risponde alla regola di inferenza detta del modus ponens, che nel linguaggio
proposizionale viene espressa come
[ ( p → q ) wedge p ] ⇒ q,
1 Come riportato nel testo di Davies (Nota a fine dispensa), questo passo viene citato in G. Boole, An investigation of the Laws of Thought on
which are Founded the Mathematical Theories of Logic and Probabilities, 1854.
Calcolabilità, 2012/2013
Gli eroi della nostra storia
2
che va interpretata nel modo seguente: “se so che ogni volta che è vera p anche q è vera, e mi accorgo che, nel mio
caso particolare, p è vera, allora posso dedurre che, nel mio caso particolare, q è vera”2
Il modus tollens è una seconda regola di inferenza della logica proposizionale, sviluppata compiutamente per la prima
volta dai logici medievali ma conosciuta già agli stoici. Letteralmente, “modus tollens” possiamo tradurlo come: “il
modo che toglie la verità di una proposizione togliendo quella di un’altra”. Nel linguaggio proposizionale essa viene
espressa come
[ ( p → q ) wedge ¬q ] ⇒ ¬p,
che va interpretata nel modo seguente: “se so che ogni volta che è vera p anche q è vera, e mi accorgo che, nel mio
caso particolare, q è falsa, allora posso dedurre che, nel mio caso particolare, p è falsa”.
Osserviamo che, comunque, nella logica proposizionale l’unica regola di inferenza necessaria è il modus ponens.
Concludiamo questo paragrafo osservando che già per gli stoici (300 a.c.) la logica non è più solo uno strumento al
servizio della metafisica, ma acquista dignità di disciplina autonoma.
Per “logica” gli stoici intendevano non solo le regole formali del pensiero che si conformano correttamente al Logos,
ma anche i costrutti del linguaggio con cui i pensieri vengono espressi: Logos può significare sia ragione che discorso;
dunque, oggetto della logica sono i logoi, ossia i ragionamenti espressi in forma di proposizioni.
Questo punto di vista avrà immense conseguenze nel resto della nostra storia.
6.2
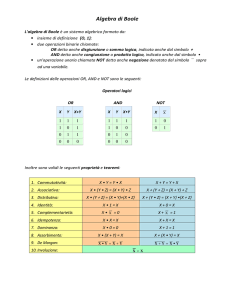
Boole e l’algebra della logica
L’interesse di George Boole (1815-1864) nella ricerca di un formalismo matematico in grado di produrre “automaticamente” la risposta a qualsiasi problema è di chiara ispirazione leibniziana ed è testimoniato fin dai suoi scritti
giovanili.
In Inghilterra, patria di Boole, si stava cominciando a capire che la potenza dell’algebra nasceva dal fatto che i simboli
scelti in rappresentanza di quantità e di operazioni ubbidivano ad un ristretto numero di regole. Come conseguenza di
ciò, gli stessi metodi dell’algebra erano applicabili a qualunque oggetto e operazione che ubbidissero alle stesse leggi.
Come abbiamo visto, a logica aristotelica (che era stato anche il punto di partenza di Leibniz) studiava i sillogismi, e
te forme del sillogismo includevano frasi del tipo: “tutti gli uomini sono mortali”, oppure “nessun uomo è una pianta”.
Boole comprese che, ai fini del ragionamento logico l’aspetto essenziale di parole come “uomo” o “pianta” era la classe
o collezione di tutte le individualità descritte dalla parola. Egli, inoltre, individuò un sistema per formulare questo tipo
di ragionamenti per mezzo di un’algebra delle classi: le classi venivano indicate come lettere (ad esempio, x) cosı̀
come già venivano utilizzate per rappresentare numeri nell’algebra ordinaria. Se x ed y rappresentavano due classi,
Boole indicava con xy la classe degli oggetti che stavano sia in x che in y3 : in qualche modo, Boole stava assimilando
questa nuova operazione fra classi alla moltiplicazione numerica. Sussisteva, però, una differenza sostanziale: se x è
la classe dei fiori rossi, allora xx è ancora la classe dei fiori rossi. Ossia, nella nuova algebra che stava nascendo era
sempre valida l’equazione
xx = x.
(6.1)
Questa osservazione indusse Boole a considerare la stessa equazione nell’algebra ordinaria: nell’algebra ordinaria
l’equazione xx = x è vera se e soltanto se x = 0 oppure x = 1. Dunque, l’algebra della logica coincide con l’algebra
ordinaria limitata ai due soli valori 0 e 1.
I due valori 0 e 1 andavano, quindi, interpretati come classi. Per capire, però, in che modo consideriamo le moltiplicazioni per 0 e per 1 nell’algebra ordinaria: qualunque sia il valore di x,
0·x = 0
1 · x = x.
Se interpretiamo le due identità sopra nel linguaggio delle classi, ese sono vere quando indichiamo con
• 0 la classe che non contiene alcunché, che oggi chiamiamo insieme vuoto,
• 1 la classe che contiene qualunque entità cui possiamo pensare, che potremmo chiamare universo.
2 Si
osservi l’utilizzo dei due diversi simboli di implicazione → (implicazione materiale) e ⇒ (implicazione logica).
classe viene chiamata, nella Teoria degli Insiemi, intersezione di x ed y, e l’operazione che la calcola viene indicata con il simbolo ∩.
3 Tale
Calcolabilità, 2012/2013
Gli eroi della nostra storia
3
Rimaneva ancora da interpretare, nella nuova algebra, l’altra operazione definita nell’algebra ordinaria: l’addizione.
Boole stabilı̀ che x + y rappresentava la classe contenente tutto ciò che è contenuto in x o in y4
Boole individuò nella sua algebra anche l’operazione inversa dell’addizione: x − y denota la classe contenente tutto
ciò che è contenuto in x ma non è contenuto in y. In particolare, 1 − x, la classe complemento di x, rappresenta tutto
ciò che non è contenuto in x. Allora,
x + (1 − x) = 1,
ossia, qualunque oggetto deve essere in una classe o nel suo complemento: una rilettura del principio del terzo escluso
di Aristotele.
Utilizziamo, ora, la notazione x2 per indicare xx e vediamo come possiamo interpretare la regola fondamentale di
Boole (6.1): tale regola può venire scritta come x2 = x da cui, applicando il primo principio di equivalenza delle
equazioni dell’algebra ordinaria, otteniamo x2 − x = 0. Possiamo, come nell’algebra ordinaria, raccogliere a fattor
comune e ottenere
x (1 − x) = 0,
ossia, niente può sia appartenere che non appartenere a una classe. Per Boole questo fu un risultato entusiasmante,
che rafforzò la sua convinzione di essere sulla strada giusta: infatti, questa equazione esprimeva proprio quel principio
di non contraddizione che Aristotele ha descritto come l’assioma fondamentale di tutta la filosofia.
6.3
Frege, la teoria degli insiemi e Russell
La teoria degli insiemi è stata introdotta nell’ambito degli studi dei fondamenti della matematica e può essere considerata parte della logica matematica.
Prima della metà del sec. XIX la nozione di insieme veniva considerata solo come qualcosa di intuitivo e generico.
La nascita della Teoria degli insiemi come branca della matematica viene generalmente fatta risalire alla pubblicazione, nel 1874, dell’articolo del matematico tedesco Georg Cantor (1845-1918) Über eine Eigenschaft des Inbegriffes
aller reellen algebraischen Zahlen (Su una proprietà della collezione dei numeri reali algebrici). Fra il 1879 e il
1884, Cantor pubblicò una serie di sei articoli nei Mathematische Annalen che, nel loro complesso, costituiscono una
introduzione alla sua teoria degli insiemi.
Il termine “insieme” è la parola chiave della matematica del XX secolo, proprio grazie al contributo di Cantor che ha
permesso di rifondare l’intera matematica sulla teoria degli insiemi. In effetti, si è passati, successivamente dalla teoria
ingenua di Gottlob Frege (1848-1925) alla teoria assiomatica di Zermelo-Fraenkel, attraverso un lungo travaglio che
ha modificato sensibilmente il modo di vedere la matematica.
Gottlob Frege (1848-1925), matematico e filosofo tedesco, uno dei più grandi logici del nostro tempo, è stato il
primo fautore del logicismo, ossia della prospettiva secondo la quale l’aritmetica, in quanto costituita da proposizioni
analitiche, sarebbe riducibile alla sola logica. In effetti, con la sua rivoluzionaria opera Begriffsschrift (difficilmente
traducibile, che possiamo rendere come Ideografia o Scrittura per concetti) del 1879 voleva aprire una nuova era
rifondando la matematica sulla logica. Oltre alla Ideografia, egli successivamente al suo progetto in Die Grundlagen
der Arithmetik (I Fondamenti dell’aritmetica) e in Grundgesetze der Arithmetik (I Principi dell’aritmetica): queste
opere rappresentarono appunto il tentativo di derivare esplicitamente le leggi dell’aritmetica da un sistema di assiomi
mediante un calcolo logico costituito da lunghe catene deduttive nelle quali, secondo Frege, non avrebbe dovuto
inserirsi nulla di intuitivo e di non deducibile logicamente. Dati i limiti del linguaggio naturale, sottolineati spesso in
modo critico dallo stesso Frege, al fine di realizzare questo progetto era necessario utilizzare un linguaggio formale
dotato di un suo proprio simbolismo, di un linguaggio in formule del pensiero puro a imitazione di quello aritmetico: è
appunto questo il linguaggio simbolico presentato nell’Ideografia. Si osservi come tali concetti riconducano al calculus
ratiocinator di Leibniz.
Abbiamo già visto che il concetto di insieme è un concetto primitivo. Intuitivamente, possiamo dire che un insieme è
un aggregato di oggetti che verificano tutti la proprietà caratteristica o legge di appartenenza ma che, in questo modo,
utilizziamo soltanto un sinonimo per la parola “insieme”.
La teoria ingenua degli insiemi di Frege si fonda sui due principi enunciati nel seguito.
4 Tale
classe viene chiamata, nella Teoria degli Insiemi, unione di x ed y, e l’operazione che la calcola viene indicata con il simbolo ∪.
Calcolabilità, 2012/2013
Gli eroi della nostra storia
4
1) Il principio di estensionalità: enunciato per la prima volta da Leibniz, afferma che due insiemi con gli stessi
elementi sono uguali.
2) Il principio di comprensione: afferma che ogni proprietà determina un insieme ed ogni insieme è determinato
da una proprietà.
L’obiettivo, ambizioso, di Frege era quello di fondare l’intera matematica su due principi cosı̀ semplici e logicamente elementari. Comunque, nel 1902 Bertrand Russell (1878-1932) scoprı̀ che il principio di comprensione era
contraddittorio.
La dimostrazione di Russell della contaddittorietà del principio di comprensione consiste, sostanzialmente, nell’esibizione di un controesempio. In generale, un controesempio relativo ad una affermazione è un esempio in cui
l’affermazione è non vera . In particolare, il controesempio al principio di consistenza proposto da Russell si basa
sulla seguente osservazione: un insieme può anche contenere sé stesso come oggetto. Ad esempio, l’insieme dei concetti astratti un concetto astratto e, dunque, l’insieme dei concetti astratti appartiene all’insieme dei concetti astratti.
D’altra parte, non tutti gli insiemi contengono sé stessi come oggetto: l’insieme dei fiori rossi non è un fiore rosso e,
dunque, l’insieme dei fiori rossi non appartiene all’insieme dei fiori rossi.
Sia, allora, A l’insieme degli insiemi che non contengono sé stessi come oggetto. La questione, ora, è decidere
A ∈ A?
Supponiamo che A ∈ A: allora A conterrebbe sé stesso come oggetto, dunque non potrebbe contenere A.
Allora, A non deve appartenere ad A; ma, in questo caso, A non contiene sé stesso come oggetto, e dunque A ∈ A.
Dunque, si giunge ad una contraddizione sia partendo dall’ipotesi A ∈ A che partendo dall’ipotesi A 6∈ A. In altri
termini, la proprietà “contiene sé stesso come oggetto” non determina un insieme, e il principio di comprensione viene
contraddetto.
Il paradosso (o, più propriamente, l’antinomia) di Russell minacciava la consistenza stessa della matematica. Numerosi tentativi furono tentati dallo stesso Russell e da gran parte dei logici che operarono nella prima metà del XX secolo
per superarlo. Nel tentativo di risolvere l’antinomia, in modo tale da conservare la validità dell’idea (alla base del
Logicismo) per cui la matematica può essere fondata completamente dalla logica, Russell sviluppò in collaborazione
con Alfred North Whitehead la teoria dei tipi, esposta nei tre monumentali volumi dei Principia Mathematica (pubblicati fra il 1910 e il 1913). Partendo dalla logica pura dell’Ideografia di Frege, utilizzando solo passi semplici e diretti
(aiutati dal sistema simbolico introdotto da Peano), gli Russell e Whitehead tentarono di evitare i paradossi grazie ad
una elaborata e pesante stratificazione in cui ogni insieme poteva avere solo elementi appartenenti ad uno stesso strato.
Tuttavia, questa struttura rendeva necessaria l’introduzione di un principio (di validità dubbia) che permettesse di attraversare le barriere fra strato e strato: l’assioma di riducibilità. Nonostante i loro punti deboli, comunque, i Principia
Mathematica rappresentano una pietra miliare nella storia dei fondamenti della matematica, perché dimostrarono la
fattibilità della formalizzazione completa della matematica all’interno di un sistema di logica simbolica.
La distinzione fra classi e insiemi e l’introduzione di nuovi assiomi ha portato, successivamente, al passaggio alla teoria
assiomatica degli insiemi. Fra i diversi sistemi assiomatici proposti, si sono assestati due sistemi di assiomi chiamati
rispettivamente sistema assiomatico di Zermelo-Fraenkel e sistema assiomatico di Von Neumann-Bernays-Gödel.
6.4
Hilbert e l’Entscheidungsproblem
Negli anni Venti del ventesimo secolo il matematico tedesco David Hilbert (1862-1943) lanciò una sfida che avrebbe
portato a risultati tanto sorprendenti quanto inattesi: fondare la matematica sulla matematica stessa, ossia, usare gli
stumenti messi a disposizione dalla matematica per convalidare la matematica stessa.
L’interesse di Hilbert per i fondamenti della matematica e, in particolare con il pensiero astratto, sono evidenti fin
dai suoi primi lavori. Nel 1897, con la pubblicazione dello Zahlbericht (Relazione sui numeri) Hilbert presentò una
risistemazione critica di tutto il settore della Teoria Algebrica dei Numeri (disciplina, peraltro, relativamente nuova)
a partire dai suoi principi fondanti. Nel 1898 tenne un corso di Elementi di Geometria Euclidea nel quale si propose
di fondare la geometria. Hilbert introdusse una assiomatizzazione della geometria che sottolineava la natura astratta
dell’argomento: si doveva dimostrare conla pura logica che i teoremi seguivano dagli assiomi, senza l’influenza di
Calcolabilità, 2012/2013
Gli eroi della nostra storia
5
quello che possiamo vedere osservando una figura. Stando a un famoso aneddoto, Hilbert avrebbe sostenuto che i
teoremi devono rimanere veri anche se parlano non di punti, rette e piani, ma di tavoli, sedie e boccali di birra, sempre
che questi oggetti obbediscano agli assiomi.
Hilbert dimostrò che i suoi assiomi erano coerenti, ossia non derivava da essi alcuna contraddizione: in realtà, ciò che
venne dimostrato da Hilbert era che ogni eventuale contraddizione del suo sistema di assiomi ne avrebbe determinanta
una anche nell’aritmetica dei numeri reali. In altri termini, aveva ridotto la coerenza della geometria euclidea a quella
dell’aritmetica, rimandando, di fatto, la prova della coerenza di quest’ultima.
Durante il Congresso Internazionale dei Matematici di Parigi del 1900, Hilbert presentò una relazione in cui propose
la sfida del Novecento: ventitré problemi che apparivano intrattatibili con i metodi esistenti. Il primo di tali problemi
era l’ipotesi del continuo di Cantor. Il secondo dei problemi posti da Hilbert era proprio la coerenza degli assiomi
dell’aritmetica dei numeri reali. Comunque, Hilbert iniziò ad affrontare sul serio il problema solo negli anni Venti
quando iniziò a coniderare il dualismo dentro al sistema / fuori dal sistema: ossia, introdusse un linguaggio simbolico
puramente formale nel quale sviluppare contemporaneamente matematica e logica e che aveva significati diversi se
visto dall’interno o dall’esterno. Visto dall’interno, non era che matematica, in cui ogni passo deduttivo era totalmente
esplicitato. Visto dall’esterno, invece, non era che un insieme di formule e manipolazioni di simboli che potevano
essere eseguite a prescindere dal loro significato. Hilbert si proponeva di dimostrare che in un tale linguaggio non era
possibile derivare due formule che contraddicessero in maniera esplicita.
In questo modo, Hilbert aveva steso un’importante linea di demarcazione fra il suo lavoro ed i contenuti dei Principia
Mathematica di Russell e Whitehead. In effetti, mentre Frege aveva compreso con chiarezza di avere a che fare con
due livelli linguistici (quello del sistema formale da lui costruito e quello del linguaggio ordinario nel quale si poteva
parlare di tale sistema), nei Principia Mathematica i due livelli venivano confusi: pertanto, il problema della coerenza
della struttura, cruciale per Hilbert, nei Principia Mathematica non si poneva nemmeno.
In un manuale di logica pubblicato (insieme ad Ackermann) nel 1928, Hilbert pose due problemi relativi alla logica di
base della Ideografia di Frege (quella che oggi chiamiamo logica del primo ordine):
1) dimostrare che la logica del primo ordine era completa, ossia, dimostrare che ogni formula che, vista dall’esterno, appariva valida poteva essere derivata dentro il sistema utilizzando solo le sue regole;
2) trovare un metodo che, data una formula della logica del primo ordine, determinasse in un numero finito di passi
ben definiti ed effettivi, se essa era o non era valida.
Il secondo di questi problemi è noto come l’Entscheidungsproblem (problema della decisione) e, come vedremo, fu lo
spunto di partenza che condusse alla Macchina Universale di Turing.
Durante il Congresso Internazionale dei Matematici di Bologna del 1928, Hilbert pose un problema che è una restrizione di quello descritto al punto 1) sopra. In particolare, Hilbert pose il problema della completezza dell’Aritmetica
di Peano (in breve, PA, illustrata nell’Appendice A della Dispensa 4), intendendo, con ciò, che di ogni proposizione
esprimibile in PA si potesse dimostrarne in PA la verità o la falsità. Poco dopo, un giovane logico avrebbe dato a
questo problema una soluzione del tutto inaspettata.
6.5
Gödel e il Teorema di Incompletezza
Abbiamo già incontrato Kurt Gödel (1906-1978) in relazione ai suoi studi sull’ipotesi del continuo di Cantor, e già
sappiamo come iniziò ad interessarsi ai fondamenti della matematica.
Una volta presa la direzione che lo conduceva verso i fondamenti della matematica e verso il lavoro di Cantor sull’infinito attuale, Gödel utilizzò la sua profonda inclinazione filosofica per porre domande di importanza essenziale: che
cosa è una dimostrazione? La dimostrazione di una proposizione coincide con la verità della proposizione stessa? Una
proposizione vera è sempre dimostrabile? Può un sistema limitato produrre la dimostrazione di qualcosa che va al di
là del sistema?
Nella sua tesi di dottorato, Gödel affrontò il primo dei problemi posti da Hilbert ed Ackermann: lo studio dell’eventualità che nell’insieme di regole deduttive dell’Ideografia di Frege incorporate nei Principia Mathematica esistessero
delle lacune, ossia, inferenze deduttive da una qualche ipotesi ad una qualche tesi che, viste dall’esterno, apparissero
Calcolabilità, 2012/2013
Gli eroi della nostra storia
6
corrette ma tali che le regole di Frege non permettevano di derivare la tesi dalle ipotesi. In altre parole, ciò che Hilbert
volva dimostrare era che
se un presunto teorema è tale che
ogni assegnazione di valori alle variabili in esso presenti che renda vera l’ipotesi rende vera anche
la tesi
allora il teorema è dimostrabile usando le regole di Frege-Russell.
La tesi di dottorato di Gödel con il suo Teorema di completezza (1929) dimostra quanto si proponeva Hilbert. Esso
stabilisce una corrispondenza tra la verità semantica di una asserzione e la sua dimostrabilità logica nella logica del
primo ordine.
Dopo aver dimostrato il Teorema di completezza, Gödel iniziò ad interessarsi al problema posto da Hilbert durante il
Congresso di Bologna del 1928, ossia, la verifica che di ogni proposizione esprimibile in PA si potesse dimostrarne
in PA la verità o la falsità. La prima cosa sulla quale Gödel cominciò a riflettere fu quello che poteva significare
considerare un sistema logico dall’esterno anziché dall’interno. Whitehead e Russell avevano mostrato che l’intera
matematica ordinaria poteva essere sviluppata dentro un sistema formale; di contro, Hilbert si proponeva di usare metodi matematici per studiare questi sitemi formali dal di fuori, definendo, di fatto, una sorta di metamatematica.
Gödel iniziò allora ad interrogarsi circa la possibilià di sviluppare la metamatematica stessa dentro un sistema formale.
Visti dall’interno, questi sistemi esprimono proposizioni a proposito di oggetti matematici, ma visti dall’esterno essi
appaiono come relazioni fra stringhe e simboli. Chiariamo questo concetto con un esempio: consideriamo la proposizione relativa al sistema PA “ogni numero naturale che abbia un predecessore è maggiore o unguale ad 1”. Possiamo
esprimere tale proposizione nella logica del primo ordine come
∀x [ ∃y : A(x, y) ⇒ F(x) ],
assegnando il significato opportuno ai simboli x, y, A e F. Vista dall’esterno, tale espressione non è altro che una
sequenza di simboli, che potremmo interpretare anche “chiunque ami è felice”.
A questo punto, Gödel individuò un procedimento per codificare le stringhe di simboli mediante numeri naturali: la
gödelizzazione, che abbiamo già incontrato. E si rese conto che con una tale codifica, l’esterno poteva essere portato
all’interno. In altri termini, Gödel si accorse che era possibile utilizzare i codici per costruire la metamatematica di un
sistema logico formale all’interno del sistema stesso.
Indichiamo con PM il sistema logico formale dei Principia Mathematica di Russell e Whitehead. Gödel riuscı̀ a
dimostrare che
la proprietà di un numero naturale di essere il codice di una proposizione dimostrabile in PM è essa
stessa esprimibile in PM.
Forte di questo risultato, Gödel riuscı̀ a costruire in PM proposizioni A che, conoscendo la codifica utilizzata, potevano
essere intrepretate come esprimenti il fatto che una certa proposizione B non era dimostrabile in PM. Gödel si chiese,
poi, se A e B, che generalmente sono proposizioni diverse, avrebbero potuto coincidere. In effetti, potevano coincidere,
e Gödel riuscı̀ a dimostrarlo utilizzando la tecnica della diagonalizzazione di Cantor.
Dunque, Gödel era riuscito ad ottenere una proposizione U cosı̀ strutturata
U = U non è dimostrabile in PM.
Supponiamo, ora, che tutto ciò che viene dimostrato in PM sia vero; allora, con la sequenza di passi illustrati di seguito,
arriviamo a dimostrare che U è vera ma non dimostrabile, né confutabile, in PM.
• U è vera. Supponiamo, infatti, che U sia falsa: allora, è falso che U non è dimostrabile in PM; quindi U è
dimostrabile in PM e dunque, poiché abbiamo supposto che tutto ciò che viene dimostrato in PM è vero, U deve
essere vera, contraddicendo l’ipotesi che sia falsa. Quindi, U è vera.
• U non è dimostrabile in PM. Poiché U è vera deve essere vero quello che afferma!
Calcolabilità, 2012/2013
Gli eroi della nostra storia
7
• La negazione di U, ¬U, non è dimostrabile in PM. Poiché U è vera, allora ¬U è falsa; ma poiché abbiamo
supposto che tutto ciò che viene dimostrato in PM è vero, allora ¬U non è dimostrabile in PM.
Per affermare che né U né la sua negazione ¬U sono dimostrabili in PM, si dice che U è indecidibile in PM. Ribadiamo
che, comunque, l’indecidibilità è soltanto interna a PM, mente, dall’esterno U è una proposizione vera.
Gödel riuscı̀ anche a dimostrare che: entro PM si può dimostrare
se PM è coerente, allora U.
(6.2)
Questo ha una conseguenza notevole. Poiché sappiamo che U non è dimostrabile in PM, allora la coerenza di PM
non può essere dimostrata in PM (altrimenti la dimostrazione della coerenza di PM unita alla dimostrazione di (6.2)
sarebbe una dimostrazione di U).
La pubblicazione nel 1931 di questi risultati nel lavoro Su alcune proposizioni indecidibili dei “Principia Mathematica” e di sistemi affini 5 fu preceduta da una presentazione informale degli stessi durante la “Conferenza sull’epistemologia delle scienze esatte” tenutasi a Königsberg nel 1930. Al termine della presentazione, ebbe luogo conversazione
fra Gödel e Von Neumann in cui Gödel chiarı̀ ulteriormente la questione della indimostrabilità della coerenza di PM.
La conclusione che Von Neumann ne trasse fu che questa era la fine del programma di Hilbert.
Si osservi, infine, come il Teorema di Completezza ed l Teorema di Incompletezza di Gödel potrebbero, ad una analisi
poco attenta, apparire contraddittori. In effetti, però, essi si riferiscono a due accezioni diverse del termine “completezza”: il Teorema di Completezza afferma che tutte le formule che sono conseguenza logica sel sistema formale di
Frege sono dimostrabili, mentre il Teorema di Incompletezza dimostra che alcune formule non sono dimostrabili né,
tantomeno, sono conseguenza logica di una certa teoria.
6.6
Da Leibniz alla Macchina Universale di Turing (attraverso l’Entscheidungsproblem)
Abbiamo già visto molto del lavoro di Turing nella logica e nell’informatica. Quello che ci proponiamo di fare, in
questo paragrafo, è inquadrare il suo lavoro all’interno del movimento intellettuale che ha animato i logici che hanno
operato fra la metà del XIX e la metà del XX secolo. Ripercorriamo, dunque, brevemente, i passi più significativi di
questo percorso.
Ricordiamo, allora, che il primo a sognare di ridurre i processi della mente umana a puro calcolo era stato Leibniz. Che,
sulla sua scia, Boole aveva progettato un sistema di calcolo che operasse, invece che sui numeri, sulle proposizioni.
Successivamente, Frege aveva prodotto un sistema di regole capace di riprodurre gli schemi deduttivi umani. Gödel,
nella sua tesi di dottorato, aveva dimostrato che le regole di Frege erano complete. Hilbert aveva provato ad andare
anche oltre la questione della completezza e della coerenza dei sistemi formali, ponendo l’Entscheidungsproblem: egli
cercava procedure di calcolo esplicite che, date alcune premesse ed una ipotetica conclusione, scritte nella notazione
della logica del primo ordine, permettessero sempre di stabilire se la seconda deriva dalle prime.
In effetti, il programma degli studi matematici consisteva (e consiste!) in buona parte di queste procedure, dette
anche algoritmi: a partire da quelle per eseguire le operazioni elementari (addizione, moltiplicazione, ecc.), a quelle
che permettono la risoluzione di espressioni algebriche, fino alle procedure che permettono il calcolo di integrali e
la soluzione di equazioni differenziali. Hilbert, tuttavia, cercava un algoritmo di una potenza senza precedenti che,
almeno in linea di principio, avrebbe dovuto ridurre tutti i ragionamenti deduttivi a puro calcolo: il sogno di Leibniz.
Alan Turing (1912-1954) venne in contatto con i problemi connessi ai Fondamenti della Matematica nel 1935, seguendo un corso tenuto da M.H.A. Newman, che a sua volta, ne era rimasto affascinato dopo aver ascoltato Hilbert durante
5 In realtà, il Teorema di Incompletezza di Gd̈el è molto più potente di quanto illustrato in questa dispensa. Esso prova che in ogni formalizzazione
coerente della matematica sufficientemente potente da assiomatizzare la teoria elementare dei numeri naturali è possibile costruire una proposizione
sintatticamente corretta che non può essere nd́imostrata né confutata all’interno dello stesso sistema.
Si osservi che l’esistenza di sistemi incompleti non è una scoperta particolarmente sorprendente - se si elimina il postulato delle parallele dalla
geometria euclidea si ottiene un sistema incompleto (nel senso che il sistema non dimostra tutte le proposizioni vere). L’essere incompleto per un
sistema formale significa semplicemente che esso non include tutti gli assiomi necessari a caratterizzare univocamente uno specifico modello.
Ciò che Gödel ha mostrato è che nella teoria dei numeri, nella teoria degli insiemi o nell’analisi matematica, in ogni sistema formale potente
come questi sistemi, non è mai possibile giungere a definire la lista completa degli assiomi che permetta di dimostrare tutte le verità: ogni volta che
si aggiunge un enunciato all’insieme degli assiomi, ci sarà sempre un altro enunciato non incluso.
Calcolabilità, 2012/2013
Gli eroi della nostra storia
8
il Congresso di Bologna del 1928. Il corso di Newman terminava con il Teorema di Incompletezza di Gödel.
In seguito alla dimostrazione di tale teorema era difficile credere che un algoritmo come quello pensato da Hilbert
potesse esistere e Turing cominciò a pensare a come questo potesse essere dimostrato. Cosı̀, iniziò a pensare a come
potesse essere definito, formalmente, un algoritmo, o un passo elementare, ed arrivò alla definizione del linguaggio,
del modello formale di calcolo, che porta il suo nome, la Macchina di Turing.
Turing osservò, poi, che alcune macchine, con certi dati in ingresso si arrestano, mentre altre macchine con altri dati non si arrestano. Come abbiamo già visto dettagliatamente, queste osservazioni unite alla tecnica della
diagonalizzazione di Cantor, portarono Turing a dimostrare l’esistenza di un problema indecidibile.
Prima di procedere, osserviamo che, prima di Turing, Gödel aveva già provato l’esistenza di entità indecidibili. Cerchiamo, allora, di capire cosa aggiunge il lavoro di Turing a quello di Gödel.
Gödel dimostra che esistono proposizioni (vere) di cui non si pu dimostrare la verità; invece, Turing dimostra che non
esiste un algoritmo che verifica se una proposizione è dimostrabile. Proviamo a chiarire questo concetto. “Indecidibile” riferito ad un problema (come quello di Turing) è diverso da “indecidibile” riferito ad un enunciato, come quello
di Gödel. Un problema non è mai una domanda singola, ma un insieme di domande, e la soluzione del problema è un
metodo che si applica uniformemente a tutte le domande che gli appartengono e dà la risposta (appartenenza s` o no)
per ogni caso possibile. Che un enunciato sia indecidibile in una teoria vuol dire soltanto che né lenunciato né la sua
negazione sono dimostrabili nella teoria. Tuttavia esiste un collegamento, che si vede dalla dimostrazione; quando un
problema risulta indecidibile è perché, per ogni metodo risolutivo proposto, esiste un caso particolare in cui il metodo
si blocca e non riesce a dare alcuna risposta, né positiva né negativa; su quel caso particolare, la risposta si comporta
come un enunciato indecidible in una teoria che riguardi le macchine di Turing.
Ciò che ci interessa, in questo paragrafo è comprendere in quale modo la dimostrazione dell’indecidibilità dell’Halting
Problem è in relazione con l’Entscheidungsproblem. A questo scopo, rivediamo in questa ottica i passi principali della
dimostrazione. Ricordiamo che l’idea alla base della dimostrazione era quella di associare un codice numerico (un
numero naturale) ad ogni macchina di Turing e ad ogni input di una macchina di Turing: in tal modo, il codice
numerico associato ad una macchina qualsiasi poteva anche essere dato come input alla stessa macchina. Definiamo,
allora, l’insieme D:
D = { x ∈ N tali che x è il codice di una macchina di Turing e, inoltre, la macchina di Turing che ha
codice x non si ferma con input x }.
La dimostrazione di Turing prova che
Non esiste alcuna macchina di Turing che si ferma su tutti e soli gli input in D.
Definendo l’Entscheidungsproblem, era chiaro ad Hilbert (e, naturalmente non soltanto a lui) che la sua soluzione
avrebbe fornito un algoritmo capace di risolvere ogni problema matematico a patto che esso sia descrivibile nel linguaggio della logica del primo ordine. Quindi, se venisse trovato un problema matematico descrivibile nel linguaggio
della logica del primo ordine per il quale non esiste un algoritmo che lo risolve, questo comporterebbe l’insolubilità
dell’Entscheidungsproblem.
Ora, Turing ha dimostrato che non esiste una macchina di Turing (né, dunque, un algoritmo costitituito da passi elementari ognuno dei quali richiede una memoria di dimensione costante ed il cui esito dipende da un numero costante
di stati) che risolve il problema “n ∈ D?”.
Il problema “n ∈ D?” può essere espresso nella forma di seguito descritta che si avvicina maggiormente al liguaggio
dell’Entscheidungsproblem.
Premessa: [il numero naturale n è il codice di una macchina di Turing] ∧ [il numero n è scritto sul nastro
(per il resto, vuoto) della macchina di Turing che ha codice n]
Conclusione: la computazione della macchina di Turing descritta nella Premessa che ha inizio nello stato
descritto nella Premessa ha termine.
Inoltre, è possibile tradurre entrambe queste proposizioni nel linguaggio della logica del primo ordine. Infine, è
possibile dimostrare che la conclusione può essere derivata dalle premesse utilizzando le regole di tale linguaggio
(ricordiamo, il linguaggio introdotto da Frege) se e soltanto se la computazione in questione termina. Ma questo è
Calcolabilità, 2012/2013
Gli eroi della nostra storia
9
vero se e soltanto se n 6∈ D.
Allora: se esistesse un algoritmo per l’Entscheidungsproblem, potremmo usarlo per decidere l’appartenenza a D.
Ossia, dato un numero naturale n, potremmo usare tale algoritmo per verificare se la Conclusione deriva dalla Premessa: in caso affermativo sapremmo che n 6∈ D, in caso negativo sapremmo che n ∈ D. Dunque, avremmo deciso
l’indecidibile Halting Problem. La conclusione è che l’Entscheidungsproblem è insolubile.
In effetti, ciò che Turing aveva mostrato è che non si può usare una macchina di Turing per risolvere l’Entscheidungsproblem. Per passare da questo risultato alla conclusione che nessun algoritmo può risolvere l’Entscheidungsproblem
aveva utilizzato la sua analisi del processo di calcolo (che lo aveva condotto alla definizione della Macchina di Turing) che lo induceva a ritenere che ogni processo di calcolo poteva essere eseguito da una macchina di Turing. Per
consolidare questa tesi, egli non solo dimostrò che le sue macchine potevano eseguire una moltitudine ci calcoli matematici complessi, ma ebbe l’idea di costruire una macchina di Turing capace di svolgere, da sola, i compiti di tutte le
macchine di Turing: progettò, cosı̀, la Macchina di Turing Universale.
6.7
Autoreferenzialità e paradossi
Il paradosso del mentitore è il seguente:
Io sto mentendo.
Questo è effettivamente un paradosso. Infatti, potete credermi?
Supponiamo che mi crediate: allora starei dicendo la verità, ossia, sarebbe vero che sto mentendo. Ma se stessi mentendo non potrei certo dire la verità.
Allora, meglio non credermi. Cioè, sto affermando il falso. Dunque, non è vero che sto mentendo. Ma se non sto
mentendo, allora sto dicendo la verità, mentre io affermo che sto mentendo . . .
Un filo conduttore collega l’antinomia di Russell, il paradosso del mentitore, la dimostrazione del Teorema di Incompletezza di Gödel e l’Halting problem di Turing, e tale filo è il concetto di autoreferenzialità. Autorefernzialità è una
situazione in cui una entità è chiamata ad operare su sé stessa: il mentitore afferma una verità riferita alla menzogna
contenuta nella sua stessa affermazione, Russell ha individuato un insieme che nulla poteva affermare circa la propria appartenenza a sśtesso, la proposizine U di Gödel afferma la propria indimostrabilità, Turing si interroga circa la
terminazione di una macchina il cui input è sé stessa.
Tuttavia, esiste una profonda asimmetria fra il ruolo giocato dall’autorferenzialità dell’antinomia di Russell e quello
giocato nelle prove di indecidibilità di Turing e di Gödel.
L’autorferenzialità ha, evidentemente, avuto per Russell un ruolo sostanzialmente negativo. Individuando l’antinomia
che porta il suo nome, Russell ha mostrato che il modo in cui stavano cercando di fondare la matematica aveva in sé
qualcosa di intrinsecamente contraddittorio e che, dunque, andava corretto. In altre parole, cercando di convincersi
che la Teoria degli Insiemi di Frege costituiva un sistema di fondamenti per la matematica valido, Russell si è scontrato
(diciamo cosı̀, per caso) con l’antinomia e ha dovuto ricredersi.
Di contro, Gödel e Turing hanno coscientemente cercato una situazione paradossale nel tentativo (riuscito) di dimostrare l’incompletezza dei sistemi sui quali stavano lavorando. Dimostrare l’incompletezza di un sistema, infatti, significa
provare l’esistenza di una entià che in quel sistema può essere descritta ma che in quel sistema non è contenuta. La
tecnica principe in quest’ottica è, naturalmente, la diagonalizzazione di Cantor. Il ricorso all’autoreferenzialità, poi,
ha permesso a Gödel e Turing di costruire le entità “diagonali” cercate.
Con Gödel e Turing, quindi, il ricorso all’autorefernzialità è voluto (anzi, cercato). Ossia, l’autoreferenzialit diventa
uno strumento di lavoro a tutti gli effetti, ed il ricorso al paradosso una nuova tecnica di dimostrazione.
Concludiamo questo (breve) racconto della storia della calcolabilità con una frase che ben riassume lo spirito della
questione:
“Se è vero che un problema non si capisce a fondo finché non lo si deve insegnare a qualcuno altro, a maggior ragione
nulla è compreso in modo pi approfondito di ciò che si deve insegnare ad una macchina, ovvero di ciò che va espresso
tramite un algoritmo.”
Donald Knuth
Calcolabilità, 2012/2013
Gli eroi della nostra storia
10
Appendice. Macchine e Algoritmi
Era dai tempi di Leibniz che si pensava alle macchine calcolatrici, ma prima di Turing si era sempre supposto che
macchina, programma e dati fossero entità completamente distinte. La macchina era un oggetto fisico, quello che oggi
chiameremmo hardware; il programma era la sequenza di istruzioni che la macchina doveva eseguire, e che poteva
essere realizzato mediante una serie di schede perforate; infine, i dati erano l’ingresso numerico.
La Macchina Universale di Turing dimostrava che, da un punto di vista logico, queste distinzioni erano fittizie. Sui
primi due nastri della nostra implementazione della Macchina Universale sono registrati i dati e la sequenza di quintuple della macchina di cui vogliamo simulare la computazione. Questa sequenza, dunque, è vista ed utilizzata dalla
Macchina Universale esattamente allo stesso modo in cui sono visti e trattati i dati; d’altra parte, la sequenza di quintuple si comporta esattamente come un programma che fornisce alla Macchina Universale le istruzioni per una corretta
esecuzione del calcolo sui dati.
Riflettiamo, ora, sul processo di esecuzione di un programma da parte di un moderno calcolatore. Un programma
scritto in un qualsiasi linguaggio di programmazione ad alto livello non è altro che un insieme di dati che vengono
utilizzati dall’interprete o dal compilatore i quali lo elaborano, trasformandolo in modo tale che le sue istruzioni
possano essere eseguite.
A ben guardare, la Macchina di Turing Universale è il primo esempio di programma interprete: passo dopo passo,
essa individua la quintupla che deve eseguiure, la decodifica e la esegue. Ancor più specificatamente, la Macchina di
Turing Universale fornisce un modello di interprete con programma memorizzato (piuttosto che fisicamente realizzato
su qualche supporto esterno alla macchina), in cui le quintuple scritte sul nastro svolgono il ruolo del programma ma
senza che la macchina faccia distinzioni sostanziali fra i dati ed il programma.
In conclusione, l’analisi di Turing offriva una visione nuova e profonda dell’antica arte del calcolo, rivelando che la
nozione di calcolo andava ben oltre i tradizionali calcoli aritmetici e algebrici.
Nota
Molto del materiale di questa dispensa è liberamente tratto da M. Davis :“Il calcolatore universale”, che, nuovamente,
invito tutti a leggere. L’intento divulgativo e la chiarezza espositiva lo rendono una fonte di stimolo intellettuale e un
ottimo strumento di approfondimento.
Calcolabilità, 2012/2013
Gli eroi della nostra storia
11