Studente ........................................................................
Matricola ...........................................
Data ............................................................
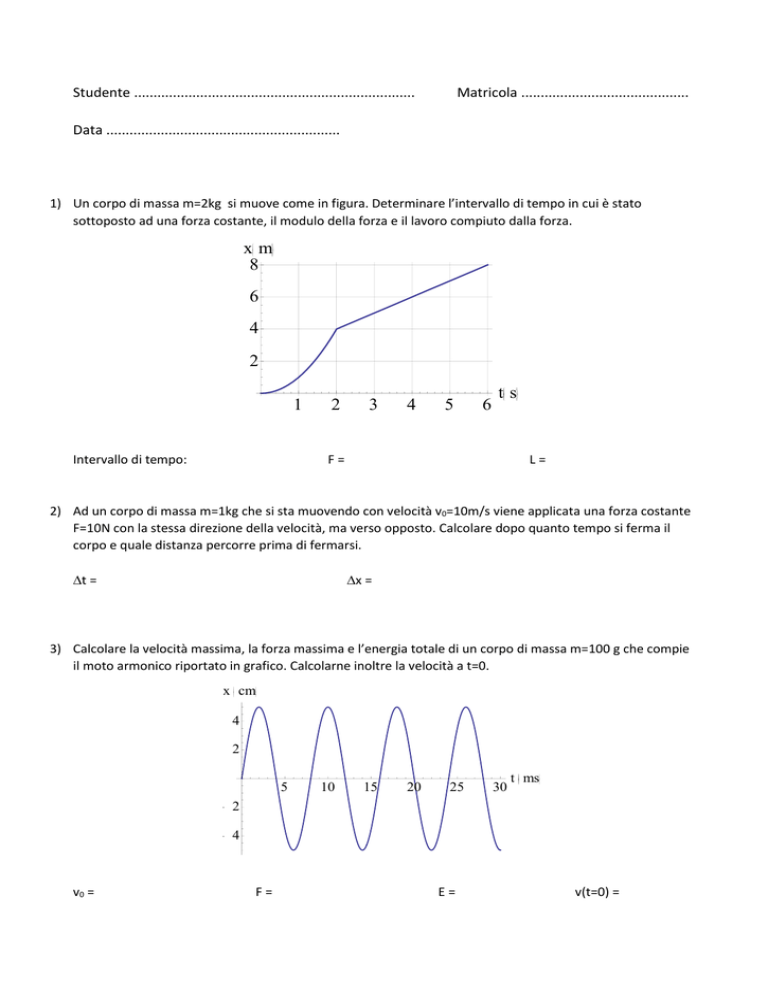
1) Un corpo di massa m=2kg si muove come in figura. Determinare l’intervallo di tempo in cui è stato
sottoposto ad una forza costante, il modulo della forza e il lavoro compiuto dalla forza.
xm
8
6
4
2
1
Intervallo di tempo:
2
3
4
5
6
ts
F=
L=
2) Ad un corpo di massa m=1kg che si sta muovendo con velocità v0=10m/s viene applicata una forza costante
F=10N con la stessa direzione della velocità, ma verso opposto. Calcolare dopo quanto tempo si ferma il
corpo e quale distanza percorre prima di fermarsi.
t =
x =
3) Calcolare la velocità massima, la forza massima e l’energia totale di un corpo di massa m=100 g che compie
il moto armonico riportato in grafico. Calcolarne inoltre la velocità a t=0.
x cm
4
2
5
10
15
20
25
30
t ms
2
4
v0 =
F=
E=
v(t=0) =
4) Un corpo viene lanciato dal suolo verso l’alto con una velocità v0=10 m/s diretta a 30° dall’orizzontale.
Calcolare l’altezza massima h raggiunta, la distanza d percorsa in orizzontale prima di toccare nuovamente il
suolo. Calcolare inoltre modulo e direzione della velocità finale.
h=
d=
vf =
5) Un corpo di massa m=1g cade in aria con una velocità costante v=10m/s. Calcolare il coeffciente di attrito
viscoso.
=
.
6) Un corpo di massa m=0.1 kg compie un moto circolare uniforme attaccato ad una corda di lunghezza l=40
cm, la quale esercita una forza F=20 N. Calcolare il periodo del moto, la velocità e l’energia cinetica.
T=
v=
E=
7) Discutere in modo sintetico la legge di conservazione dell’energia meccanica, portando un esempio di moto
a cui si può applicare.
8) L’asta in figura, considerata senza peso, può ruotare intorno al punto C. Trovare il modulo della forza F2 (in
funzione di F1) per il quale il sistema è in equilibrio.
3L
F2
L
30°
C
F1
9) Se si trascurassero le forze di attrito, un corpo solido immerso in acqua affonderebbe con una
accelerazione a=3 m/s2. Calcolare la densità del corpo. Calcolare la pressione relativa alla profondità
raggiunta da corpo dopo un tempo t=2s.
=
p=
10) Discutere sinteticamente la legge di Bernoulli, mostrandone l’applicazione ad almeno un problema
riguardante un liquido in un tubo.
11) Un manometro a mercurio ha le due superfici sbilanciate di 20cm. Calcolare la differenza di pressione tra le
due aperture.
p =
12) Un’onda sonora di frequenza =5 kHz si sta propagando in aria. Calcolarne la lunghezza d’onda, e stabilire a
quale intervallo spettrale appartiene. Quale è la frequenza 'percepita da un osservatore che si sta
muovendo verso la sorgente con velocità v=200m/s? Spiegare qualitativamente perchè la velocità di
propagazione dell’onda sonora in acqua sarebbe maggiore.
=
intervallo spettrale:
' =
Propagazione in acqua:
13) Definire sinteticamente la temperatura assoluta di un corpo, e discutere un metodo ideale per misurarla.
14) Ad un volume V=50 cm3 di acqua a T=40°C si fornisce una quantità di calore Q=1x104 cal. Calcolare la
temperatura finale dell’acqua. Parte dell’acqua si è trasformata in vapore? Se la risposta è affermativa,
calcolarne la frazione (calore latente di evaporazione: 2250 J/g).
T=
frazione vapore/liquido =
15) Il cilindro in figura, che ha un estremo scorrevole, è riempito di aria a pressione atmosferica, ad una
temperatura T1= 80°K, e con un volume V=1 litro. Il sistema è in equilibrio con la pressione atmosferica
esterna. Se l’aria all’interno viene successivamente scaldata fino ad una temperatura di 400 °C, ed il pistone
scorre per mantenere la pressione in equilibrio, qual è il nuovo volume dell’aria? Quale è la variazione
percentuale della distanza media d tra le molecole di aria?
d/d =
V=
16) Calcolare il campo elettrico e la differenza di potenziale tra due superfici piane poste ad una distanza
d=0.5mm, su cui è distribuita una carica uniforme di segno opposto, con densità Q/A=0.1 nC/cm2. Una
sferetta di massa m=10 mg, con carica elettrica q=0.1C, parte da ferma dalla superficie con carica
negativa. Calcolare la velocità della sferetta quando arriva sull’altra superficie. (nel SI, 0=8.85x10-12)
V =
E=
v=
17) Calcolare la resistività elettrica del materiale che compone un tratto di metallico di sezione A=1mm2,
lunghezza L=100m e resistenza R=4. Calcolare poi la corrente che scorre nel filo quanto ai suoi capi è
applicata una differenza di potenziale V=100V, e la carica totale q che attraverso una sezione del filo in
un intervallo di tempo t=10s. Calcolare inoltre la potenza elettrica dissipata P.
e =
P=
i=
q =
18) Definire sinteticamente il campo elettrico, e descrivere un metodo per creare un campo elettrico costante.












