Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Moto Accelerato
Quando la velocità di un corpo varia nel tempo si dice che esso è
sottoposto ad una accelerazione.
In particolare, nel tempo, il vettore velocità può variare modulo,
direzione o verso. Se uno (o più) di questi tre elementi varia nel tempo
allora il corpo sta subendo una accelerazione.
In un moto unidimensionale la direzione del vettore velocità non
cambia nel tempo, dunque varia solamente il modulo.
v0
vf
x0
xf
t0
tf
1
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
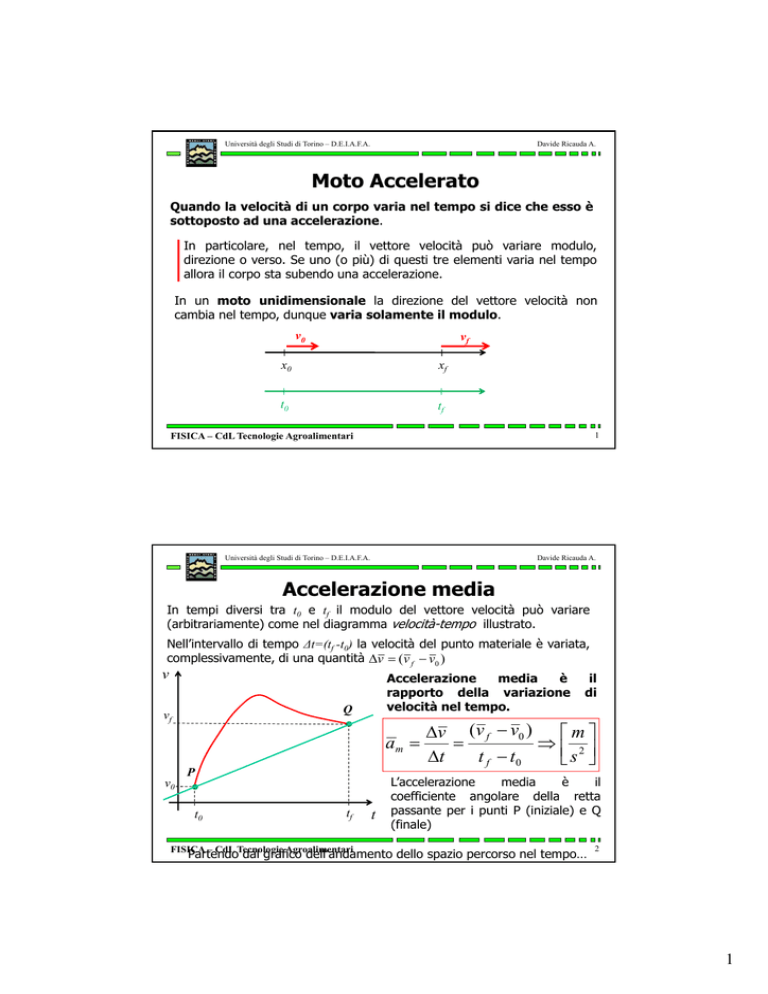
Accelerazione media
In tempi diversi tra t0 e tf il modulo del vettore velocità può variare
(arbitrariamente) come nel diagramma velocità-tempo illustrato.
( f -t0) la velocità del punto materiale è variata,
Nell’intervallo di tempo Δt=(t
complessivamente, di una quantità Δv = (v f − v0 )
v
Accelerazione
media
è
rapporto della variazione
velocità nel tempo.
Q
vf
am =
v0
P
t0
tf
t
il
di
Δv (v f − v0 )
⎡m⎤
⇒⎢ 2⎥
=
Δt
t f − t0
⎣s ⎦
L’accelerazione
media
è
il
coefficiente angolare della retta
passante per i punti P (iniziale) e Q
(finale)
Partendo dal grafico dell’andamento dello spazio percorso nel tempo…
FISICA – CdL Tecnologie Agroalimentari
2
1
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Accelerazione istantanea (1)
Accelerazione del punto in un qualsiasi istante di tempo, ossia in un
qualsiasi punto del grafico velocità-tempo.
DEFINIZIONE:
L’accelerazione istantanea è il limite per Δt Æ 0 dell’accelerazione
media calcolato in un genetico istante di tempo t
v
v
vf
v0
Q
Accelerazione istantanea è la
pendenza della retta tangente al
grafico velocità-tempo nel generico
istante di tempo t.
P
t0
tf
t
t
3
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Accelerazione istantanea (2)
Poiché
a =
dv
dt
, allora l’accelerazione istantanea può essere espressa
come derivata seconda del vettore velocità rispetto al tempo.
tempo
Se il vettore accelerazione ha lo stesso verso del vettore velocità allora la
velocità aumenta (accelerazione).
Se il vettore accelerazione ha lo verso opposto al vettore velocità allora la
velocità
l ità diminuisce
di i i
(
(accelerazione).
l
i
)
FISICA – CdL Tecnologie Agroalimentari
4
2
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Moto uniformemente accelerato (1)
Il vettore accelerazione istantanea è costante in modulo direzione e verso
in qualunque istante t Æ la pendenza della retta tangente alla traiettoria è
sempre costante.
Il modulo della velocità cresce (decresce) linearmente nel tempo.
v
a ≡ am
Q
vf
Δv
a ≡ am = ⇒ Δv = a ⋅ Δt
Δt
Δv
v0
P
Δt
t0
tf
t
5
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Moto uniformemente accelerato (2)
Normalmente l’istante t0=0, per cui, confondendo i vettori con il loro
modulo,
l’equazione
fondamentale
del
moto
rettilineo
p
come:
uniformemente accelerato si esprime
v = v 0 + a ⋅ t ⇒ v = v0 + a ⋅ t
v
La quale, nel caso di velocità
iniziale nulla (v0=0), diventa:
v = v0 + a ⋅ t
v
v = a ⋅t
v = a ⋅t
v0
t
FISICA – CdL Tecnologie Agroalimentari
t
6
3
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Legge oraria (1)
L’equazione fondamentale del moto rettilineo uniformemente
accelerato lega la velocità di un punto materiale al tempo attraverso
l’accelerazione.
Essa, però, non descrive il moto del corpo in quanto non determina la
posizione del punto, lungo la retta in cui avviene il moto, al trascorrere del
tempo t, cioè non è una legge oraria.
C
Come
ricavare
i
lla llegge oraria?
i ?
7
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Legge oraria (2)
IDEA DI PARTENZA:
Si è detto che la velocità istantanea è la derivata dello spazio rispetto al
tempo calcolata in un generico istante di tempo t.
L’integrale della velocità istantanea identifica lo spazio percorso tra
l’istante iniziale t0 e il generico istante t.
v (t ) =
dx ( t )
⇔ x (t ) =
dt
t
∫ v (t )
dt
t0
Lo spazio percorso equivale all’area compresa tra il grafico
velocità-tempo e l’asse t.
FISICA – CdL Tecnologie Agroalimentari
8
4
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Legge oraria (3)
Nel caso di moto rettilineo uniformemente accelerato, la curva nel grafico
velocità-tempo è una retta di equazione v = v 0 + a ⋅ t
Area compresa tra il grafico
velocità-tempo e l’asse t è un
trapezio.
v
v
a ⋅t
A2
v0
v = v0 + a ⋅ t
v0
A1
t
Si può scomporre nella somma
di un rettangolo più un triangolo
t
x ( t ) = A1 + A 2
9
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Legge oraria (4)
Rettangolo:
Triangolo:
base = t
altezza = v0
base = t
altezza = a ⋅ t
v
v
a ⋅t
A2
v0
v = v0 + a ⋅ t
v0
A1
t
x ( t ) = A1 + A 2 = v 0 ⋅ t +
x (t ) = v 0 ⋅ t +
FISICA – CdL Tecnologie Agroalimentari
t
1
t ⋅ (a ⋅ t )
2
1
a ⋅t2
2
10
5
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Equazioni cinematiche del
moto uniformemente accelerato
v = v0 + a t
1
at2
2
+ 2 a (x − x 0
Velocità in funzione del tempo
x − x0 = v0 t +
v 2 = v0
2
Legge oraria (spazio funz. del tempo)
)
Velocità in funzione dello spostamento
ATTENZIONE!!! Se l’accelerazione è opposta al senso del moto,
cioè opposta al vettore velocità, risulta essere negativa.
11
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
ESEMPIO (1)
Un’auto, partendo da ferma impiega 5 s a raggiungere una velocità di
100km/h. Quale distanza viene coperta in tale tempo?
Se subendo la stessa accelerazione la stessa auto avesse una velocità
iniziale di 30 km/h, quale distanza verrebbe coperta nel medesimo tempo?
Quale sarebbe la sua velocità finale?
a
v0=0
vf =100km/h
Caso 1: Auto parte da ferma
x0=0
xf
t0=0
tf
Per determinare lo spazio percorso dall’auto occorre applicare la legge
oraria del moto uniformemente accelerato.
FISICA – CdL Tecnologie Agroalimentari
12
6
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
ESEMPIO (2)
Nell’applicarla occorre tenere conto
come x0.
che la velocità iniziale è nulla così
x − x0 = v0t +
x =
1
a t
2
2
1
at
2
2
Incognita
L’accelerazione a può essere ricavata dalla relazione fondamentale:
v f = v 0 + at = at ⇒ a =
vf
t
ATTENZIONE!!! La velocità è espressa in km/h Æ occorre convertirla in
m/s: 100km/h=100/3.6 m/s=27.78 m/s
13
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
ESEMPIO (3)
Dall’ultima equazione si ricava a=5.56 ms-2 e sostituendo tale valore
nell’equazione
nell
equazione precedente si ottiene xx=69.44
69.44 m.
Caso 2: Auto con velocità iniziale 30km/h=8.33 m/s
a
v0=30km/h
vf =100km/h
x0=0
xf
t0=0
tf
In questo caso la velocità iniziale non è nulla.
FISICA – CdL Tecnologie Agroalimentari
14
7
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
ESEMPIO (4)
x = v0t +
1
at
2
2
= 8 . 33
1
m
m
2
⋅5s +
5 . 56 2 (5 s )
2
s
s
41.65 m
69.44 m
Notare che il contributo dato dal termine di accelerazione è identico a
prima!
L velocità
La
l ità finale
fi l in
i questo
t caso vale:
l
vf
m
= v 0 + at = 8 . 33
+
s
m
s 2 = 36 . 11 m = 130 km
s
h
5s
5 . 56
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
15
Davide Ricauda A.
ESEMPIO (5)
FISICA – CdL Tecnologie Agroalimentari
16
8
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Strategia risolutiva dei problemi
1. Assicurarsi che tutte le unità di misura dei dati del problema siano
espresse secondo il SI.
2. Tracciare uno schizzo che illustri il problema.
3. Scegliere un sistema di riferimento concorde con il senso del moto.
4. Inserire le posizioni ed i vettori velocità ed accelerazione con il verso
appropriato (il verso stabilirà il loro segno).
5 Rifl
5.
Riflettere
tt
su ciò
iò che
h accade
d fisicamente
fi i
t nell problema
bl
d
descritto
itt e
selezionare le equazioni cinematiche sulla base dei dati in possesso e
delle incognite.
6. Ricordarsi che i vettori discordi con il senso del moto determinano un
segno negativo delle corrispondenti grandezze nelle equazioni.
17
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Corpi in caduta libera (1)
Oggetto in caduta libera è un oggetto che si muove liberamente
sotto ll’azione
azione della gravità, INDIPENDENTEMENTE dal suo stato
di moto iniziale.
Quindi sono corpi in caduta libera quelli:
• Lasciati cadere da fermi (Veloc. Iniziale nulla)
• Lanciati verso il basso (Veloc. Iniziale NON nulla verso il basso)
• Lanciati verso ll’alto
alto (Veloc. Iniziale NON nulla verso ll’alto)
alto)
Tutti i corpi in caduta libera sono soggetti ad una stessa
accelerazione costante diretta verso il basso g=9.81 ms-2.
FISICA – CdL Tecnologie Agroalimentari
18
9
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Corpi in caduta libera (2)
Siccome l’accelerazione di gravità (g) è costante in modulo
direzione e verso si tratta di un moto uniformemente accelerato
quindi valgono le stesse equazioni cinematiche in cui al termine
“a” si sostituisce “g”.
• Moto verso il basso Æ Moto uniformemente accelerato
• Moto verso l’alto Æ Moto uniformemente decelerato
NB Nello
NB.
N ll studio
t di dei
d i corpii in
i caduta
d t libera
lib
sii trascura
t
sempre
l’effetto dell’aria (come se avvenissero nel vuoto) quindi,
indipendentemente dalla loro massa (es. piuma e martello), due
oggetti lanciati dalla stessa altezza toccano terra nel medesimo
istante.
FISICA – CdL Tecnologie Agroalimentari
19
10












