2
√3
1
SCALENO
1
√2
6
1
ISOSCELE
4
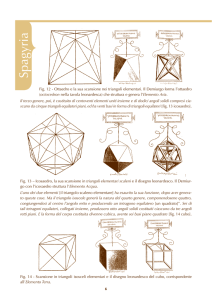
fig. 10
«Dei due triangoli l’isoscele ha avuto una sola natura, lo scaleno infinite. Di queste infinite, dunque, bisogna scegliere la più bella, se vogliamo cominciare in modo conveniente... dunque noi dei molti triangoli
scaleni ne proponiamo uno come il più bello, tralasciando gli altri, ossia quello da cui deriva la costituzione di un terzo, quello equilatero... dunque si scelgono due triangoli, coi quali sono stati prodotti il corpo
del Fuoco e i corpi degli altri Elementi: l’uno sia isoscele, e l’altro che abbia il quadrato del lato maggiore
triplo del quadrato del minore. Ma ciò che in precedenza fu detto in maniera non chiara, ora bisogna
definirlo meglio. Infatti i quattro generi ci sembravano che avessero tutti quanti una reciproca generazione, ma questa non era se non una apparenza non giusta. Infatti nascono, dai triangoli che abbiano scelto,
quattro generi, tre dei quali da quel solo triangolo che ha i lati diseguali [3], mentre il quarto, e questo
solo, è costituito dal triangolo isoscele [2 lati diseguali].Non tutti possono dunque sciogliersi gli uni negli
altri, da molti piccoli diventare pochi grandi e viceversa, ma per i tre primi è possibile. Infatti essendo nati
tutti da un solo triangolo, una volta scioltisi i più grandi, se ne formano da essi molti piccoli, accogliendo
le forme a loro convenienti e quando i molti piccoli a loro volta si dissolvono nei triangoli elementari,
formandosi una unità di una unica massa, se ne forma un altro genere grande».
Con 4 Triangoli equilateri, formati ognuno da 6 triangoli scaleni rettangoli, quindi con 24 triangoli elementari, combinati in modo che ogni gruppo di 3 angoli formi un angolo solido (e pertanto complessivamente 4 angoli solidi), si forma il tetraedro o piramide, che produce, strutturandolo atomisticamente,
il Fuoco (fig. 11).
Fig. 11 – tetraedro, scansione leonardesca2. Elemento Fuoco.
«Ora sarebbe conveniente dire come si sia generato ciascun genere di essi e per il concorso di quali numeri. Si inizierà col primo genere, il più piccolo costituito. Elemento di esso è il triangolo che ha l’ipotenusa doppia del lato minore. Componendosi tali triangoli a due a due per la diagonale, e ripetendosi questo
per tre volte, in modo che i cateti minori convergano in uno stesso punto come in un centro, si genera un
solo triangolo equilatero di sei di numero che erano. Componendosi insieme, poi, quattro triangoli equilateri, ogni gruppo di tre angoli piani costituisce un angolo solido, il quale viene subito dopo il più ottuso
degli angoli piani. E di quattro di tali angoli si costituisce il primo genere di solido [fig. 11 tetraedro], che
ha la proprietà di dividere in parti simili e uguali tutta la superficie delle sfere in cui è iscritto».
Il secondo, poi, è costituito dagli stessi triangoli, ma composti insieme in otto triangoli equilateri, in modo
da fare un angolo solido di quattro angoli piani; ed ottenuti sei di questi, anche il secondo corpo risulta
compiuto [fig. 12 ottaedro].
Questo, come i successivi, è preso dal testo di Luca Pacioli, De Divina Proporzione, 1494.
2
5