Sistema arciere-arco
Consideriamo un ragazzo su uno skateboard mentre cade.
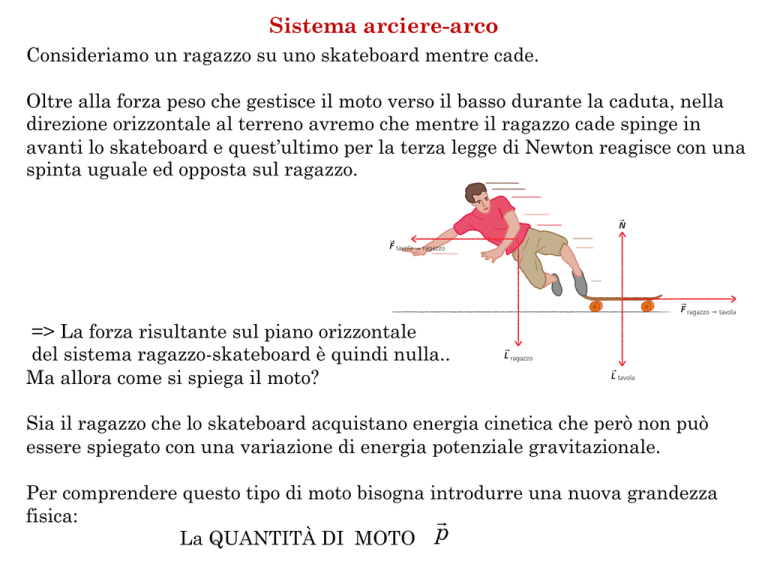
Oltre alla forza peso che gestisce il moto verso il basso durante la caduta, nella
direzione orizzontale al terreno avremo che mentre il ragazzo cade spinge in
avanti lo skateboard e quest’ultimo per la terza legge di Newton reagisce con una
spinta uguale ed opposta sul ragazzo.
N
F tavola
ragazzo
F ragazzo
=> La forza risultante sul piano orizzontale
del sistema ragazzo-skateboard è quindi nulla..
Ma allora come si spiega il moto?
L ragazzo
L tavola
Sia il ragazzo che lo skateboard acquistano energia cinetica che però non può
essere spiegato con una variazione di energia potenziale gravitazionale.
Per comprendere questo tipo di moto bisogna introdurre una nuova grandezza
fisica:
!
La QUANTITÀ DI MOTO p
tavola
Quantità di moto(1)
!
p
Nuova grandezza : la quantità di moto
Ø La quantità di moto di un corpo di massa m è un vettore pari al prodotto
della vettore velocità moltiplicato per la massa del corpo stesso
!
!
p = mv
Ø La quantità di moto ha stessa direzione e verso del vettore velocità
Ø Questa grandezza racchiude in sé sia le proprietà di moto del corpo che di
resistenza alla modifica di tale moto .
Ø La quantità di moto ha un significato più generale della massa o della velocità
prese singolarmente, e distingue tra corpi di masse diverse che si muovono con
stessa velocità.
Ø Le dimensioni della quantità di moto sono [M][L][T]-1 e l’unità di misura è kg·m/s
Ø La quantità di moto di un corpo spesso è chiamata “momento! del corpo”
Ø Se il corpo si muove in una direzione qualsiasi dello spazio, p si può descrivere
mediante le sue tre componenti lungo x,y e z:
!
p = px î + py ĵ + pz k̂
dove:
! p = mv
x
## x
" py = mvy
#
#$ pz = mvz
Quantità di moto(2)
La quantità di moto permette di definire la seconda legge di Newton in una forma
generalizzata.
!
!
F = ma vale infatti solo nel caso in cui m rimanga
La forma che abbiamo visto :
costante.
Riformulando questa legge mediante la quantità di moto, si includono anche i casi
un cui m varia.
Legge di Newton generalizzata:
La variazione della quantità di moto di un corpo nell’unità di tempo (cioè
la derivata temporale della quantità di moto) è proporzionale alla
risultante delle forze che agisce sul corpo ed ha la stessa direzione
∑
! dp!
∑ F = dt
Forma generalizzata
della 2° legge di
Newton
La quantità di moto di una particella varia se su di essa è applicata una
forza risultante non nulla
Se la risultante delle forze agenti su corpo è nulla la quantità di moto del
corpo rimane costante:
!
!
!
dp
Se: ∑ F = 0 ⇒
= 0 ⇒ p = costante
dt
Quantità di moto(3)
Naturalmente se m è costante le due formule coincidono:
!
!
!
! dp! d mv
!
dm !
dv
dv
F
=
=
=
v
+
m
=
m
=
m
a
∑ dt dt
dt
dt
dt
!
( )
0
Ma come si applica il concetto di quantità di moto ad un sistema
costituito da due o più particelle?
Vediamo di descrivere i sistemi di particelle in termini di forze applicate
Sistemi di punti materiali -Forze interne ed esterne
!
F ji
Fij = − F ji
Pi
Pj
!
Fij
Ø Consideriamo un sistema di n punti materiali, interagenti tra loro e con il resto
dell’universo.
Ø In generale sul punto
! I j agiranno forze esercitate dagli altri n-1 punti materiali
dette forze
! E interne F e le forze esercitate da agenti esterni al sistema, dette forze
esterne F .
Ø La forza agente sul singolo punto j e’ data dalla risultante di tutte le forze agenti:
!
!I
!E
Fj = ∑ Fnj + ∑ Fk
n
k
Ø Per le forze
interne vale il principio!di azione e reazione: per ogni forza
!
interna Fij esiste un’altra forza interna F ji tale che Fij =- Fji .
Sistemi di punti materiali -Forze interne ed esterne
!
!
!E
Fj = ∑ Fnj + ∑ Fk
n
k
Ø Consideriamo la risultante di tutte le forze agenti su tutti i punti di un sistema:
!
!
!
! E ⎞ !I !E
⎛
R = ∑ F j = ∑ ⎜ ∑ Fnj + ∑ Fk ⎟ = R + R
j
j ⎝ n
k
⎠
Risultante delle forze
agenti sul j-simo
puntodel sistema
Somma di tutte le
forze INTERNE
agenti sul
j-simo punto del
sistema
Somma di tutte le
forze ESTERNE
agenti sul j-simo
punto del sistema
Ø Le forze interne si annullano a coppie quindi:
Somma di tutte
le forze
INTERNE
agenti sul
sistema
Somma di tutte
le forze
INTERNE
agenti sul
sistema
!I
! ⎞
!
⎛
R = ∑ ⎜ ∑ Fnj ⎟ = ∑ Fnj = 0
j ⎝ n
⎠ jn
Si ha che:
La risultante delle forze agenti su un sistema è pari alla risultante delle
sole forze esterne
! !E
R=R
!E
⎛
⎞
!E⎟
⎜
dove: R = ∑ ⎜⎜∑ Fk ⎟⎟
j
⎝
k
⎠
Un sistema per il quale la risultante
delle forze esterne agenti su di esso è
!E
nulla si dice ISOLATO => R = 0 → Sistema isolato
Un sistema che non scambia massa con l’esterno si dice CHIUSO
Quantità di moto di un sistema isolato
Se consideriamo un sistema! isolato (RE=0) , costituito da due o più particelle
la quantità di moto totale P di tale sistema, dato dalla! somma delle
!
quantità di moto delle particelle che lo compongono ( P = ∑ pi ) , si conserva
i
Per semplicità consideriamo un sistema costituito da due particelle
di massa m1 ed
m2 che interagiscono tra di loro.
L’interazione tra le due palline! per il
! terzo principio della dinamica avviene
mediante una coppia di forze
! F12 !e F21 tali che: !
!
F12 = − F21
F21 + F12 = 0
Per il secondo principio della dinamica questa relazione si può riscrivere:
!
!
m1a1 + m2a2 = 0
m1
!
dv1
dt
+ m2
!
dv2
dt
=0
Se la massa delle due particelle rimane costante nel tempo si può trasformare la
somma di derivate in una derivata della somma:
!
!
!
!
d m1v1 d m2v2
d m1v1 + m2v2
+
=0
=0
dt
dt
dt
!
!
! !
!
!
d
m
v
+
m
v
d
p
+
p
dP
Ma:
1 1
2 2
1
2
P = la quantità di moto totale del
=
=
=0
sistema isolato
dt
dt
dt
Si trova quindi che:
!
in un sistema isolato la variazione
dP
della quantità di! moto totale del
=0
dt
sistema è nulla e P rimane costante
(
(
) (
)
(
)
(
)
!
P = costante
)
Esempio dell’arciere
Un arciere di massa mA= 60kg è fermo su un blocco di ghiaccio ( assenza di attrito)
e tira una freccia di massa mF= 0.50 kg orizzontalmente a 50m/s.
L’arciere comincerà a muoversi immediatamente dopo il lancio?
Se sì, con quale velocità ?
Questo esercizio può essere svolto solo utilizzando la conservazione
della quantità di moto del sistema ARCIERE-FRECCIA
Il sistema in realtà non è isolato in quanto sia sulla freccia che sull’arciere agisce
la forza gravitazionale e la normale . Queste forze però sono perpendicolari al moto
del sistema. Non esistono quindi forze esterne che agiscono lungo l’asse orizzontale
e possiamo considerare il sistema isolato lungo tale direzione.
La quantità di moto totale del sistema lungo la direzione orizzontale si deve
conservare:
mAvA + mF vFx = mAvAi + mF vFi = mAvAf + mF vFf = costante
x
Poiché prima del lancio la quantità di moto del sistema era nulla anche dopo il
lancio essa dovrà risultare nulla, quindi poiché la freccia si muove anche l’arciere si
dovrà muovere in modo da compensare con la sua quantità di moto la quantità di
moto della freccia:
m
mAvAi + mF vFi = 0
mAvAf + mF vFf = 0
vAf = −
F
mA
vFf = −0.42m s
Impulso e quantità di moto
Abbiamo visto che la !quantità! di moto di una particella varia se su di essa agisce
!
una forza risultante Ftot = ∑ F non nulla:
!
Ftot =
dp
dt
Riscriviamo questa relazione esplicitando dp e quindi integriamo per ottenere la
variazione della quantità di moto nell’intervallo di tempo Δt=tf -ti:
! !
dp = Ftotdt
Integrando
entrambi i
membri
f
! !
!
!
∫ dp = pf − pi = Δp =
i
tf
∫
!
Ftot dt
ti
Questo integrale della forza rispetto al tempo è definito IMPULSO DELLA FORZA
!
I=
tf
∫
!
I
!
!
Ftot dt = Δp
ti
L’impulso è un vettore che ha stessa direzione della variazione della
quantità di moto e le dimensioni della quantità di moto
Quando la forza applicata è costante (nel tempo) l’impulso è dato semplicemente dal
prodotto della forza per l’intervallo di tempo in cui essa è applicata
!
! !
!
Se Ftot =costante ⇒ I = Ftot Δt = Δp
Sistema di corpi NON isolato - IMPULSO
Nel caso di un sistema di particelle sul quale agisce una forza risultante esterna non
nulla e di conseguenza si produce una variazione della quantità di moto totale del
sistema, si ha:
!
!
! tf !
!
dove
R= F
I = R dt = ΔP
∑
∫
ti
est
L’impulso passato ad un sistema è pari alla variazione della quantità di
moto totale del sistema nell’intervallo di tempo Δt
Quindi, quando viene dato ad un sistema un impulso, significa che una certa
quantità di moto viene fornita al sistema dall’esterno.
R
NB: per come è definito l’impulso, graficamente esso è
uguale all’area sottesa alla curva R in funzione di t,
nell’intervallo di tempo compreso tra ti e tf .
R(t)
!
I=
tf
!
∫ ∑ Rdt
ti
Introducendo il concetto media temporale della forza
risultante media
!
1 !
R =
Rdt
∫
Δt
!
R = Fmedia
risultante
media
ti
si può esprimere il teorema dell’impulso
tramite la relazione equivalente:
!
!
!
I = ΔP = R Δt
Nel caso particolare che la forza risultante sia costante !
nel tempo l’impulso può essere riscritto nella forma: I
! !
= ΔP = RΔt
!
se R = costante
Forze impulsive ed urti
Approssimazione dell’Impulso:
Ø In molte situazioni si può assumere che una delle forze agenti su una particella
agisca per un breve intervallo di tempo, ma che in tale intervallo sia molto più
intensa delle altre.
Ø In questa approssimazione si può trascurare il contributo all’impulso da parte
delle altre forze agenti e la variazione di quantità di moto della particella sarà
determinata dall’impulso della sola forza dominante.
Ø Negli urti tra particelle si assume che la mutua interazione tra le particelle
nell’urto sia molto più intensa di tutte le forze esterne.
Ø L’urto può essere dovuto ad un contatto fisico tra due corpi (valido solo a livello
macroscopico) o ad un’interazione molto intensa che non prevede il “contatto
fisico” ( urto a livello microscopico)
Ø Quando due particelle di massa m1 ed m2 si urtano e consideriamo queste due
particelle
!
!come un sistema isolato, la loro quantità di moto totale si conserva infatti
se Δp1 e Δp2 sono le variazioni dell’impulso delle due particelle durante l’urto:
!
Δp1 =
f
∫
!
F21 dt
!
Δp2 =
i
!
!
Δp1 + Δp2 = 0
f
∫
!
F12 dt
!
!
dove F12 = − F21
!
!
Δp1 = −Δp2
i
!
!
!
!
p1 − p1 + p2 − p2 = 0
f
i
f
i
! !
Pi = Pf = cost
%
%
%
%
p1i + p2i = p1 f + p2 f
!
"
$
!#
!
" $!#
%
%
Pi
Pf
Urti
Abbiamo appena visto che negli urti si conserva la quantità di moto del
sistema, in generale però NON si conserva l’energia cinetica.
Proprio in funzione del comportamento dell’energia cinetica gli urti vengono
differenziati in tre categorie:
Ø Urti elastici nei quali si conserva anche l’energia cinetica del sistema ΔT=0
Ø Urti anelastici nei quali NON si conserva l’energia cinetica del sistema ΔT≠0
Ø Urti perfettamente anelastici nei quali NON si conserva l’energia cinetica del
sistema (ΔT≠0) ed i corpi dopo l’urto risultano uniti l’uno all’altro e si comportano
come un singolo corpo di massa m1+m2
Mentre la quantità di moto si conserva in tutti i tipi di urti, l’energia
cinetica si conserva solo negli urti elastici










