ALCUNI TEOREMI DI RETROSPETTIVA DI GEOMETRIA EUCLIDEA PIANA
Disegnetti da Fortini-Cateni
Definizione di bisettrice di un angolo: la bisettrice è la semiretta che divide l'angolo al vertice in
due angoli uguali
Si dimostra che, per qualsiasi angolo (convesso, concavo, piatto), la bisettrice esiste ed è una sola.
Accenniamo al caso dell'angolo convesso. Sui lati prendiamo dal vertice A due segmenti uguali
(AD=AE) e congiungiamoli. Prendiamo un punto F all'interno dell'angolo e congiungiamolo a D e a
E. Se l'angolo FDE è diverso da FED, per es., minore, da E tracciamo la semiretta EH che forma un
angolo DEH=EDF e incontra DF nel punto G (postulato). Il triangolo il triangolo DEG è isoscele.
Si considerino i due triangoli ADG e AEG che sono uguali per il III° criterio di uguaglianza dei
triangoli. Ne deriva che la retta AG è la bisettrice. Essa è unica perché ogni altra divide l'angolo al
vertice in pari disuguali.
Consideriamo ora la bisettrice dall'angolo piatto. si prenda un punto D all'interno dell'angolo e lo si
unisca con A; se l'angolo BAD e CAD risultano uguali, la semiretta AD è la richiesta; se invece
sono disuguali, sulla maggiore costruiamo la semiretta AE in modo che l'angolo BAE sia uguale
all'angolo CAD; otteniamo un angolo EAD che è convesso; cioè esiste una semiretta AF che lo
divide in parti uguali.
Semiretta che biseca un convesso
un angolo piatto
un angolo concavo
Unicità della bisettrice nel caso dell'angolo convesso BAC. Ogni altra semiretta AH diversa da AG, lo divide in parti
disuguali. Infatti dalla figura abbiamo BAH>BAG=GAC>HAC a maggior ragione BAH>HAC. IL ragionamento è analogo
per gli altri due angoli c.v.d.
Se l'angolo BAC è concavo, sia AE la semiretta che dimezza l'angolo convesso che ha gli stessi lati. Si tracci la semiretta
AF opposta ad AE che divide l'angolo concavo BAC in due parti uguali. Infatti gli angoli FAB E FAC risultano uguali
perché supplementari (la loro somma è un angolo piatto) dei due angoli uguali BAE e CAE.
_________________________________________
Definizione di perpendicolare: la perpendicolare da un punto esterno P ad una retta è la
semiretta da P che fa due angoli uguali sulla retta, cioè due retti; la perpendicolare tracciata
da un punto O qualsiasi della retta, è la semiretta che parte da O e costruisce due angoli retti
sulla retta.
Come conseguenza, nel caso di una perpendicolare da un punto C (vedere sotto) fuori di una
retta condotto alla retta è esistente ed unica. Facendo ruotare il semipiano di C intorno alla
retta e tornando indietro, ottengo l'immagine del punto C, cioè D nell'altro semipiano. Si
colleghi C e D ottenendo il punto di intersezione sulla retta, O. Vogliamo dimostrare che la
retta CD forma con la retta AB angoli uguali. Ripetendo la rotazione la semiretta OC si
sovrappone alla OD e l'angolo BOC si sovrappone all'angolo BOD e quindi sono uguali e la
retta CD e perpendicolare a AB.
La perpendicolare è unica perché, tracciando CF, si forma il triangolo COE di cui l'angolo CEB è
esterno maggiore di ogni angolo interno non adiacente (anche del retto).
Dimostriamo ora l'esistenza e l'unicità del punto medio di un segmento.
Dalle due figure sopra, dimostrato dalla prima che in un triangolo isoscele la bisettrice
dell'angolo al vertice è perpendicolare alla base e la divide per metà, consideriamo nella
seconda il segmento AB e un punto C, e colleghiamolo con A e B. Se l'angolo CAB è
diverso dall'angolo ABC per es., minore, sul maggiore tracciamo una semiretta BD che
faccia un angolo uguale a CAB e incontri AC nel punto E. Colleghiamo E con F. All'interno
di un angolo, qualsiasi retta dal vertice attraversa sempre i segmenti che collegano qualsiasi
coppia di punti presa sui lati (postulato). Si ha così un triangolo isoscele con gli angoli alla
base uguali (lati obliqui uguali). Tracciamo la bisettrice dell'angolo al vertice AEB che per il
teorema precedente è anche altezza e divide la base in due segmenti uguali. Il punto F è il
punto medio del segmento AB. Esso è unico perché per un qualsiasi altro punto G,
AG>AF=FB>FG, a maggior ragione
AG>GB
_________________________________________________
•I disegnetti successivi sono ripresi da M. Galli
Definizione di rette parallele: due rette sono parallele se, comunque prolungate non si
incontrano mai.
Usando il teorema precedente (esistenza ed unicità della perpendicolare) si dimostra il
teorema che da un punto esterno ad una retta è tracciabile sempre una parallela alla retta
data.
I teoremi descritti fino qui non utilizzavano il V° postulato, come anche i criteri di
uguaglianza dei triangoli e l'esistenza ed unicità del punto medio di un segmento ed altri
L'unicità della parallela per il punto esterno, invece, fa parte del V° postulato così
enunciabile: data una retta e dato un punto P fuori di essa, per il punto P passa una parallela
(teorema) ed una sola (cuore del postulato).
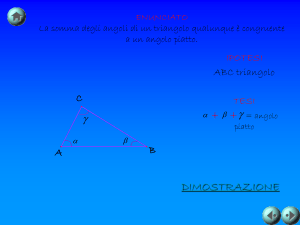
Con il V° postulato si può dimostrare il famoso teorema della somma degli angoli di un
qualsiasi triangolo che afferma che tale somma è pari a 180° (un piatto o due retti). Ciò
significa che il teorema della somma degli angoli interni di un triangolo 'contiene' il V°
postulato, nel senso che presuppone la validità dell'unica parallela.
Senza il V° postulato possiamo dimostrare solo che la somma di due angoli qualsiasi di un
triangolo e minore di due retti, cioè di un piatto o 108°e, nel contesto di questo teorema, si
dimostra anche che ogni angolo esterno di un triangolo è maggiore di ciascuno degli angoli
interni non adiacenti o uguale alla somma dei due angoli interni non adiacenti. Vedere dopo
anche la dimostrazione più articolata di Legendre.
Teoremi dell'angolo esterno di un triangolo
Dato il triangolo ABC si prolunghi il segmento AB e tracciamo una semiretta da A passante
per il punto medio M, che è esistente ed unico (vedere il teorema già dimostrto), del
segmento BC. La semiretta da A a D, interna all'angolo CAB incontrerà certamente
(postulato) il segmento CD che collega una coppia di punti sui due rami dell'angolo. Su tale
semiretta prendiamo un punto D tale che AM=MD. I due triangoli AMC e BMD sono uguali
per il primo criterio di uguaglianza dei triangoli perché hanno uguali gli angoli AMC e BMD
perché opposti al vertice e il lati CM e AM del primo triangolo sono uguali rispettivamente a
a MB e MD del secondo per costruzione. Ma in triangoli uguali a lati uguali si oppongono
angoli uguali, per cui sono uguali gli angoli ACM E MBD (gamma). D'altra parte la somma
degli angoli beta (β) e gamma (γ) sono minori di due retti, in quanto γ è interno all'angolo
esterno, c.v.d.; d'altra parte dalla figura l'angolo esterno (di lati BC e prolungamento di AB)
è maggiore di γ che ne è una parte, per cui è maggiore dell'angolo interno non adiacente,
c.v.d. La dimostrazione può essere ripetuta su ogni lato. Manca la relazione fra l'angolo
esterno e la somma degli interni non adiacenti.
Con il teorema appena dimostrato che la somma di due angoli interni di un triangolo è
minore di due retti, dimostriamo la prima parte del postulato V°, cioè l'esistenza di una
parallela alla retta data per un suo punto esterno.
TEOREMI SULLA PARALLELA
Da P conduciamo la perpendicolare alla retta r; sia questa PQ. Conduciamo per P la retta s
perpendicolare a PQ. Ne consegue che gli angoli alfa (α) e beta (β) sono uguali e retti. Se la retta r
incontrasse la retta s, le due rette con PQ formerebbero un triangolo con la somma degli angoli
superiore a 2 retti. Questo è assurdo per il teorema precedente. Si conclude che le due rette sono
parallele, per cui esiste una retta parallela (la s) alla retta r passante per P.
Ma questa parallela è unica? Ora se consideriamo un'altra retta k passante per P e distinta da r,
siamo sicuri che questa incontri ad un certo punto r? Euclide ipotizza che si incontrino dalla parte
del piano dove la somma degli angoli corrispondenti è minore di 2 retti. Questo è il cuore del quinto
postulato intuitivo, ma forse più complesso degli altri. Il fatto che due rette prolungate non si
incontrano mai (rette parallele), significa che sono anche equidistanti? Nel tempo fu proposto di
definire una parallela ad un'altra come la retta da essa equidistante. La proposizione 'il luogo dei
punti equidistanti da una retta data appartengono ad un'altra retta parallela alla prima', è sostenuto
dalla nostra intuizione, ma non è derivabile dagli altri postulati, come l'unicità della retta parallela
per un punto esterno; in questa proposizione è contenuto già il V° postulato. Quindi si tratta di un
postulato analogo al V°. Se sostituissimo al quinto la detta definizione potremmo dimostrare con
altri postulati e teoremi che la retta passante per P e non intersecante l'altra, è unica, cioè il quinto
postulato!
Gli antichi matematici, come già accennato, tentarono di dimostrare questo strano postulato (croce e
scandalo della geometria elementare, come ebbe a dire D'Alambert), ma i loro tentativi non
sortirono altro effetto che quello di sostituire al postulato di Euclide altri postulati del tutto
equivalenti. Le affermazioni di partenza di questi matematici nascondevano un postulato analogo a
quella da dimostrare!
Così, volendo eliminare il V° postulato, iniziando l'argomentazione con il teorema degli angoli
interni del triangolo dimostrato anche con il V° di Euclide, potremmo raggiungere deduttivamente
anche l'unicità della retta parallela. Dovremmo però sostituire tale teorema come postulato del
sistema al posto del V°. L'obbiettivo di dimostrare il V° eliminandolo falliva, anche perché il nuovo
postulato era meno intuibile del vecchio. Si potrebbe a questo punto continuare a tentare di
dimostrare il teorema degli angoli interni di un triangolo escludendo il V°, indirettamente
trasformando il V° in teorema, ma tutti i tentativi fallirono.
PREMESSA L'EQUIDISTANZA DI DUE RETTE, L' UNICITA' DELLA PARALLELA
SEGUE LOGICAMENTE
Il postulato dell'unicità della retta per il quale non è possibile proporre una logica spiegazione, in
effetti contiene le seguenti proposizione
1 – L'intuizione suggerisce che posano esistere due rette equidistanti, cioè che il luogo dei punti
equidistanti da una retta debba essere un'altra retta.
2 – Se due rette si incontrano in un punto O, è intuibile che presi due punti equidistanti da O,
OP = OQ, se la distanza OP cresce oltre ogni limite anche il segmento PQ cresce oltre ogni limite.
Ammesso questo come postulato dell'equidistanza, è possibile dimostrare che una retta non
equidistante debba incontrare l'altra, cioè l'unicità della retta che diventa un teorema!
Si dimostra col V° postulato che OP e PQ sono direttamente proporzionali. Senza il V°, Euclide
dimostrò che se OP supera ogni limite lo fa anche PQ e dimostrò che una spezzata condotta fra due
punti è più lunga del segmento di retta che li unisce eche in un triangolo rettangolo l'ipotenusa è più
lunga di ogni cateto. Cos in un triangolo rettangolo 'coperto' da una successione di angoli come
quello sopra, di ha: OA < n*AB e AB > OA/n se il segmento OA tende all'infinito lo fa anche AB.
Dalla figura, tenendo conto delle argomentazioni precedenti risulta che spostando M oltre ogni
limite anche il segmento MK fa altrettanto; infatti raddoppiando la figura coll'angolo OKN,
spostando M verso l'infinito, analogamente si comporta il segmento MN come già dimostrato; per
cui anche il segmento MK, cioè la distanza dalla retta OB, la metà di MN, fa altrettanto.
Ne consegue il seguente teorema conclusivo:
Siano r ed s due rette equidistanti (fig. sopra) e sia delta la loro distanza. Si consideri un'altra retta k
che formi con r un angolo alfa piccolo a piacere. Procedendo lungo questa retta la distanza PM
deve crescere oltre ogni limite, uscendo uscendo ad un certo punto dalla striscia compresa fra le due
rette, incontrando la retta s, di qui l'unicità della parallela.
PREMESSA LA SOMMA DEGLI ANGOLI DI UN TRIANGOLO UGUALE A DUE RETTI,
SI PUO' DIMOSTRARE L'UNICITA' DELLA PARALLELA
Si abbia una retta orizzontale v che passa per i punti A e B; da essi tracciamo verso l'alto due rette r
ed r' perpendicolari a v. Si deve dimostrare che r ed r' siano equidistanti (AB=PQ), in quanto
abbiamo dimostrato prima, che equidistanza implica unicità.
I due triangoli APQ e ABQ sono uguali perché hanno due lati uguali e l'angolo compreso
(alfa=alfa1), per il primo criterio di uguaglianza. Alfa è uguale da alfa1 in quanto alfa1+beta1 =90°
e anche alfa+beta1=90° per cui alfa ed alfa1 sono complementari dello stesso angolo beta1.
Alfa1+beta1 sono un retto perché k1= un retto e la somma di alfa1+beta1+k1 (somma angoli di un
triangolo, ipotesi iniziale) = 2 retti. Ne deriva l'uguaglianza di AB=PQ e, poiché la coppia PQ è
arbitraria, le due rette r e r1 sono equidistanti e per il teorema già dimostrato ne consegue l'unicità
della parallela. c.v.d.
Possiamo ottenere lo stesso risultato in un modo diverso. E' necessario introdurre prima un lemma.
Definizione di Lemma: proposizione importante per la dimostrazione di un teorema successivo.
Ammesso come postulato il teorema della somma degli angoli interni di un triangolo, è possibile
come primo passo costruire un triangolo rettangolo con uno degli angoli acuti minore di una
quantità piccola piacere (lemma)
Dalla figura sotto siamo partiti da costruire un triangolo retto e isoscele BAC, sia omega uno degli
angoli acuti uguali. Prolunghiamo AC e sulla prolunga segnamo un punto C1 tale CC1 sia uguale a
BC. Si ha il triangolo isoscele in cui CC1B=CBC1 . I due angoli sono gli interni non adiacenti
dell'angolo esterno ACB. Sapendo che l'angolo esterno di un triangolo è uguale alla somma dei due
interni non adiacenti si ha che l'angolo esterno al triangolo BCC1 è uguale alla somma degli angoli
CC1B+CBC1; se chiamiamo il valore comune dei due angoli non adiacenti ω1, ω=2*ω1 e ω1=ω/2.
Possiamo continuare la costruzione prendendo sul prolungamento di AC il punto c2 tale
C1C2=BC1; ne risulta un nuovo triangolo isoscele BC1C2 con angolo esterno ω/2 e angoli interni
non adiacenti ω/4 e cosi via. Se facciamo n costruzioni come le precedenti si giunge ad un triangolo
rettangolo dove l'angolo sul prolungamento sarà ω/2^n. Se n diventa sempre più grande avremo un
triangolo rettangolo con uno degli angoli acuti piccolo a piacere. c.v.d.
Con il risultato del teorema precedente sarà facile dimostrare l'unicità della parallela.
Dimostriamo il teorema che, se la somma degli angoli interni di un triangolo è due retti (postulato di
partenza), allora è 'vera' l'unicità della parallela, che cessa di essere a sua volta un postulato.
Consideriamo un punto P fuori della retta r. tracciamo da P la perpendicolare ad r incontrata in Q;
conduciamo poi per P la retta s perpendicolare a PQ. Ipotizziamo che la retta s non possa incontrare
la retta r. Conduciamo ora attraverso P un'altra retta non coincidente con s ed ammettiamo che formi
con PQ un angolo inferiore ad un retto, il cui complementare (che è l'angolo che sommato al
precedente dà un retto) lo chiameremo lambda (λ). Costruiamo il triangolo QMP di cateti PQ e QM.
Come abbiamo visto nel precedente lemma, QM potrebbe essere così lungo che l'angolo QMP possa
divenire più piccolo di una quantità qualsiasi assegnata, anche minore di λ. Ammesso che la somma
degli angoli di un triangolo sia due retti, l'angolo che la retta PM forma con s deve divenire minore
di λ. Allora la retta K, interna all'angolo QPM, incontrando PM la r, a maggior ragione incontrerà
anch'essa r. Così ammettendo come postulato il teorema della somma degli angoli di un triangolo,
ammettiamo anche il postulato di Euclide (V°) con tutte le conseguenze. Così la geometria
elementare, anche quella studiata nella scuola media, rimarrebbe immutata nella sostanza. Ma il
teorema degli angoli del triangolo è certamente meno intuitivo del V° postulato, anche se forse più
controllabile con con un esperimento, considerando l'affermazione come un goal regolativo;
difficile sarebbe invece controllare sperimentalmente cosa fa una 'parallela' molto lontano!) DA
CONTROLLARE....
PROPRIETA' RELATIVE ALLA SOMMA DEGLI ANGOLI DI UN TRIANGOLO;
USANDO I POSTULATI EUCLIDEI SENZA IL V°
La dimostrazione è dovuta a Legendre, riportata da Galli, che "In nessun triangolo la somma dei
suoi angoli interni non può mai superare due retti". Come conseguenza si apriranno così le due
possibilità che ; 1) sia uguale a due retti; 2) sia minore di due retti.
Consideriamo la figura sotto analoga a quella precedente per dimostrare i teoremi dell'angolo
esterno di un triangolo. Sia ABC il triangolo primitivo; si prolunghi il lato BC in CD; sia M il punto
medio del segmento BC (che esiste ed è uno solo); si unisca A con M e sul suo prolungamento si
prenda il segmento MC'=AM; si tracci la semiretta di origine B e passante per C';essa cade
necessariamente all'interno dell'angolo CBD dove BD è il prolungamento di AB. Confrontando il
triangolo primitivo ABC con ABC', tenendo conto che gamma=gamma', che epsilon =epsilon', si
vede chiaramente che la somma degli angoli del triangolo ABC è data da epsilon + lambda + beta +
gamma; la somma nel triangolo ABC' è: beta + gamma' + epsilon' + lambda; ne deriva che le due
somme sono rigorosamente uguali.
Inoltre il triangolo ABC' ha un angolo che è minore od uguale alla metà di uno degli angoli del
triangolo di partenza ABC. Infatti la retta AC' divide l'angolo alfa del triangolo ABC in due parti
epsilon e lambda in generale diverse; una cioè lambda, è comune ai due triangoli e l'altra, epsilon è
uguale ad un angolo, epsilon' del nuovo triangolo ABC'. Nel nuovo triangolo allora ci sono due
angoli, epsilon' e lambda che sommati danno alfa, angolo del triangolo primitivo. Se sono uguali,
caso poco frequente, si può affermare che il nuovo triangolo ABC' possiede un angolo che è la
metà di alfa e, se sono diversi, caso più frequente, il nuovo triangolo possiede un angolo minore
della metà di alfa. Concludendo, vedere lo scritto 'arruffato' sulla figura
"qualunque cosa accada, potremo concludere
che il nuovo triangolo possiede un angolo che è minore o al più uguale alla metà di alfa" M. Galli
opera citata.
Ma la costruzione fatta su ABC possiamo ripeterla su ABC' ottenendo un terzo triangolo su cui
applicare lo stesso ragionamento e così via. Supponendo di fare n costruzioni analoghe potremmo
ottenere alla fine un triangolo che ha la stessa somma degli angoli come l'originale ABC e un
angolo molto piccolo, minore od uguale a alfa/2^n, dove alfa è l'angolo del triangolo ABC di
partenza.
CONCLUSIONI DEL TEOREMA DI ADRIEN LEGENDRE (1752-1833) CHE DEFINISCE
GLI INCASTRI POTENZIALMENTE NECESSARI ALLA NASCITA DELLE
GEOMETRIE NON EUCLIDEE, SITUATI SULLA 'SUPERFICIE' DEL TERZO MONDO
DELLE 'IDEE' DI POPPER
Tenendo conto del teorema precedente, ammettiamo, per assurdo, che la somma degli angoli del
triangolo ABC sia maggiore di due retti anche di una quantità molto piccola delta.
SOMMA ANGOLI DI ABC = 2 retti + delta
Nella costruzione precedente a triangoli successivi la somma dei loro angoli non può cambiare per
postulato iniziale e così anche il valore della somma nel triangolo finale, di cui un angolo diventerà
così piccolo da non superare alfa/2^n e gli altri due angoli insieme saranno minori di due retti, come
dimostrato precedentemente, senza usare il V° postulato. Se n è così grande da rendere alfa/2^n
minore di delta avremo che :
SOMMA ANGOLI DI ABC < 2 retti + alfa/2
asserzione che contraddice la formula precedente. Ne consegue che la somma degli angoli di un
triangolo non può mai superare 2 retti! Si apre ora così la possibilità per le due affermazioni
accennate all'inizio.
1 – La somma degli angoli di un triangolo è uguale a due retti.
2 – La somma degli angoli di un triangolo è minore di due retti.
Ma nascosto nelle pieghe del nostro teorema esiste un postulato euclideo fin'ora taciuto! Il
susseguirsi delle nostre costruzioni sarebbe stato impedito dalla lunghezza della retta, in quanto se
AM, che aumenta con n, non potesse essere raddoppiato sul suo prolungamento il processo si
interromperebbe. Il postulato euclideo da focalizzare afferma che la retta è infinita! Una 'retta'
disegnata su una sfera invece ha lunghezza finita, anche se illimitata, aprendo la possibilità per i
triangoli sferici di avere la somma degli angoli interni maggiore di 2 retti.
Siamo giunti nella zona storica di transizione alle Geometrie non euclidee di A. Bolyai (1802-1860),
Nicolai Ivanovic Lobacevsky (1793-1856), geometria iperbolica e per la geometria sferica B.
Riemann (1826-1866) e con questo terminiamo e per entrare nel vivo di questo nuovo ambiente
culturale vedere anche il post riportato in questo blog dal titolo 'Geometria e Natura', a più voci.
GEOMETRIA E SCIENZA FISICA
Dal punto di vista della scienza fisica, l'interesse non va alla geometria non-euclidea come tale ma
al notevole effetto che ebbe sul concetto di spazio nella fisica moderna. Non solo essa condusse ad
una migliore comprensione della natura ipotetica della geometria assiomatica pura, ma alla
chiarificazione del concetto di spazio fisico rispetto allo spazio matematico. Con la scoperta della
geometria non euclidea fu chiaro che non esistevano mezzi a priori, cioè dal punto di vista logico
matematico, quale tipo di geometria avrebbe descritto le relazioni spaziali fra i corpi fisici. Era
naturale quindi interpellare l'esperimento per stabilire se il problema della vera geometria poteva
essere deciso a posteriori. Per la misura degli angoli bisognava rivolgersi ai movimenti astronomici
per ovviare ad errori di misura. Riemann parlò di spazio generalizzato di cui la geometria euclidea,
quella ellittica di Lobacevsky e Bolyai e la sua sferica erano casi particolari, dando impulso allo
sviluppo della moderna analisi tensoriale, che confinata fino ad allora ai problemi di elasticità,
divenne un mezzo essenziale sia per la matematica superiore sia per la fisica teorica.
_____________________________________
Siamo giunti così nella zona storica di transizione alle Geometrie non euclidee, l'iperbolica di A.
Bolyai (1802-1860), Nicolai Ivanovic Lobacevsky (1793-1856), e la geometria sferica di B.
Riemann (1826-1866) e con questo terminiamo, e per entrare nel vivo di questo nuovo ambiente
culturale vedere anche il post riportato in questo blog dal titolo 'Geometria e Natura', a più voci.
Dott. Piero Pistoia