Una nuova quantità: Attrito

Una nuova quantità: Attrito
Cosa fa?
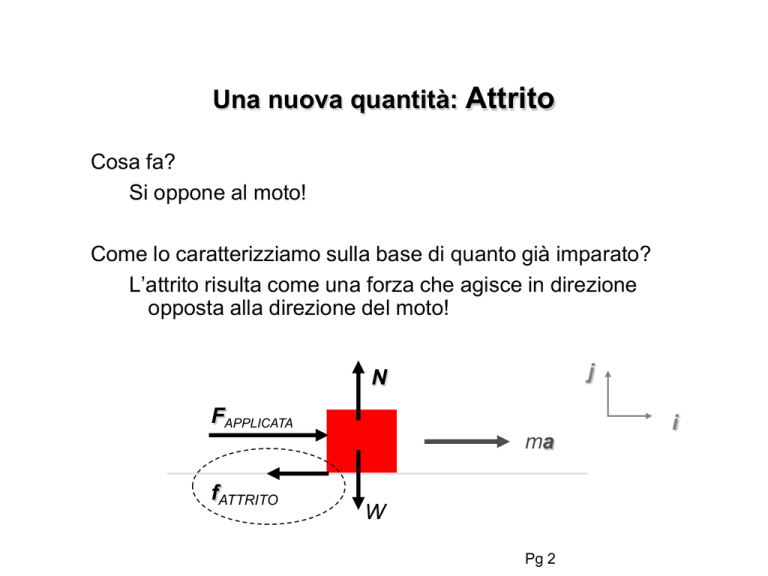
Si oppone al moto!
Come lo caratterizziamo sulla base di quanto già imparato?
L’attrito risulta come una forza che agisce in direzione
opposta alla direzione del moto!
j
N
FAPPLICATA
ma
fATTRITO
W
Pg 2
i
Attrito...
L’attrito è causato dall’interazione “microscopica” fra due
superfici :
Pg 3
Attrito...
La forza di attrito agisce in opposizione al moto :
Parallelamente alla superficie.
Perpendicolare alla forza Normale.
j
N
F
ma
fF
W
Pg 4
i
Modello per l’attrito di scorrimento
La direzione del vettore forza di attrito è perpendicolare al
vettore della forza normale N.
L’intensità della forza d’attrito |fF| è proporzionale all’intensità
della forza normale |N |.
|fF| = µK | N | ( = µK | W | nell’esempio precedente)
Più pesante è qualcosa, maggiore sarà l’attrito che farà!!
La costante µK è chiamata “Coefficiente di attrito dinamico.”
Pg 5
Modello...
Dinamica:
i:
j:
F − µKN = ma
N = mg
F − µK mg = ma
così
j
N
F
ma
µK mg
W
|W| =mg
Pg 6
i
Piano inclinato con attrito:
Tracciamo il diagramma delle forze:
ma
µKN
j
N θ
mg
θ
i
Pg 7
Piano inclinato...
Consideriamo le componenti i e j di
µKN
ma
j
FNET = ma
i
mg sin θ − µKN = ma
j
N = mg cos θ
mg sin θ − µK mg cos θ = ma
N θ
mg
i
θ
a / g = sin θ − µK cos θ
mg cos θ
mg sin θ
Pg 8
Attrito Statico...
Fino ad ora abbiamo considerato l’attrito che agisce quando
qualcosa si muove.
Sappiamo però che esso agisce anche sui sistemi statici :
In questi casi, la forza fornita dall’attrito dipenderà dalle forze
applicate sul sistema.
j
N
F
i
fF
W
|W| =mg
Pg 9
Attrito statico...
E’del tutto simile al caso dell’attrito di scorrimento con a = 0.
i:
F − fF = 0
j:
N = mg
Mentre il blocco è fermo: fF = F
j
N
F
i
fF
W
|W| =mg
Pg 10
Attrito Statico...
La massima forza possibile che l’attrito fra due oggetti può
fornire è fMAX = µSN, dove µs è il “coefficiente di attrito
statico.”
Così fF ≤ µS N.
Quando F cresce, fF diventa più grande fino a quando
fF = µSN e l’oggetto comincia a muoversi.
j
N
F
i
fF
W
|W| =mg
Pg 11
Attrito Statico...
µS è evidenziato dal crescere di F fino a quando il blocco non
inizia a scivolare:
i:
FMAX − µS N = 0
j:
N = mg
µS = FMAX / mg
j
N
FMAX
µS mg
i
W
|W| =mg
Pg 12
Attrito Statico :
Possiamo considerare anche µS su un piano inclinato.
θ
In questo caso, la forza fornita dall’attrito dipenderà dall’angolo θ del
piano.
Pg 13
Attrito Statico...
La forza fornita dall’attrito, fF , depende da θ.
fF
ma = 0
(il blocco è fermo)
mg sin θ − ff = 0
j
N θ
(II Legge di Newton lungo l’asse x)
mg
θ
i
Pg 14
Attrito Statico...
Possiamo trovare µs aumentando l’angolo della rampa fino a
quando il blocco non scivola:
mg sin θ − ff = 0
In this case:
ff = µSN = µSmg cos θM
µSN
mg sin θM − µSmg cos θM = 0
j
N
θM mg
θ
µS = tan θM
i
Pg 15
Commenti aggiuntivi sull’attrito:
Poichè fF = µN , la forza di attrito non dipende dall’area delle
superfici di contatto.
Per definizione deve essre vero che per qualunque sistema
µS > µK
Pg 16
Proprietà dell’attrito
Proprietà 1: Se il corpo non è in moto, la forza di attrito statico fs e
la componente di F parallela alla superficie hanno la stessa
intensità, e fs è diretta nella direzione della componente di F ma
in senso opposto.
Proprietà 2: L’intensità di fs può raggiungere un valore massimo
fs,max dato da
fs,max =µsN
Dove µs è il coefficiente di attrito statico e N l’intensità della forza
normale. Se l’intensità della componente di F parallela alla
superficie supera fs,max il corpo comincia a scivolare lungo la
superficie.
Proprietà 3:Se il corpo comincia a scivolare lungo la superficie,
l’intensità della forza di attrito decresce rapidamente fino al
valore fk dato da:
fk =µkN
Dove µk è il coefficiente di attrito dinamico.
Pg 17
A parte:
Grafico della forza di attrito in funzione della forza applicata
fF = µSN
fF = µKN
fF
fF = FA
FA
Pg 18