Variazione della Frequenza di Taglio

Luca Fortina
5TB
28/09/12
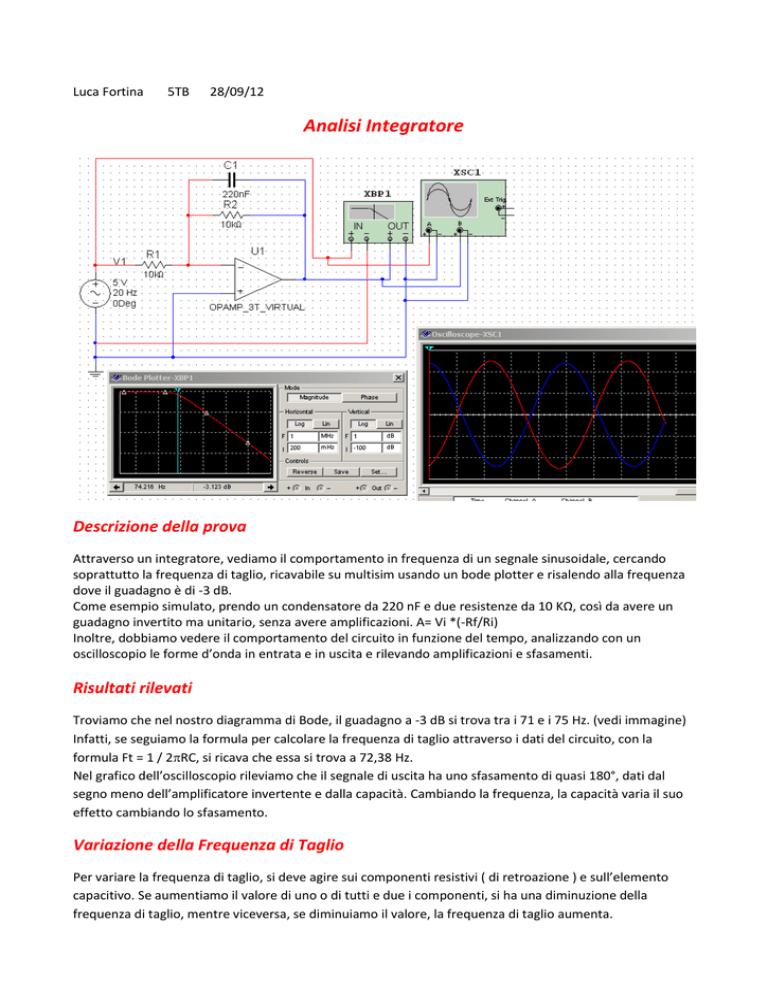
Analisi Integratore
Descrizione della prova
Attraverso un integratore, vediamo il comportamento in frequenza di un segnale sinusoidale, cercando
soprattutto la frequenza di taglio, ricavabile su multisim usando un bode plotter e risalendo alla frequenza
dove il guadagno è di -3 dB.
Come esempio simulato, prendo un condensatore da 220 nF e due resistenze da 10 KΩ, così da avere un
guadagno invertito ma unitario, senza avere amplificazioni. A= Vi *(-Rf/Ri)
Inoltre, dobbiamo vedere il comportamento del circuito in funzione del tempo, analizzando con un
oscilloscopio le forme d’onda in entrata e in uscita e rilevando amplificazioni e sfasamenti.
Risultati rilevati
Troviamo che nel nostro diagramma di Bode, il guadagno a -3 dB si trova tra i 71 e i 75 Hz. (vedi immagine)
Infatti, se seguiamo la formula per calcolare la frequenza di taglio attraverso i dati del circuito, con la
formula Ft = 1 / 2RC, si ricava che essa si trova a 72,38 Hz.
Nel grafico dell’oscilloscopio rileviamo che il segnale di uscita ha uno sfasamento di quasi 180°, dati dal
segno meno dell’amplificatore invertente e dalla capacità. Cambiando la frequenza, la capacità varia il suo
effetto cambiando lo sfasamento.
Variazione della Frequenza di Taglio
Per variare la frequenza di taglio, si deve agire sui componenti resistivi ( di retroazione ) e sull’elemento
capacitivo. Se aumentiamo il valore di uno o di tutti e due i componenti, si ha una diminuzione della
frequenza di taglio, mentre viceversa, se diminuiamo il valore, la frequenza di taglio aumenta.
Alcune prove con frequenze di taglio diverse, tramite la modificazione dei parametri Rf e C.
Prove a varie frequenze
A 100 Hz
A 500 Hz
A 100 Hz ( V. Figura) lo sfasamento è minore di 180°, ed è attenuata, a causa della frequenza che è fuori
dalla banda passante.
A 500 Hz ( V. Figura ) lo sfasamento è ancora minore di quanto è a 100 Hz ed è attenuatissima, a causa della
sempre più alta frequenza del segnale
Prova con Onda Quadra
Con un’onda quadra, a frequenze superiori della frequenza di taglio, il segnale in uscita viene tagliato e si
trasforma in un onda triangolare sfasata per l’effetto della capacità, come per l’onda sinusoidale, ma
questa trasformazione è data dalle diverse amplificazioni delle armoniche componenti l’onda quadra (
Teorema di Fourier ) a causa del superamento della frequenza di taglio.
Attraverso le prove ad altre frequenze, abbiamo visto che, quando la frequenza è dentro alla banda
passante il grafico in uscita rileva delle curve che possono essere imputate alla carica e alla scarica del
condensatore, che a basse frequenze ha ancora un comportamento come un circuito aperto.
A frequenze appena superiori alla frequenza di taglio, il grafico rileva che il condensatore fa sempre più
fatica a caricarsi e scaricarsi, cambiando la forma dell’onda.
Rileviamo che a frequenze sotto la Ft, l’onda ha forma vicina all’onda quadra in ingresso, mentre a
frequenza appena superiore a Ft, l’onda prende la forma “a dente di sega” e per frequenze molto più alte
della Ft si ha un’onda triangolare.
Prove ad altre frequenze
Prova a 20 Hz ( sotto frequenza di taglio)
Prova a 80 Hz ( appena superiore a frequenza di taglio )
Prova a 1440 kHz ( venti volte la frequenza di taglio )
Il lavoro denota una completa comprensione degli argomenti ed uno svolgimento accurato delle prove di
simulazione
Voto 9 (nove)
Franca Brusotti