LabCont1: Laboratorio di Controlli 1
II Trim. 2007
Lezione 1 — 17 Gennaio
Docente: Luca Schenato
1.1
Stesori: Luca Schenato
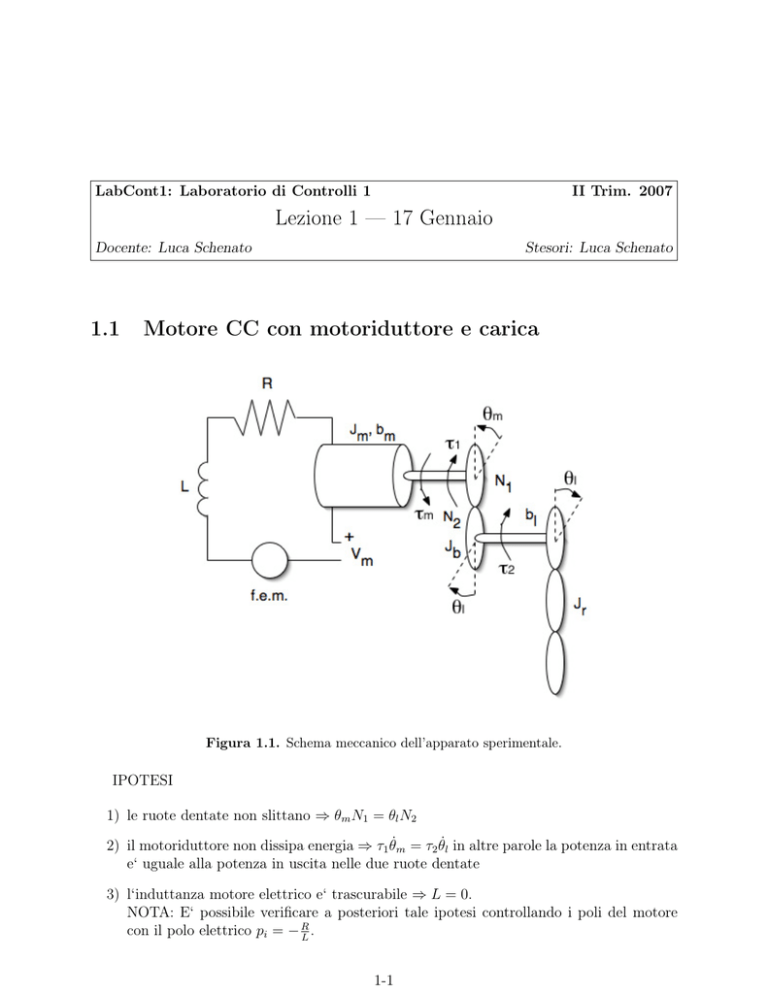
Motore CC con motoriduttore e carica
Figura 1.1. Schema meccanico dell’apparato sperimentale.
IPOTESI
1) le ruote dentate non slittano ⇒ θm N1 = θl N2
2) il motoriduttore non dissipa energia ⇒ τ1 θ̇m = τ2 θ̇l in altre parole la potenza in entrata
e‘ uguale alla potenza in uscita nelle due ruote dentate
3) l‘induttanza motore elettrico e‘ trascurabile ⇒ L = 0.
NOTA: E‘ possibile verificare a posteriori tale ipotesi controllando i poli del motore
con il polo elettrico pi = − R
.
L
1-1
LabCont1
Lezione 1 — 17 Gennaio
Parametro
Vm
τm
τ1
τ2 = τb
τl
θm
θl
bm
bl
Jm
Jb
Jl = m 2 l
m
l
Jr
N 1 = Nm
N 2 = Nl
II Trim. 2007
Descrizione
Tensione di ingresso al motore
Momento torcente applicato dal motore
Momento torcente reattivo sulle ruote del motore
Momento torcente applicato alla base del motoriduttore
Momento torcente reattivo dovuto al carico
Angolo del rotore del motore
Angolo della base del motore
Coefficiente d’attrito viscoso del motore
Coefficiente d’attrito viscoso della base
Momento d’inerzia del motore
Momento d’inerzia della base
Momento d’inerzia dovuto al carico
Massa del pendolo
distanza centro di massa del pendolo dal vincolo
Momento d’inerzia di una ruota dentata
Numero di denti della ruota dentata del motore
Numero di denti della ruota dentata della base
Tabella 1.1. Descrizione dei parametri del modello meccanico.
PARTE ELETTRICA DEL MOTORE
Vm = Ri + Kφ θ̇m
(1.1)
τ m = Kφ i
(1.2)
PARTE MECCANICA DEL MOTORE
Jm θ̈m = τm − bm θ̇m − τ1
(1.3)
(Jb + Jl )θ̈l = τb − bl θ̇l − mgl sin(θl )
(1.4)
Si noti che in quest‘ultima equazione Jl si somma a Jb dal momento che il pendolo e‘ attaccato rigidamente alla base e quindi contribuisce all‘inerzia.
1-2
LabCont1
Lezione 1 — 17 Gennaio
II Trim. 2007
OBIETTIVO
Trovare θl (s) = P (s)Vm (s), cioe’ la dinamica dell’angolo di uscita rispetto al controllo.
In tale equazione θl (s) svolge il ruolo di uscita y e Vm (s) il ruolo di ingresso u.
Sia
N=
Nl
.
Nm
Sostituiamo in (1.3) le equazioni θm = N θl e τ1 =
θ˙l
˙ τb
θm
=
Jm N θ̈l = τm − bm N θl −
1
τ
N b
ottenendo
τb
N
da cui
(Jm N 2 )θ̈l = N τm − (bm N 2 )θl − τb .
(1.5)
Sostituiamo τb ottenuto in (1.5) in (1.4) e otteniamo
(Jb + Jl )θ̈l = N τm − (bm N 2 )θl − (Jm N 2 )θ̈l − bl θ̇l − mgl sin(θl )
da cui
(Jl + Jb + N 2 Jm )θ̈l = −(bl + N 2 bm )θ̇l − mgl sin(θl ) + N τm .
(1.6)
Quest’ultima equazione rappresenta la dinamica della parte meccanica.
Notare che e’ possibile definire
4
Jeq = Jb + Jl + N 2 Jm
4
beq = bl + N 2 bm
4
eq
τm
= N τm
da cui
eq
Jeq θ̈l = −beq θ̇l − mgl sin θl + τm
.
(1.7)
Calcoliamo ora la dinamica della parte elettrica:
Vm = Ri + KΦ N θ̇l
τ m = KΦ i
Jeq θ̈l = −beq θ̇l − mgl sin θl + N τm
1-3
(1.8)
(1.9)
(1.10)
(1.11)
LabCont1
Lezione 1 — 17 Gennaio
II Trim. 2007
Figura 1.2. Modello in diagramma a blocchi.
CASI PARTICOLARI
(A) non c‘e‘ il pendolo dunque m = 0.
Jeq
beq
Kφeq
eq
τm
=
=
=
=
Jm N 2 + Jl
bl + N 2 bm
N Kφ
N τm
Abbiamo che
θl (s) = P (s)Vm (s)
da cui
P (s) =
K∗
N Kφ
=
Jeq RS + (Rbeq + N 2 Kφ2 )
s(s + p)
ove si e‘ posto
K∗ =
N Kφ
,
Jeq R
p=
Rbeq + N 2 Kφ2
.
Jeq R
Si noti che questo rappresenta il modello usuale per motore elettrico ove K ∗ e p sono
diversi.
1-4
LabCont1
Lezione 1 — 17 Gennaio
II Trim. 2007
Figura 1.3. Stesso modello di motore elettrico senza la base Uniche differenze sono il calcolo di Jeq , beq e
Kφeq .
(B) Supponiamo che i segnali in gioco siano piccoli. Dunque possiamo supporre ragionevole
l‘approssimazione sin θl ≈ θl . Sia
Vm = Ri + Keq θ̇l eq
= Kφeq i = KReq Vm − Kφeq θ̇l
τm
eq
Jeq θ̈l = −beq θ̇l − mglθl + τm
Da queste equazioni si ha che
Kφeq
φ
Jeq θ̈l = −beq θ̇l − mglθl +
Vm − Keq
R
da cui
φ
RJeq θ̈l = − Rbeq + (Kφeq )2 θ̇l − mglRθl + Keq
Vm
Dunque in termini di funzione di trasferimento abbiamo che
θl (s) = T (s)Vm (s)
ove
avendo posto
Kφeq
γ
= 2
T (s) =
eq 2
2
Jm Rs + (Rbeq + (Kφ ) )s + mglR
s + αs + β
Kφeq
γ=
,
Jm R
Rbeq + (Kφeq )2
α=
,
Jm R
β=
Si noti che T (s) rappresenta un sistema del secondo ordine.
1-5
mgl
Je q
LabCont1
Lezione 1 — 17 Gennaio
Figura 1.4. modello diagramma a blocchi
1.2
Motore in laboratorio
Figura 1.5. Vista laterale dell’apparato meccanico.
1-6
II Trim. 2007
LabCont1
Lezione 1 — 17 Gennaio
Figura 1.6. Vista superiore dell’apparato meccanico.
1.2.1
Parametri del motore
Parametro
kφ
kT
R
L
N
Jb
Jr
Jm
Valore
0.00767
1.63
2.6
0.18 ∗ 10−3
14
3 ∗ 10−5
1.4 ∗ 10−6
3.87 ∗ 10−7
Unità di misura
volt/(rad/sec)
volt/rad
Ω
H
kg ∗ m2
kg ∗ m2
kg ∗ m2
Tabella 1.2. Valori nominali del motore.
Dai dati riportati in tabella otteniamo:
Kφeq = N ∗ Kφ = 0.1074 [V olt/(rad/s)]
Je q = Jb + 3Jr + N 2 Jm = 1.1 ∗ 10−4 [kgm2 ]
bm , br =?? non sono noti, quindi devono essere stimati.
1-7
II Trim. 2007












