Lo schema AD-AS
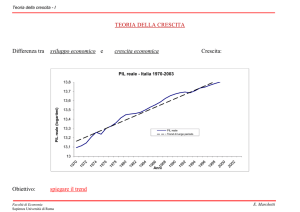
IL MODELLO AD – AS
Il livello dei prezzi P è ora una endogena.
Rimuoviamo l’ipotesi di prezzi fissi.
Nel modello IS – LM, il reddito di equilibrio era quello che soddisfaceva la domanda aggregata, tenuto conto
dell’influenza di i, cioè del mercato monetario.
Dunque:
YIS* − LM
=
quantità complessiva domandata di beni
Se consideriamo P come variabile endogena nell’IS – LM, otterremo una funzione di domanda aggregata (o
macroeconomica) di beni
1⎛
M
LM : i = ⎜ L −
P
h⎝
P↑
⇒
⎞ k
⎟+ Y
⎠ h
M
↓ ⇒ i↑
P
Facoltà di Economia
Sapienza Università di Roma
che effetto ha un aumento di P?
per ogni possibile livello di Y
La LM si sposta verso l’alto.
E. Marchetti
Lo schema AD-AS
i
Tre livelli crescenti:
LM2
LM1
P0 < P1 < P2
LM0
i*
i
IS
Y0
Y
P
AD
P2
P1
P0
Y2
Facoltà di Economia
Sapienza Università di Roma
Y1
Y0
Y
E. Marchetti
Lo schema AD-AS
Da:
⎧
1
[C + I − bi ]
⎪ IS : Y =
c
1
−
⎪⎪
⎨
⎪
1
M
k
⎪ LM : i = ⎛⎜ L − ⎞⎟ + Y
⎪⎩
h⎝
P⎠ h
Reddito eq. IS – LM,
cioè AD:
Y=
mb ⎛ M
mh
⎞
(C + I ) +
⎜ −L⎟
h + mbk⎝ P
h + mbk
⎠
Effetti di variazioni di alcune esogene, fermi restando i prezzi P:
P
P
aumento di
aumento di
I,C
L
AD’
AD
AD
AD’
Y
Y
P
aumento di
inclinazione AD:
M
dY
mb ⎛ M ⎞
=−
⎜
⎟
dP
m + mbk ⎝ P 2 ⎠
AD’
AD
Y
Facoltà di Economia
Sapienza Università di Roma
E. Marchetti
Lo schema AD-AS
Come determinare i livelli di equilibrio di Y e di P?
deriva dal comportamento delle imprese:
Manca una relazione:
Offerta aggregata (AS)
max. profitto
I) concorrenza perfetta
Due possibili configurazioni di mercato:
II) oligopolio (conc. imperfetta)
I) Concorrenza perfetta
Funzione di produzione:
Un fattore variabile – lavoro, il cui costo è:
max. profitto:
P = CMa
dN
= inverso della produttività
dY
marginale
Facoltà di Economia
Sapienza Università di Roma
Y = f (N )
WN
CMa =
dCT d (WN )
dN
=
=W
dY
dY
dY
P=
W
dY / dN
E. Marchetti
Lo schema AD-AS
dY
è decrescente rispetto al fattore (N)
dN
W
è crescente rispetto a Y.
quindi il costo marginale CMa =
dY / dN
la produttività marginale
P,
CMa
CMa
P1
P0
Y0
Facoltà di Economia
Sapienza Università di Roma
Y1
Y
E. Marchetti
Lo schema AD-AS
Mercato del lavoro:
aggregando le imprese:
dY W
=
dN P
W/P
curva di domanda di lavoro
⎛W ⎞
⎜ ⎟
⎝ P ⎠0
⎛W ⎞
⎜ ⎟
⎝ P ⎠1
dY
dN
N0
N
N1
Il salario nominale W è rigido (vari motivi: contrattazione, ecc.);
Se:
↑P
↓
⇒
W
P
Si riduce il
salario reale
↓
⇒
Cala la prod.
marginale del
lavoro
Mercato del lavoro
Facoltà di Economia
Sapienza Università di Roma
dY
dN
⇒
↑ CMa
Il costo
marginale può
aumentare
⇒ ↑ (Y , N )
Crescono occupati e
prodotto (offerta)
Mercato dei beni (offerta)
E. Marchetti
Lo schema AD-AS
Ad un salario reale
minore le imprese sono
disposte a assumere più
lavoro
Per la funzione di
produzione, più lavoro
implica più prodotto
P
W/P
AS
P1
W / P0
P0
W / P1
Y0
Y1
Y
N
Y
Y
dY/dN
Y = f (N )
45°
Y
Facoltà di Economia
Sapienza Università di Roma
N
E. Marchetti
Lo schema AD-AS
La curva AS è determinata da queste tre equazioni:
Y = f (N )
dY W
=
dN P
W =W
In effetti la curva AS emerge dalla struttura dei costi delle imprese e dalla massimizzazione del profitto:
curva costi marginali (CMa) = curva di offerta (AS)
Offerta AS:
Facoltà di Economia
Sapienza Università di Roma
Y = Y S (P)
con:
dY
>0
dP
E. Marchetti
Lo schema AD-AS
II) Oligopolio
Per un’impresa oligopolista: la produttività media e marginale sono costanti fino a un certo Y, poi decrescono
fissazione del prezzo tramite mark – up ( π ) sui costi medi variabili:
P = (1 + π )
WN
Y
= (1 + π )
W
q
q = produttività media del lavoro
P,
CMa
AS
Tratto di produttività
media/marg. costante
Tratto di produttività
media/marg. decrescente
Y0
Facoltà di Economia
Sapienza Università di Roma
Y1
Y
E. Marchetti
Lo schema AD-AS
Equilibrio di offerta e domanda aggregata
mS h
mS b
M
⎧
AD
:
Y
=
(
E
−
(
b
/
h
)
L
)
+
⋅
⎪
h + mS bk
h + mS bk P
⎪⎪
⎨
⎪
S
AS
:
Y
=
Y
( P)
⎪
⎪⎩
E = C + I + G + c(TR − T )
Il sistema determina Y* e P* di equilibrio.
P
AS
P*
AD
Y*
Facoltà di Economia
Sapienza Università di Roma
Y
E. Marchetti
Lo schema AD-AS
Statica comparata nel modello AS – AD:
es. instabilità delle aspettative sugli investimenti ( I ):
Teoria delle fluttuazioni basata sull’AD – AS
AS
P
AS
AD’
AD
P*
B
E*
AD
P**
E**
Y** Y*
Riduzione di I
( ΔI < 0 )
AD’
Y
E**
P**
P*
C
E*
Y*
Y**
Aumento di I
( ΔI > 0 )
Analoghi effetti si ottengono a seguito di variazioni della preferenza per la liquidità L .
Facoltà di Economia
Sapienza Università di Roma
E. Marchetti
Lo schema AD-AS
Y e N di equilibrio dipendono da domanda e offerta aggregata; possono entrambi essere inferiori al pieno impiego.
Es.
la domanda aggregata AD può essere troppo bassa:
Si può agire con la politica macro per stimolare la AD.
P
NOTA: la disoccupazione involontaria dovuta alla differenza
YP − Y * è in genere associata a qualche frizione sul mercato
del lavoro.
E*
P*
AS
AD
Y*
YP
Y
Corrisponde a disoccupazione
involontaria (NP – N* ) > 0
Potrebbero essere dunque i salari monetari W, ipotizzati rigidi, a creare la disoccupazione.
Facoltà di Economia
Sapienza Università di Roma
E. Marchetti
Lo schema AD-AS
Nell’originale modello AD – AS della sintesi, la subottimalità dell’equilibrio macro era infatti riconducibile alla rigidità
dei salari nominali.
AS
P
W/P
NS
Al salario nominale W , corrisponde un
salario reale maggiore di quello di
equilibrio walrasiano (W / P )P ,
W /P*
(W / P )
P*
P
dY/dN
AD
Y*
YP
Y
N*
e quindi una disoccupazione involontaria
pari a:
U = NP − N *
NP
U
Y
Y
Y = f(N)
45°
Y
Facoltà di Economia
Sapienza Università di Roma
N
E. Marchetti