Teoria della crescita - I
TEORIA DELLA CRESCITA
Differenza tra
sviluppo economico e
Crescita:
crescita economica
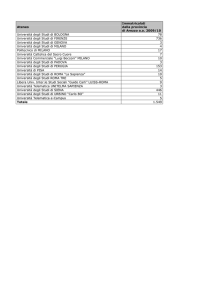
PIL reale - Italia 1970-2003
13,8
13,7
PIL reale (logaritmi)
13,6
13,5
13,4
13,3
PIL reale
Trend di lungo periodo
13,2
13,1
13
Anni
Obiettivo:
spiegare il trend
Facoltà di Economia
Sapienza Università di Roma
E. Marchetti
Teoria della crescita - I
La teoria della crescita neoclassica: il modello di Solow
Un solo bene omogeneo (approccio macro); economia chiusa; senza P.A.; concorrenza perfetta;
tempo continuo: alcune endogene variano in t in modo continuo.
4 mercati:
-
mercato dei beni: Y, C, I
mercato S – I
mercato del lavoro (offerta inelastica N al pieno impiego)
mercato del capitale K.
Funzione di produzione:
Yt = f ( Et ⋅ N t , K t )
dEt 1
⋅ = λ tasso di crescita del progresso tecnico
dt Et
Rendimenti costanti di scala:
dN t 1
⋅
= n tasso di crescita popolazione (off. lavoro)
dt N t
xYt = f ( x( Et ⋅ N t ), xK t )
poniamo: x =
Facoltà di Economia
Sapienza Università di Roma
Et = progresso tecnico labour augmenting
1
Et ⋅ N t
⇒
⎛
Yt
= f ⎜⎜1,
Et ⋅ N t
⎝
Kt
Et ⋅ N t
⎞
⎟⎟
⎠
E. Marchetti
Teoria della crescita - I
yt = φ ( k t )
Funzione di produzione in forma intensiva:
con: yt =
Yt
;
Et ⋅ N t
kt =
Kt
Et ⋅ N t
⇒
La funzione di produzione in forma intensiva conserva le proprietà della produttività marginale dei fattori:
d2y
<0
dk 2
dy
>0
dk
y
oppure:
φ ' (k ) > 0
φ ' ' (k ) < 0
y = φ (k )
tan a =
Nota:
y Y / EN Y
=
=
k K / EN K
inverso del rapporto capitale/prodotto
- lim φ ′(k ) = ∞
k →0
- lim φ ′(k ) = 0
k →∞
tan a
k
Facoltà di Economia
Sapienza Università di Roma
E. Marchetti
Teoria della crescita - I
Accumulazione:
d (K / EN )
=
dt
Ma risulta:
Cioè:
dK t
= I t − δK t
dt
In termini intensivi:
dK 1
dN K
−
−
dt EN
dt E ( N )2
dk
dK 1
=
− nk − λk
dt
dt EN
Quindi, in termini intesivi:
dE K
dt N (E )2
dK 1
dk
=
+ nk + λk
dt EN
dt
dkt
= it − (n + λ + δ )kt
dt
Risparmio = quota costante del reddito:
st = syt = sφ (kt )
Per cui:
dkt
= sφ (kt ) − (n + λ + δ )kt
dt
In steady state k non varia nel tempo: dkt/dt = 0
Facoltà di Economia
Sapienza Università di Roma
dK t 1
= it − δkt
dt Et N t
Equilibrio
da cui:
I = S:
it = sφ (kt )
sφ (k *) = (n + λ + δ )k *
E. Marchetti
Teoria della crescita - I
Graficamente:
nello steady state (o stato stazionario) y, i, k sono costanti nel tempo
φ (k )
y, i
(n + λ + δ )k
s ⋅ φ (k )
Il sistema finirà inevitabilmente nello stato stazionario
kt = k * ∀t
Si consideri l’equazione differenziale che descrive
l’evoluzione di k nel tempo in equilibrio:
dkt
= sφ (kt ) − (n + λ + δ )kt
dt
k*
k
Possiamo considerare
espressa da:
dkt
dt
come una funzione di k
sφ (kt ) − (n + λ + δ )kt ;
Graficamente la relazione tra
Facoltà di Economia
Sapienza Università di Roma
dkt
dt
e
sφ (kt ) − (n + λ + δ )kt
è espressa dal
diagramma di fase:
E. Marchetti
Teoria della crescita - I
La forma di
sφ (kt ) − (n + λ + δ )kt
è data dall’andamento di φ ′ :
la derivata è:
sφ ′(k ) − (n + λ + δ )
meccanismo economico
dkt
dt
i mercati dei fattori sono in concorrenza perfetta:
∂f
rt =
= φ ′(kt )
∂K t
k*
kt
φ ′(k ) alta
Se k < k * ⇒
alto ⇒ k cresce
⇒
r alto
φ ′(k ) bassa
Se k > k * ⇒
basso ⇒ k cala
⇒
r basso ⇒ i
⇒
sφ (kt ) − (n + λ + δ )kt
In stato uniforme ( kt = k * ), tutte le variabili endogene (Y, K, I.) crescono allo stesso tasso:
poiché
K
è costante le proporzioni non cambiano sentiero di crescita bilanciata:
EN
Facoltà di Economia
Sapienza Università di Roma
gn = n + λ
Y
K
e
N
N
crescono al tasso λ
E. Marchetti
i
Teoria della crescita - I
Effetti di un aumento della propensione marginale al risparmio s:
(n + λ + δ )k
y, i
s '⋅φ (k )
A
s ⋅ φ (k )
nuovo stato stazionario: k**
k*
k**
k
In A il risparmio s ′φ (k *) è ora aumentato: ⇒ aumenta i,s ⇒ cresce k ⇒ si arriva a k** (e k lì si ferma…)
Risultato finale:
Facoltà di Economia
Sapienza Università di Roma
k è aumentato ma g n è rimasto invariato
Per far variare g n devono cambiare n o λ .
E. Marchetti
Teoria della crescita - I
Confronto con i fatti stilizzati:
Il modello di Solow spiega questi fatti stilizzati della crescita:
- il rapporto K/Y è all’incirca costante;
- tasso di crescita di Y e di K maggiori di n;
- le quote di reddito che vanno ai fattori (capitale e lavoro) restano costanti…
ma non riesce a spiegare questi:
- se λ è esogeno, allora tutti i paesi dovrebbero nel lungo periodo sperimentare tassi di crescita di Y/N simili: ciò
non accade…
- siccome Y/N è maggiore nei paesi sviluppati, questi dovrebbero avere anche un maggior K/N; questo è vero,
ma nella realtà il divario tra OCSE e PVS nel rapporto K/N è troppo basso per spiegare empiricamente la
differenza in Y/N;
o es.: (Y/NUSA) / (Y/NIndia) = 14,7 (1951-2004)
allora con α =0,33
(K/NUSA) / (K/NIndia) = 1000 !
- se (K/NOCSE) > (K/NPVS) allora dovrebbe essere: rOCSE < rPVS e il capitale dovrebbe fluire dai paesi
sviluppati a quelli in via di sviluppo; queste differenze nei tassi r, così come i flussi di capitale, sono troppo
limitate nella realtà…
Facoltà di Economia
Sapienza Università di Roma
E. Marchetti