LA PERCENTUALE
La percentuale è un modo di esprimere il rapporto tra 2 grandezze e viene indicata con il simbolo %.
La scrittura “ 30 % “ si legge “ 30 per cento” e rappresenta la percentuale mentre il numero 30 è il
tasso percentuale.
La percentuale corrisponde ad un rapporto in cui il denominatore è uguale a 100.
ESEMPI:
30
50
12
30 %=
=0,3 ;
50 %=
=0,5 ; 12 %=
=0,12 ecc.....
100
100
100
CALCOLO DELLA LA PERCENTUALE
Essendo un rapporto, per cacolare la percentuale di una certa quantità si procede esattamente come
fatto finora con le frazioni.
ESEMPIO: In un negozio leggiamo che il prezzo di un vestito è di 250 € ma sul prezzo c'è uno sconto
del 30%. Quanto vale lo sconto?
Sconto = 30% x 250 € =
30
30×250 €
×250 €=
=75 €
100
100
TRASFORMARE UN RAPPORTO IN PERCENTUALE
Tutti i rapporti possono essere espressi sottoforma di percentuale.
ESEMPIO: In una classe di 24 alunni, 6 hanno gli occhi chiari.
Qual è il rapporto tra gli alunni con gli occhi chiari e il numero totale di alunni? A che percentuale
corrisponde questo rapporto.
6
Il rapporto cercato è
e per esprimerlo in percentuale basta trasformarlo nella frazione decimale
24
equivalente (con denominatore uguale a 100):
6
25
=0,25=
=25 %
24
100
NOTA: possiamo ottenere lo stesso risultato usando le proporzioni, infatti stiamo cercando un
rapporto equivalente che quindi è in proporzione con quello di partenza. Quindi possiamo scrivere:
6 : 24 = x : 100
→ x = 6 x 100 = 25
24
; x rappresenta il tasso percentuale incognito da calcolare
LA RAPPRESENTAZIONE DEI DATI
TABELLA DI FREQUENZA
La frequenza assoluta o semplicemente frequenza di un dato è il numero di volte in cui il dato si
presenta. La frequenza relativa è il rapporto tra la frequenza e il numero totale di dati rilevati e si può
esprimere sottoforma di rapporto o di percentuale.
ESEMPIO:
Da una indagine sullo sport praticato da 25 ragazzi si sono ottenuti i seguenti dati:
calcio, tennis, tennis, pallavolo, calcio, calcio, basket, calcio, ciclismo, tennis, nuoto, calcio, nuoto,
ciclismo, calcio, basket, basket, nuoto, calcio, tennis, pallavolo, pallavolo,calcio, basket, tennis.
Il calcio ha frequenza 8 perchè compare 8 volte, il tennis 5, il basket 4 e così via..... La frequenza
8
=0,32=32 %
relativa del dato calcio è rappresentata dal rapporto
25
Le frequenze possono essere rappresentate in una tabella di frequenza in cui vengono riportati il tipo
di dato raccolto, in questo caso lo sport praticato, e la frequenza del dato.
→ La somma delle frequenze è uguale numero totale di dati raccolti
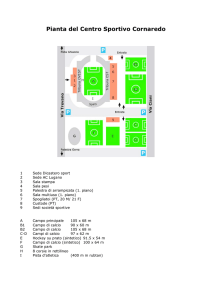
Sport
praticato
Calcio
Frequenza
8
(n di ragazzi)
Tennis
Basket
Nuoto
Pallavolo
Ciclismo
5
4
3
3
2
ISTOGRAMMA
L'istogramma è un grafico nel piano cartesiano formato da rettangoli affiancati. I rettangoli hanno la
stessa ampiezza di base mentre l'altezza corrisponde alla frequenza del dato rappresentato.
In ogni rettangolo vanno conteggiati tutti i dati compresi nell'intervallo stabilito per la base.
ESEMPIO:
L'istogramma nell'immagine rappresenta
la frequenza dei pesi misurati in un gruppo
di 23 ragazzi. L'ampiezza di base scelta
per i rettangoli è di 5kg.
La frequenza del primo rettangolo è 2 quindi ci sono
2 ragazzi il cui peso è maggiore o uguale a 55 kg e
minore di 60kg. La frequenza del secondo rettangolo è
5 quindi ci sono 5 ragazzi il cui peso è maggiore
o uguale a 60 kg e minore di 65 kg e così via...
Il primo valore dell'ampiezza di base è
incluso e l'ultimo è escluso.
Anche in questo caso naturalmente la
somma di tutte le frequenze è uguale al numero totale
di dati raccolti.
AREOGRAMMA
L'areogramma è un grafico formato da un cerchio diviso in settori circolari. Ogni settore corrisponde a
un certo dato e l'area del settore rappresenta la frequenza relativa del dato cioè a che percentuale
corrisponde il dato rispetto al totale. Ricordando che l'area del settore e il suo angolo al centro sono
grandezze direttamente proporzionali, per calcolare l'angolo del settore si usa la proporzione:
frequenza del dato : numero totale di dati = angolo settore : 360°
↓
angolo settore = frequenza del dato x 360° = frequenza relativa del dato x 360°
numero totale di dati
Nel secondo passaggio abbiamo semplicemente ricordato che la frequenza relativa =
Naturalmente la somma degli angoli dei vari settori deve essere uguale a 360°.
frequenza
numero di dati
ESEMPIO:
L'areogramma in figura rappresenta il
risultato dell'indagine sul modo in cui
450 ragazzi raggiungono la propria scuola.
Dall'indagine è risultato che 101 ragazzi
usano la bicicletta, 113 ragazzi vanno a
piedi mentre i rimanenti 236 usano l'auto.
Calcoliamo l'ampiezza degli angoli dei
settori corrispondenti ai tre tipi di
trasporti.
Angolo settore bicicletta (arancione) = frequenza bicicletta x 360°= 101 x 360° = 80,8° ≈ 81°
numero totale dati
450
Angolo settore a piedi (viola chiaro) = frequenza a piedi x 360°= 113 x 360° = 90,4° ≈ 90°
numero totale dati
450
Angolo settore auto(viola) = frequenza auto x 360°= 236 x 360° = 188,8° ≈ 189°
numero totale dati
450
I risultati vengono approssimati al grado in modo da poter essere disegnati facilmente con il
goniometro.