Condensatori e induttori

Condensatore
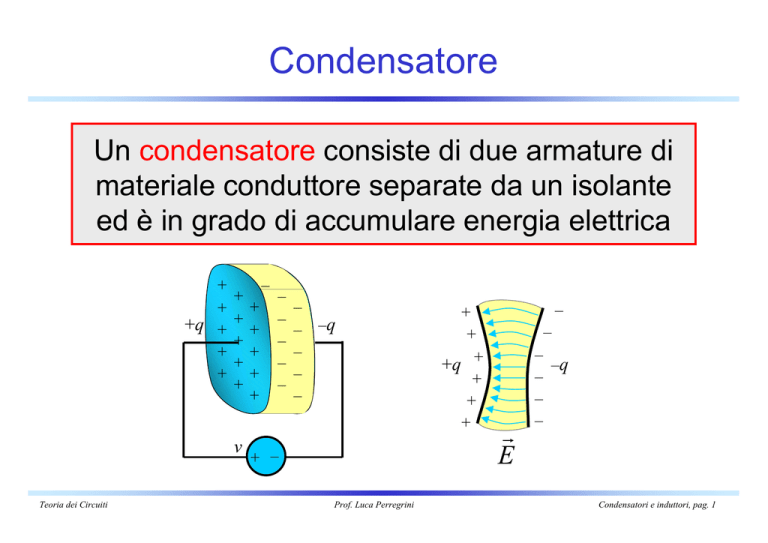
Un condensatore consiste di due armature di
materiale conduttore separate da un isolante
ed è in grado di accumulare energia elettrica
+
+
+q +
+
+
+
+
+
+
+
v
Teoria dei Circuiti
–
+
+
+
+
+
–
–
–
–
–
–
–
–
–
–
–q
+ –
Prof. Luca Perregrini
+
+
+q +
+
+
+
–
–
r
E
–
–q
–
–
–
Condensatori e induttori, pag. 1
Condensatore: relazione tensione/carica
La carica sulle armature è proporzionale alla
tensione ai loro capi attraverso il valore di capacità
del condensatore che si misura in Farad (F)
+
+
+q +
+
+
+
+
+
+
+
v
Teoria dei Circuiti
–
+
+
+
+
+
–
–
–
–
–
–
–
–
–
–
–q
q = C ⋅v
1 F = 1 C/V = 1 A·s/V
+ –
Prof. Luca Perregrini
Condensatori e induttori, pag. 2
Condensatore a piani paralleli
d
costante dielettrica ε
area A
+
+
+q +
+
+
+
+
+
+
+
v
–
+
+
+
+
+
–
–
–
–
–
–
–
–
–
–
+
+
+q +
+
+
+
–q
+ –
r
E
–
–
–
–q
–
–
–
A
C =ε ⋅
d
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 3
Condensatore: relazione tensione/corrente
dq d (C ⋅ v)
dv
i=
=
=C⋅
dt
dt
dt
i
C
+
v
–
Teoria dei Circuiti
(con la convenzione degli utilizzatori)
t
1
v(t ) = ∫ i (t ) dt + v(t0 )
C t0
Prof. Luca Perregrini
Condensatori e induttori, pag. 4
Condensatore: relazione tensione/corrente
i+
v
–
C
t
1
v(t ) = ∫ i (t ) dt + v(t0 )
C t0
dv
i =C⋅
dt
v
i
v
i
t
Teoria dei Circuiti
Prof. Luca Perregrini
i=∞
t
Condensatori e induttori, pag. 5
Condensatore in regime stazionario
i+
v
–
C
dv
i =C⋅
dt
v costante nel tempo
i
C
Teoria dei Circuiti
i = 0 (circuito aperto)
i=0
+
v
–
+
v
–
Prof. Luca Perregrini
Condensatori e induttori, pag. 6
Condensatore: potenza ed energia
dv
p = v ⋅i = C ⋅v ⋅
dt
t
t
t
dv
w = ∫ p(t ) dt = C ∫ v ⋅ dt = C ∫ v dv =
dt
−∞
−∞
−∞
t
2
1
1
q
2
2
= C ⋅v
= C ⋅v =
2
2
2C
−∞
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 7
Condensatori in serie
i
v
t
+
–
C1
CN
+ v –
1
+ v –
N
t
t
1
1
1
v = ∫ i dt + v1 (t0 ) +
i dt + v2 (t0 ) + K +
i dt + vN (t0 ) =
∫
∫
C1 t0
C2 t0
C N t0
t
t
 1

1
1
1
 ∫ i dt + v1 (t0 ) + v2 (t0 ) + K + vN (t0 ) =
=  +
+K+
i dt + v(t0 )
∫
C N  t0
Ceq t0
 C1 C2
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 8
Condensatori in serie
i
v
a
+
–
C1
CN
+ v –
1
+ v –
N
b
i
v
a
Ceq
+ v –
+
–
b
1
1
1
1
=
+
+K+
Ceq C1 C2
CN
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 9
Condensatori in parallelo
i
v
a
iN
i1
+
–
C1
CN
b
i = C1 ⋅
Teoria dei Circuiti
dv
dv
dv
dv
dv
+ C2 ⋅ + K + C N ⋅ = (C1 + C2 + K + C N ) ⋅ = Ceq ⋅
dt
dt
dt
dt
dt
Prof. Luca Perregrini
Condensatori e induttori, pag. 10
Condensatori in parallelo
i
v
a
i
iN
i1
+
–
C1
CN
v
b
a
i
+
–
Ceq
b
Ceq = C1 + C2 + K + C N
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 11
Induttore
Un induttore consiste di un filo (tipicamente
avvolto in più spire) percorso da corrente ed è
in grado di accumulare energia magnetica
i
r
B
+
v
–
i
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 12
Induttore: relazione flusso/corrente
Il flusso del campo magnetico è proporzionale alla
corrente attraverso il valore di induttanza
dell’induttore che si misura in Henry (H)
r
n
r
B
i
Φ = L ⋅i
+
v
–
r r
Φ = ∫ B • n dS
1 H = 1 V·s/A
S
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 13
Induttore a bobina
permeabilità magnetica µ
d
2
N A
L= µ⋅
d
N spire
Teoria dei Circuiti
area A
Prof. Luca Perregrini
Condensatori e induttori, pag. 14
Induttore: relazione tensione/corrente
di
dΦ d ( L ⋅ i )
v=
=
= L⋅
dt
dt
dt
i
L
+
v
–
Teoria dei Circuiti
(con la convenzione degli utilizzatori)
t
1
i (t ) = ∫ v(t ) dt + i (t0 )
L t0
Prof. Luca Perregrini
Condensatori e induttori, pag. 15
Induttore: relazione tensione/corrente
i +
v
–
L
di
v = L⋅
dt
i
v
1
i (t ) = ∫ v(t ) dt + i (t0 )
L t0
i
v
t
Teoria dei Circuiti
t
Prof. Luca Perregrini
v=∞
t
Condensatori e induttori, pag. 16
Induttore in regime stazionario
i +
v
–
L
di
v = L⋅
dt
i costante nel tempo
v = 0 (corto circuito)
i
i
L
Teoria dei Circuiti
+
v
–
+
v=0
–
Prof. Luca Perregrini
Condensatori e induttori, pag. 17
Induttore: potenza ed energia
di
p = v ⋅i = L ⋅ ⋅i
dt
t
t
t
di
w = ∫ p(t ) dt = L ∫ i ⋅ dt = L ∫ i di =
dt
−∞
−∞
−∞
t
1
1
2
2
= L ⋅i
= L ⋅i
2
2
−∞
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 18
Induttori in serie
i
v
v = L1 ⋅
Teoria dei Circuiti
+
–
L1
LN
+ v –
1
+ v –
N
di
di
di
di
di
+ L2 ⋅ + K + LN ⋅ = (L1 + L2 + K + LN ) ⋅ = Leq ⋅
dt
dt
dt
dt
dt
Prof. Luca Perregrini
Condensatori e induttori, pag. 19
Induttori in serie
i
v
a
+
–
L1
LN
+ v –
1
+ v –
N
b
i
v
a
Leq
+ v –
+
–
b
Leq = L1 + L2 + K + LN
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 20
Induttori in parallelo
i
v
a
iN
i1
+
–
L1
LN
b
t
t
t
1
1
1
i = ∫ v dt + i1 (t0 ) + ∫ v dt + i2 (t0 ) + K +
v dt + iN (t0 ) =
∫
L1 t0
L2 t0
LN t0
t
t
1 1

1
1
 ∫ v dt + i1 (t0 ) + i2 (t0 ) + K + iN (t0 ) =
=  + + K +
v dt + i (t0 )
∫
LN  t0
Leq t0
 L1 L2
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 21
Induttori in parallelo
i
v
a
i
iN
i1
+
–
L1
LN
v
b
a
i
+
–
Leq
b
1
1 1
1
= + +K+
Leq L1 L2
LN
Teoria dei Circuiti
Prof. Luca Perregrini
Condensatori e induttori, pag. 22