Sulla risoluzione dei problemi sulla forza di attrito statico

Sulla risoluzione dei problemi sulla forza di attrito statico
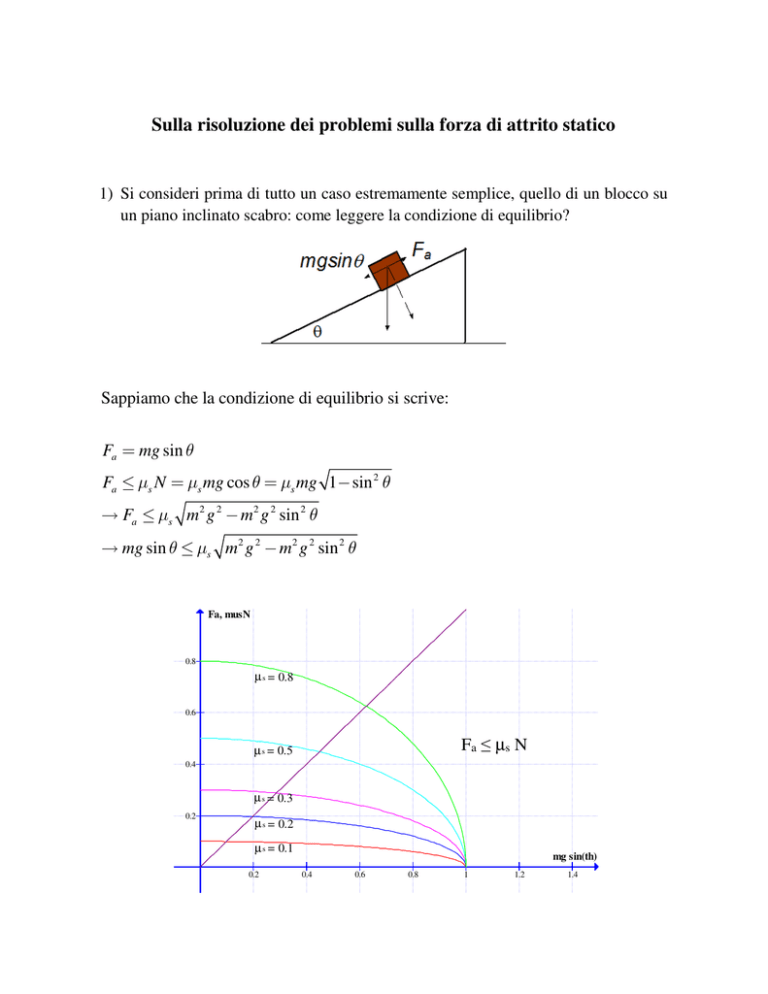
1) Si consideri prima di tutto un caso estremamente semplice, quello di un blocco su
un piano inclinato scabro: come leggere la condizione di equilibrio?
Sappiamo che la condizione di equilibrio si scrive:
Fa = mg sin θ
Fa ≤ µs N = µs mg cos θ = µs mg 1− sin 2 θ
→ Fa ≤ µs m 2 g 2 − m 2 g 2 sin 2 θ
→ mg sin θ ≤ µs m 2 g 2 − m 2 g 2 sin 2 θ
Fa, musN
0.8
µ s = 0.8
0.6
Fa ≤ µs N
µ s = 0.5
0.4
µ s = 0.3
0.2
µ s = 0.2
µ s = 0.1
0.2
mg sin(th)
0.4
0.6
0.8
1
1.2
1.4
La figura mostra come la condizione venga realizzata: la retta a 450 che passa per
l’origine rappresenta il valore della forza di attrito statico in funzione di mgsinθ, la
componente parallela al piano inclinato della forza di gravita’ ( ‘ forza motrice’),
quando il blocco e’ in equilibrio statico; si e’ scelto per comodita’ mg=1. Le curve
colorate rappresentano il valore µsN, che e’ il valore max Famax della forza di attrito
statico secondo la formula empirica di Coulomb, sempre in funzione della
componente di cui sopra. Si vede che per ogni valore di µs c’e’ un range di angoli fra
0 e θmax in cui Fa ≤Famax e il blocco e’ in equilibrio. Si vede anche che, per un dato
angolo del piano inclinato, la condizione di blocco in quiete non determina µs: si
puo’ solo stabilire qual e’ il valore minimo di µs necessario per l’equilibrio.
2) Si consideri ora un sistema leggermente piu’ complicato:
In questo caso non sappiamo a priori se, all’equilibrio, il verso della forza di attrito
statico e’ concorde o discorde con quello della componente della forza di gravita’
parallela al piano inclinato: dobbiamo quindi considerare separatamente i due casi.
TA − mA g sin θ = Fa
Attrito concorde a forza di gravita'
→ TA − mA g sin θ ≤ µs mA g cos θ
mB aB = mB g − TB = 0
TB = 2TA puleggia D
→ TB = mB g → TA =
mB g
2
mB g
− mA g sin θ ≤ µs mA g cos θ = µs mA g 1− sin 2 θ
2
 mB
m g

1
sin θ 
 ≈ 0.35
→ µs ≥  B − mA g sin θ 
= 
−
 2
 mA g cos θ  2mA cos θ cos θ 
→
µs e’ il valore minimo necessario a garantire l’equilibrio statico al blocco; il valore
numerico ≈ 0.35 corrisponde al caso θ= 300, mB =1.6 mA
TA − mA g sin θ = −Fa ≥ −µs mA g cos θ
Attrito concorde a tensione fune
mB aB = mB g − TB = 0
TB = 2TA puleggia D
→ TB = mB g → TA =
mB g
2
mB g
− mA g sin θ ≥ −µs mA g cos θ = −µs m A g 1− sin 2 θ
2
m g
→ − B + mA g sin θ ≤ µs mA g 1− sin 2 θ
2

 m g

1
mB
sin θ 
 ≈ −0.35 non fisico
= −
+
→ µs ≥ − B + mA g sin θ 

 mA g cos θ  2mA cos θ cos θ 
2
→
Fa, musN
0.8
0.6
Fa ≤ µs N
0.4
0.2
mg sin(th)
0.1
-0.2
0.2
0.3
µ s = 0.1
µ s = 0.2
µ s = 0.3
-0.4
µ s = 0.5
-0.6
-0.8
µ s = 0.8
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4