Funzione di rete
Cambio di punto di vista
ω variabile
Vs
1
X C = X C (ω ) = −
ωC
X L = X L (ω ) = ωL
Vu
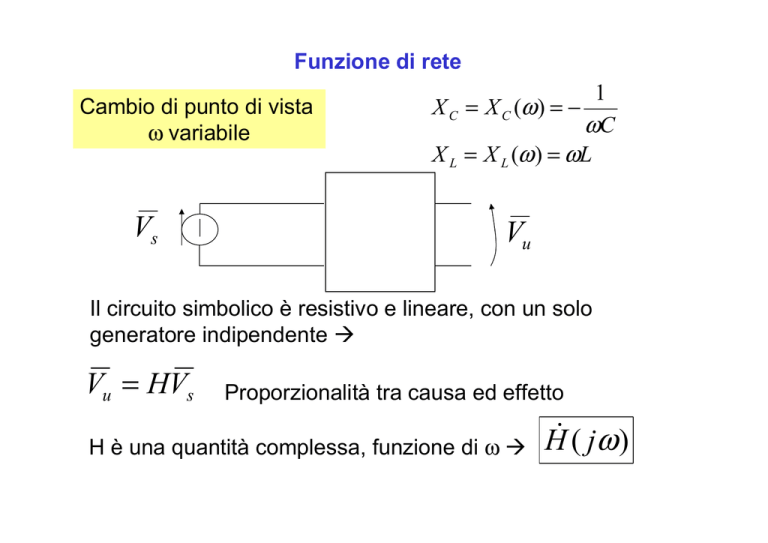
Il circuito simbolico è resistivo e lineare, con un solo
generatore indipendente Vu = HVs
Proporzionalità tra causa ed effetto
H è una quantità complessa, funzione di ω HC ( jω )
x(t )
Dominio
t
y (t )
Funzione di rete
X ( jω )
Dominio
f
Y ( jω )
Y ( jω )
H ( jω ) =
X ( jω )
•La funzione di rete descrive il comportamento del circuito al variare della
frequenza di ingresso
•E’ definita nel dominio della frequenza
•E’ il rapporto fra il fasore corrispondente alla sinusoide di uscita e il fasore
corrispondente alla sinusoide di ingresso
•Impedenza di trasferimento
•Rapporto di trasferimento in corrente
•Rapporto di trasferimento in tensione
•Ammettenza di trasferimento
•Impedenza d’ingresso
•Ammettenza di ingresso
[Ω]
[S]
[Ω]
[S]
0gni funzione di rete può essere scritta come rapporto di
polinomi nella variabile jω
bm ( jω ) + bm −1 ( jω ) + ... + b1 ( jω ) + b0
H ( jω ) =
m
m −1
am ( jω ) + am −1 ( jω ) + ... + a1 ( jω ) + a0
m
m −1
ak , bk ∈ ℜ
H è una funzione razionale reale della variabile jω
Risposta in frequenza
Funzione di rete
H = H ( jω ) =
Y ( jω )
H ( jω ) =
X ( jω )
.
Y ( jω )
Risposta in ampiezza
X ( jω )
fase(H ( jω )) = fase(Y ( jω )) − fase( X ( jω ))
Risposta in fase
L’insieme delle espressioni che danno il guadagno e lo sfasamento in
funzione della frequenza si chiama Risposta in frequenza
H max
H (ωc ) =
≅ 0.7 H max
2
ωc pulsazione di taglio
Vs
Vu
Vu = H Vs
Vu = Vu e jφu ; Vs = Vs e jφs ; H = H ( jω )e jφ (ω )
Vu e
jφu
jφ s
= Vs e H ( jω )e
jφ ( ω )
→ Vu = Vs H ( jω ); φu = φs + φ (ω )
vs (t ) = Vs cos (ωt + φs )
→ vu (t ) = Vu cos (ωt + φu ) = Vs H ( jω )cos (ωt + φs + φu )
L’effetto del circuito sul segnale di ingresso:
•una variazione dell’ampiezza di H(jω)
•una variazione di fase di φ(ω)
Si possono tracciare i grafici della risposta in frequenza utilizzando
scale logaritmiche :
DIAGRAMMI DI BODE
Guadagno in scala logaritmica = 20 log10 H (dB)
Diagramma di Bode per
HH = (1 + jω /ω 0)− 1.
La linea tratteggiata è la
curva esatta
dell’ampiezza.
La linea continua è
l’approssimazione
asintotica.
La risonanza
Fenomeno che accomuna molte scienze fisiche
Picco pronunciato nella risposta in ampiezza per un dato valore della frequenza
Coppia di poli complessi coniugati che provocano oscillazioni dell’energia
immagazzinata da una forma all’altra (L,C).
Circuito
RLC
V
Funzione di rete =
= Z (ω ) = R(ω ) + jX (ω )
I
> 0
Al variare di ω, può essere X (ω )= 0
< 0
Per ω = ω0 (ω0 pulsazione di risonanza) l’impedenza e’
puramente resistiva:
Z(ω0)=R, X(ω0)=0
I
R
Vg
Circuito risonante serie
jωL
1/jωC
I
1
1
1
H (ω ) = Y =
= =
=
1
Vg Z R + jωL − 1
R + j ωL −
jω C
ωC
1
ωL −
1
ωC
Z = R 2 + (ωL −
) 2 ∠ tan −1
R
ωC
1
1
⇒Z =R
ωL =
, → ω0 =
ωC
LC
1
ω0 =
rad/s Pulsazione di risonanza
LC
| Z |
X (ω ) = 0 ⇒ ωC −
ωL
ω0
per ω = ω0 =
ω
per ω = 0
per ω → ∞
-1/ ωC
π
ϕ
2
ϖ
−π
2
1
= 0 ⇒ ω0 =
ωL
1
LC
1
LC
Z =R ϕ =0
π
Z =∞ ϕ =−
2
π
Z → ωL ϕ =
2
Alla risonanza l’impedenza è reale e vale R. I =
Vg
R
Il modulo di Z è minimo il modulo della corrente è massimo
La serie LC ha impedenza nulla, quindi equivale ad un corto
circuito.
ω0 L
VC + VL = 0 VL = −VC = jω0 LI = j
Vg = jQVg
R
ω0 L
1
1
=
Q=
ω0 L =
Fattore di qualità
ω0C
ω0CR
R
VL = VC = Q Vg
Quando Q assume valori elevati, vL(t) e vC(t) assumono
ampiezze maggiori di quella del generatore problemi di
sovratensioni.
1 2
w
=
LI
L’energia immagazzinata nel circuito è costante
0
2
Infatti il parallelo LC è isolato dal resto del circuito.
Circuito risonante parallelo
Ig
R
L
C
V
1
1
1
C
C
= =
=
H (ω ) = Z =
1
1
1
1
Ig Y
+
+IC jωC
+ j ωC −
R jωL
R
ωL
g
2
1
1
1
−1
+ ωC −
Y=
∠ tan R ωC −
2
R
ωL
ωL
1
ω0 =
LC
| YC |
B(ω ) = 0 ⇒ ωC −
ωC
per ω = ω0 =
ω0
ω
per ω → ∞
1/ ωL
π
ϕ
2
ϖ
−π
2
per ω = 0
1
= 0 ⇒ ω0 =
ωL
1
LC
Y = 1/ R ϕ = 0
π
ϕ =−
2
π
C
Y → ωC ϕ =
2
YC = ∞
1
LC
Alla risonanza l’ammettenza è reale e vale 1/R. V = I g R
Il modulo di Y è minimo il modulo della tensione è massimo
Il parallelo LC ha ammettenza nulla, quindi equivale ad un circuito
aperto.
− jI g R
V
R
IC + I L = 0 I L = −IC =
=
=−j
I g = − jQI g
ω0 L
ω0 L
jω 0 L
R
Q=
= ω0CR
ω0 L
Fattore di qualità
I L = IC = Q I g
Se Q assume valori elevati iL(t) e iC(t) assumono ampiezze
maggiori di quella del generatore problemi di sovracorrenti
Fattore di qualità (o di merito)
Circuito RLC serie
ω0 L
1
1 L
Q=
=
=
ω0 RC R C
R
L' impedenza puo' essere scritta :
ω ω0
1
ω0 L ω ω 0
C
− = R 1 + jQ −
) = R 1 + j
Z = R + j (ωL −
ωC
R ω0 ω
ω0 ω
1
I
C
=
Y= =
C
Z Vg
G
ω ω0
1 + jQ −
ω0 ω
Ricalca l’andamento della corrente
Al variare del fattore di merito varia l’andamento della Y e
quindi della corrente.
ω1 e ω2 sono le pulsazioni di taglio, in corrispondenza delle quali:
ω ω0
Y ( jω2 ) Y ( jω1 )
1
=
=
⇒ Q − = ±1
G
G
2
ω0 ω
prendendo, delle 4 soluzioni, quelle positive :
ω1,2
1
1
= ω0 1 +
±
2
4
Q
2
Q
ω1ω2 = ω02 → ω0 = ω1ω2
Le pulsazioni di taglio non sono simmetrich e rispetto a ω0 .
ω0
→ si possono considerare simmetrich e
2Q
ω0
= B Ampiezza di Banda
ω1 − ω2 =
Q
Fissato ω0 , tanto piu' elevato e' Q tanto piu' stretta e' B.
H (jω) dB = 20 log10 H (jω)
ω1, 2 ≅ ω0 ±
1
→ 3dB
2
Ymax= G
I
I
Q>5
max
max
ω
ω
ω
Banda passante
ω1 Frequenza di taglio inferiore
ω2 Frequenza di taglio superiore
I
(Y)
Frequenza, rad/s
Per Q elevati, la Resistenza è attraversata da una corrente
apprezzabile solo per pulsazioni molto vicine a quella di
risonanza
Esercizio:
Dato un circuito RLC serie, in cui e’ R=100 Ω, L=0.5 H, C=40µF, si calcolino
la frequenza di risonanza e le frequenze di taglio ω1 e ω2
ω0
1
= 223.6 rad/s ≈ 224 rad/s f 0 =
= 35.6 Hz
ω0 =
2π
LC
ω0 L
Q=
= 1.12
R
1
1
ω 2 = ω0 1 + 2 +
= 345rad / s
4Q
2Q
1
1
ω1 = ω0 1 + 2 −
= 145rad / s
4Q
2Q
ω0
B = ω2 − ω1 = 200rad / s =
= 200rad / s
Q
ω2 ⋅ ω1 = 224 = ω0
CIRCUITO RISONANTE
Esercizio
Determinare la frequenza di risonanza
del circuito di figura
R
1
ωL
+ jωC = 2
+ j ωC − 2
Y=
2 2
2 2
R +ω L
R +ω L
R + jωL
In condizioni di risonanza la parte immaginaria di Y e' nulla
.
R 2C
ω0 L
1
= ω0 C ⇒ ω0 =
1−
2 2
2
L
R + ω0 L
LC