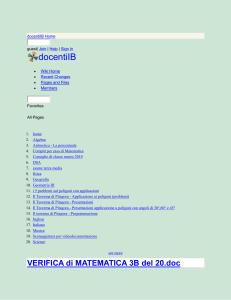
Dimostrazione dell’inverso dell Teorem
Teorema di Pitagora
Teorema di Pitagora
In un triangolo rettangolo (ipotesi). la somma dei quadrati costruiti sui cateti è equivale
equivalente al quadrato
costruito sull’ipotenusa, cioè a²+b² =c² (tesi).
L’inverso del Teorema di Pitagora
Se la somma dei quadrati costruiti
truiti sui cateti è equivalente al quadrato costruito
to sull’ipotenusa,
sull’ip
cioè a²+b²
=c² (ipotesi) allora il triangolo è rettang
rettangolo in ɣ (tesi)
Dimostrazione
Per il teorema del coseno dei triangoli qualsiasi
c² = a²+b² -2ab(cos ɣ)
c.v.d
ma il cos ɣ è = 0 quando ɣ = 90° c.v.d.
Per i triangoli qualsiasi
-
teorema del coseno (T. di Carnot):
C
il quadrato di un lato è uguale
guale alla somma
so
dei quadrati
degli altri due diminuita
iminuita del loro
l
doppio prodotto moltiplicato
o per il cosen
coseno dell’angolo
opposto al primo
o lato (utilizzo:
(utilizz dati due lati e l’angolo fra essi
si compreso); c2=a2+b2–2ab(cos
ɣ)
D
Primo caso ɣ<π/2
Si traccia l’altezza che insiste
ste sul la
lato CA.
BH=a sin ɣ
CH=a cos ɣ
HA=|b-a cos ɣ|
c² =AH²+BH²
c² =(b-a cos ɣ) ²+a² sin ²ɣ
sin ɣ
c² =b ² + a² cos ɣ - 2abcos ɣ+ a² sin²
c²= b² + a² (cos² ɣ+sin² ɣ) -2abcos
2abcos ɣ
c ²=a² + b² -2abcos ɣ
Secondo caso ɣ>π/2
Si traccia l’altezza che insiste
ste sul pr
prolungamento del lato CA.
sin ɣ=sin(π- ɣ)
BH=a sin ɣ
CH=a cos ɣ
HA=b-a cos ɣ
c² =AH²+BH²
c² =(b-a cos ɣ)² +a² sin² ɣ
c² =b² + a ²cos² ɣ - 2abcos ɣ+ a² sin² ɣ
c²= b² + a² (cos² ɣ+sin² ɣ) -2abcos
2abcos ɣ
c ²=a² + b² -2abcos ɣ