Ponte di Wheatstone

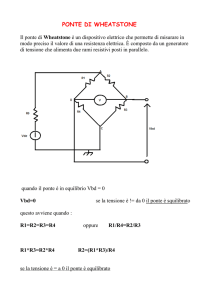
PONTE DI WHEATSTONE
Generalità:
Un metodo classico per la misura di resistenze di ordine medio, è quello del ponte di Wheatstone.
Una schematizzazione di tale ponte è riportata in figura.
Figura- Schema elettrico del Ponte di Wheatstone
Come si può vedere dallo schema elettrico, il ponte di Wheatstone risulta formato da quattro
resistenze connesse in modo dà realizzare i quattro lati di un quadrilatero. Le due diagonali di tale
quadrilatero sono dette diagonale di alimentazione (quella ai cui capi è collegata la tensione
continua di alimentazione V) e diagonale di rilevazione (quella in cui è inserito il galvanometro G
con funzione di rivelatore di zero). In uno dei quattro lati del ponte è inserito il resistore di
resistenza incognita RX, mentre gli altri tre lati contengono resistori campione (la cui resistenza è
quindi nota all’operatore). Il metodo del ponte di Wheatstone richiede che almeno una delle tre
resistenze note sia variabile. In particolare, nello schema riportato in figura il resistore variabile è
indicato con RC. In genere, tale resistore è realizzato con un resistore a decadi.
Il rilevatore di zero G, posto tra i nodi A e B, può essere realizzato sia con un rivelatore di corrente
che con un rivelatore di tensione. È comunque importante che esso sia particolarmente sensibile in
modo da poter rilevare la condizione di azzeramento di corrente o di tensione nella diagonale di
rivelazione. Per adempiere a tale compito esso è inoltre caratterizzato da una scala a zero centrale,
capace, cioè, di apprezzare correnti o tensioni di polarità sia positiva che negativa. Quando il
rivelatore di zero indica la condizione di azzeramento nella diagonale di rivelazione (condizione
individuata dall'indice del galvanometro nella posizione centrale di zero), si dice che il ponte ha
raggiunto la condizione di equilibrio.
Il generatore di tensione continua E alimenta il ponte attraverso il potenziometro R e fa scorrere, da
C verso D, una corrente che si ripartisce tra i due rami comprendenti rispettivamente il nodo A e il
nodo B. Applicando le relazioni del partitore di tensione ai due rami del ponte, si possono calcolare
i potenziali dei nodi A e B rispetto al nodo D (preso come potenziale di riferimento) e quindi la
differenza di potenziale VAB:
V A= V ⋅
RB
R A + RB
V B= V ⋅
RC
R X + RC
 RB
RC 

−
V AB = V A − VB = V ⋅ 
+
+
R
R
R
R
B
X
C 
 A
Imponendo la condizione VAB=0, si ricava la relazione che lega le quattro resistenze del ponte,
quando è verificata la condizione di equilibrio:
RC
RB
V AB = 0 ⇒
=
⇒ RB R X + RB RC = R A RC + RB RC ⇒ RB R X = R A RC
R A + RB R X + RC
In questa condizione il prodotto delle resistenze dei due lati opposti eguaglia il prodotto delle altre
due. È quindi possibile dedurre la resistenza incognita RX:
R
R X = A RC
RB
Di conseguenza, per ricavare il valore della resistenza incognita RX, si può agire o sul valore del
rapporto RA/RB o sul valore della resistenza RC. Nel seguito si farà riferimento alla soluzione con
RA/RB costante ed RC variabile.
Procedura di misura
Nella fase iniziale della misura, il valore di RC potrebbe essere molto diverso da quello che soddisfa
la condizione di equilibrio, per cui la corrente nel ramo AB potrebbe essere di valore troppo elevato
rispetto al fondo scala del rivelatore di zero. Di conseguenza, si preferisce alimentare il circuito del
ponte di Wheatstone con tensioni variabili, usando tensioni molto basse in fase iniziale, quando cioè
si rischia di essere lontani dalla condizione di equilibrio del ponte. Agendo sul resistore a decadi RC,
si porta il ponte in condizioni prossime a quelle di equilibrio, procedendo, poi ad aumentare la
tensione di alimentazione. Si procede poi, per approssimazioni successive, operando
alternativamente con azzeramenti del ponte ed aumenti della tensione di alimentazione. Operando
con tale procedura, si ha il vantaggio di raggiungere elevate sensibilità del ponte senza correre il
rischio di danneggiare il rivelatore di zero (il quale opera sempre con correnti o tensioni prossime a
zero, inizialmente a causa di una bassa tensione di alimentazione, successivamente per il
raggiungimento della condizione di equilibrio). L’azzeramento del ponte si effettua operando sul
resistore a decadi RC, mentre il circuito potenziometrico (realizzato con il reostato R) viene usato
per incrementare la tensione di alimentazione man mano che si procede nel raggiungimento della
condizione di equilibrio. In tale procedura, all’aumentare della tensione di alimentazione, si opera
sulle decadi via via meno significative della resistenza campione RC.
Al crescere della sensibilità del ponte, può risultare impossibile raggiungere l’azzeramento del
rivelatore di zero in quanto la resistenza campione a decadi, per sua natura, fornisce variazioni
discrete di resistenza (in genere con risoluzione massima del decimo di ohm). Il valore di equilibrio
può essere, in tal caso, desunto adoperando una tecnica di interpolazione lineare. Si supponga, ad
esempio, di aver cablato un ponte di Wheatstone in cui risulti RA=RB=1000 Ω e di voler misurare
una resistenza RX=8715,73 Ω operando con un resistore campione con decade meno significativa di
0.1 Ω/step. In tale ipotesi, non si riesce a portare a zero l'indice del galvanometro né impostando
RC=8715,7 Ω , né con RC =8715,8 Ω. Si può ,allora, effettuare l'interpolazione del valore di RX col
seguente procedimento. Se con RC=8715,7 Ω l'indice del rivelatore di zero devia da un lato (per
esempio a sinistra dello zero), di 5 divisione e con RC=8715,8 Ω devia, invece, dall'altro lato di 10
divisioni, si può ricavare il valore di ∆RX da aggiungere a 8715,7 Ω onde avere il valore della RX.
Ipotizzando la linearità del rivelatore di zero nell’intorno dello zero, si esegue l’interpolazione
lineare per calcolare ∆RX e quindi ricavare RX.
(8715,8 − 8715,7 ) : (5 − (− 10)) = ∆R X : 5
0,1 : 15 = ∆R X : 5
0,1 ⋅ 5 0,1
=
= 0,0 3 Ω
15
3
R X = (8715,7 + 0,0 3 ) = 8715,7 3 Ω
In figura si riporta, per maggiore chiarezza, una interpretazione grafica del procedimento sopra
descritto. A tal fine, si riportano, in senso opposto rispetto al segmento AC=0,1 Ω (eguale cioè alla
differenza tra 8715,8 e 8715,7 ), le due deviazioni AB = 5 e CD = 10 (cioè due segmenti ad esse
proporzionali), si congiungono gli estremi B e D di tali segmenti e l’intercetta individua il punto O
sul segmento AC che rappresenta appunto il valore interpolato (8715,73 Ω):
∆R X =
C
B
5
10
D 8715,8Ω
O
8715,73 Ω
A
8715,7 Ω
5
0
10
Interpolazione lineare
Valutazione incertezza
L'incertezza sulla misura di RX può essere valutata applicando la legge di propagazione
dell'incertezza suggerita dalle Norma UNICEI 9 alla formula che esprime la condizione di
equilibrio. In realtà, la sensibilità del galvanometro non è infinita, (e ciò comporta che esso indica
una corrente nulla anche quando la corrente è inferiore ad un certo valore minimo). Di conseguenza
nella relazione di equilibrio bisogna tener conto che non si è sensibili a variazioni di resistenza che
determinano il passaggio di una corrente inferiore a quella minima determinata dalla sensibilità del
metodo. Di questo se ne può tendere conto riscrivendo la relazione di equilibrio nel seguente modo:
R
R X = A RC + RS
RB
in cui RS rappresenta appunto la variazione di resistenza RX che darebbe luogo ad uno spostamento
dell'ago del galvanometro della minima quantità apprezzabile. Per la valutazione di RS si può
procedere in due modi distinti: approccio sperimentale o approccio teorico. In entrambi i casi
bisogna valutare il minimo scostamento RS di RX a cui il ponte è sensibile.
Approccio sperimentale per la valutazione dell'incertezza di sensibilita'
Ipotizzando un comportamento lineare intorno allo zero del galvanometro è possibile scrivere:
∆R X
∆R X : ∆λ = RS : dλ ⇒ RS =
⋅ dλ
∆λ
in cui:
∆RX è la variazione ipotetica di resistenza RX a cui corrisponde uno spostamento dell’indice del
rivelatore di zero di ∆λ deviazioni, RS l’incertezza di sensibilità, dλ il minimo spostamento
apprezzabile dell’indice del galvanometro (per esempio di 0,5 deviazioni).
Ne consegue che RS si potrebbe valutare dando variazione significative a RX e, ipotizzando la
linearità del galvanometro nell’intorno dello zero, individuando la variazione che sarebbe
necessario imprimere ad RX per ottenere la minima variazione appressabile sul galvanometro. Nella
frase precedente è stato usato il condizionale in quanto non si può fisicamente dare una variazione
alla resistenza incognita RX che è stata supposta fissa. Però, osservando la relazione di equilibrio del
ponte e differenziandone ambo i membri si ottiene:
R
R X = A ⋅ RC
RB
R
 R
∆R X = ∆ A ⋅ RC  = A ⋅ ∆RC
 RB
 RB
∆RC
∆R X R A ∆RC R A ∆RC
=
⋅
=
⋅
=
RC
RX
RB R X
RB R A
⋅ RC
RB
Quindi, la RS si può valutare dando una variazione significativa alla resistenza campione RC
(resistenza variabile) anziché ad RX. Ne consegue che si può scrivere:
∆RC
RS =
⋅ dλ
∆λ
Proviamo a valutare l’incertezza di sensibilità per via sperimentale con riferimento all'esempio
numerico precedentemente riportato. Impostando RC=8715,7Ω erano state riscontrate 5 deviazioni a
sinistra dello 0, mentre impostando RC=8715,8Ω erano state riscontrate 10 deviazioni a destra dello
0. Inoltre si è ipotizzato che l'operatore riesce ad apprezzare ½ divisione. Risulta che
∆RC=(8715,8−8715,7)=0,1Ω, ∆λ=(5-(-10))=15 deviazioni, dλ=0,5 (mezza deviazione).
Sostituendo tali valori nella formula precedente si ricava:
∆RC
0,1
RS =
⋅ dλ =
⋅ 0,5 = 0,00 3Ω
15
∆λ
Approccio teorico
Scomponendo il circuito del ponte di Wheatstone nel circuito equivalente di Thevenin tra i punti A
e B. Ipotizzando nulla la resistenza interna dell'alimentatore si ha:
R ⋅R
R ⋅R
REQ = A B + X C
R A + RB R X + RC
La tensione a vuoto risulta:
 RX
RA 

E0 = E ⋅ 
−
R
R
R
R
+
+
C
A
B 
 X
Individuato il circuito equivalente secondo Thevenin, per risalire al valore di RS si ricordi che essa è
definita come la variazione di resistenza dalle condizioni di equilibrio alla quale corrisponde un
passaggio di corrente nel galvanometro pari alla minima corrente alla quale il galvanometro è
sensibile (IMIN):
∆E0
I MIN =
REQ + RI
in cui ∆E0 è la variazione di tensione rispetto alla condizione di equilibrio dovuta alla variazione di
RS. Per ricavare ∆E0 si può ipotizzare di trovarsi in condizioni di linearità. Tale approssimazione è
valida poiché la variazione RS è sufficientemente piccola.
L’ipotesi di linearità implica che ∆E0 = k RS in cui il coefficiente k esprime un coefficiente di
sensibilità che, come al solito, può essere posto sotto forma di derivata parziale:
∂E
k= 0
∂R X
Dalle precedenti relazioni risulta che ∆E0 è esprimibile come:
∂E0
∆E0 = I MIN ⋅ (REQ + RI ) =
⋅ RS
∂R X
da cui risulta:
I MIN ⋅ (REQ + RI )
RS =
∂E0
∂R X
La corrente IMIN si può esprimere, in base alla costante strumentale specifiche del galvanometro KG.
La costante strumentale di un galvanometro può essere espressa in due modi: o come
ampere/divisione oppure come divisioni/ampere. Esprimendo tale costante come ampere/divisione,
la corrente che circola nel galvanometro si ottiene moltiplicando la deflessione dell’indice (espressa
in numero di divisioni) per tale costante:
I MIN = K G ⋅ dλ
Questa costante è concettualmente l'inverso della sensibilità, intesa come qualità dello strumento,
nel senso che quanto più piccola è KG tanto migliore è la sensibilità dello strumento. Sostituendo
IMIN nell’espressione di RS si ottiene:
K G ⋅ dλ ⋅ (REQ + RI )
RS =
∂E0
∂R X
∂E 0
Infine per calcolare RS bisogna ancora valutare il termine
derivando l’espressione di E0
∂R X
rispetto ad RX.
 RX
RA 
 ⇒
E0 = E ⋅ 
−
R
R
R
R
+
+
C
A
B 
 X
R + RC − R X
RC
∂E0
=E
=E
=E X
2
∂R X
(RX + RC )
(R X + RC )2
RC
 R 
R X2 ⋅ 1 + C 
 Rx 
2
=
RC
RX
E
R X  RC  2

1 +
 Rx 
da cui infine si ricava:
RS =
K G ⋅ dλ ⋅ (REQ + RI )
RC
RX
E
R X  RC  2

1 +
 Rx 
Tecnica della doppia pesata
Risulta conveniente utilizzare due resistori RA ed RB caratterizzati dagli stessi valori nominali. A
causa della loro incertezza i due valori effettivi di RA ed RB saranno differenti. Effettuando due
misure e scambiando di posto RA ed RB si ha:
RX =
RA
RC1
RB
RB
RC 2
RA
in cui RC1 ed RC2 rappresentano i valori della resistenza a decadi in corrispondenza dei due
equilibri. Moltiplicando membro a membro si ha:
R X2 = RC1 ⋅ RC 2 ⇒ R X = RC1 ⋅ RC 2
RX =