PONTE DI WHEATSTONE

PONTE DI WHEATSTONE
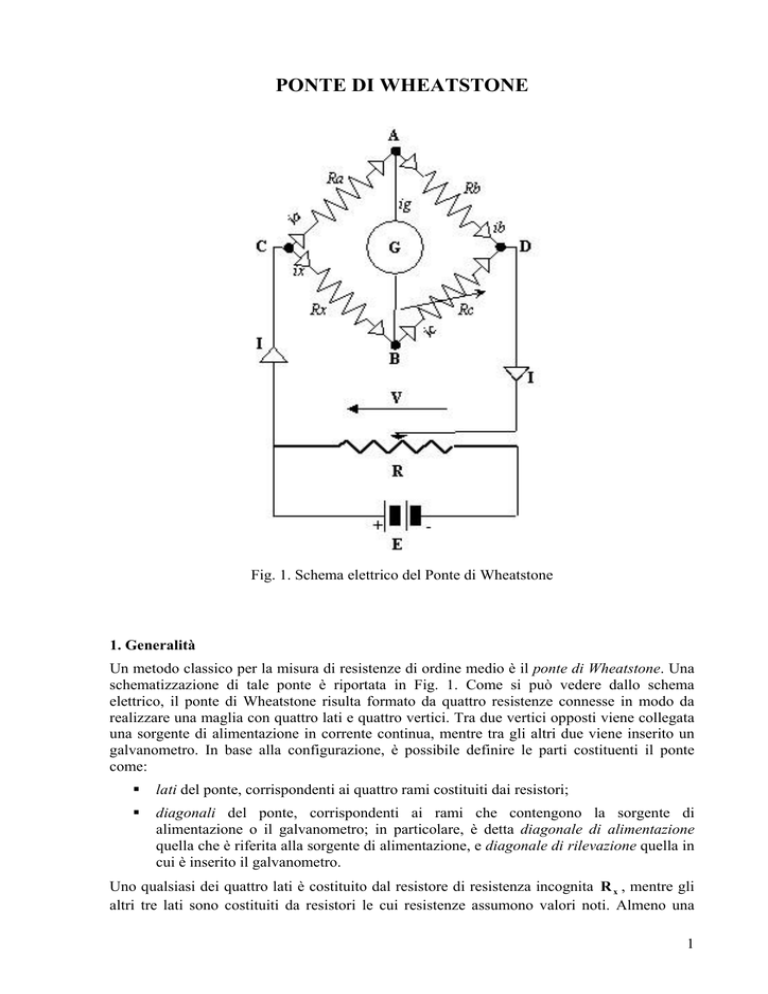
Fig. 1. Schema elettrico del Ponte di Wheatstone
1. Generalità
Un metodo classico per la misura di resistenze di ordine medio è il ponte di Wheatstone. Una
schematizzazione di tale ponte è riportata in Fig. 1. Come si può vedere dallo schema
elettrico, il ponte di Wheatstone risulta formato da quattro resistenze connesse in modo da
realizzare una maglia con quattro lati e quattro vertici. Tra due vertici opposti viene collegata
una sorgente di alimentazione in corrente continua, mentre tra gli altri due viene inserito un
galvanometro. In base alla configurazione, è possibile definire le parti costituenti il ponte
come:
ƒ
lati del ponte, corrispondenti ai quattro rami costituiti dai resistori;
ƒ
diagonali del ponte, corrispondenti ai rami che contengono la sorgente di
alimentazione o il galvanometro; in particolare, è detta diagonale di alimentazione
quella che è riferita alla sorgente di alimentazione, e diagonale di rilevazione quella in
cui è inserito il galvanometro.
Uno qualsiasi dei quattro lati è costituito dal resistore di resistenza incognita R x , mentre gli
altri tre lati sono costituiti da resistori le cui resistenze assumono valori noti. Almeno una
1
delle resistenze note deve essere anche variabile, ed in particolare nell’esempio di sopra
riportato avrò un resistore variabile R c a decadi. Il rilevatore di zero, posto tra i nodi A e B, è
sensibile al passaggio di corrente nel lato stesso, o alla differenza di potenziale tra i nodi A e
B.
Il ponte è in equilibrio quando è nulla la corrente che attraversa la diagonale di rivelazione,
condizione che può essere individuata dall’indice del galvanometro nella posizione di zero. In
condizione di funzionamento, il generatore di tensione continua E fa scorrere una corrente che
si ripartisce tra i due rami in cui sono inserite R a ed R x comprendenti rispettivamente il nodo
A e il nodo B. Applicando i principi di Kirchhoff al ponte, quando è verificata la condizione
di equilibrio, si ha:
equazione al nodo A
Ia = Ib
(1)
equazione al nodo B
Ix = Ic
(2)
equazione alla maglia ABC
R x ⋅ I x = Ra ⋅ Ia
(3)
equazione alla maglia ABD
R c ⋅ Ic = Rb ⋅ Ib
(4)
Sostituendo (1) e (2) in (4), si ottiene:
R x ⋅ I x = Ra ⋅ Ia
(5)
Rc ⋅ I x = Rb ⋅ Ia
(6)
Dividendo membro a membro, si ricava:
Rx Ra
=
Rc Rb
da cui:
Rb ⋅ R x = Ra ⋅ Rc
(7)
E’ stata cosi trovata la relazione che lega le quattro resistenze del ponte, in condizioni di
equilibrio: il prodotto delle resistenze dei due lati opposti eguaglia il prodotto delle altre due.
E’ quindi possibile calcolare il valore della resistenza incognita:
Rx =
Ra
⋅ Rc
Rb
(8)
Ra
(ponti a filo)
Rb
o sulla resistenza R c . Nel seguito si farà riferimento a questa seconda soluzione.
Per raggiungere la condizione di equilibrio è possibile operare sul rapporto
2
2. Procedura di misura
Poiché inizialmente il valore di R c potrebbe anche essere molto diversa da quello che
soddisfa la (8), la corrente nel ramo AB potrebbe essere elevata e quindi danneggiare il
galvanometro. Di conseguenza si preferisce alimentare il circuito con valori di tensione via
via crescenti fino al valore nominale, incrementando contemporaneamente la sensibilità del
galvanometro. Normalmente all’aumentare della tensione di alimentazione e della sensibilità
del galvanometro, occorre operare sulle decadi più piccole dalla resistenza campione R c .
Anche con una sensibilità del ponte elevata ed in condizioni di tensione di alimentazione
nominale, a causa del numero finito di decadi della resistenza R c a disposizione, può
accadere di non riuscire ad ottenere un perfetto azzeramento del galvanometro: in tal caso, è
necessario procedere alla interpolazione lineare, procedimento valido in quanto sia il
circuito sia lo strumento (galvanometro) hanno comportamento lineare nell’intorno dello zero.
Per esempio, ponendo R a = R b =1000 Ω, ipotizzando R x = 8715,4 Ω ed avendo a disposizione
una R c con decade più piccola pari ad 1 Ω, non si riuscirà a portare a zero l’indice del
galvanometro né con R c = 8715 Ω né con R c = 8716 Ω. E’ necessario quindi effettuare
l’interpolazione del valore di R x col seguente procedimento. Supponendo che con
R c = 8715 Ω l’indice devia da un lato (per esempio a sinistra dello zero), di δ 1 divisioni e
con R c = 8716 Ω devia, invece, dall’altro lato di δ 2 divisioni, e detto x il valore di resistenza
da sommare al valore più piccolo di R c per ottenere l’azzeramento del galvanometro, è
possibile costruire la seguente figura:
Fig. 2. Rappresentazione grafica dell’interpolazione
dove il segmento AC rappresenta la differenza fra i due valori di R c (ovvero 1 Ω) ed i
segmenti AB e CD rappresentano rispettivamente le due deviazioni δ 1 e δ 2 , riportate in
senso opposto rispetto al segmento AC. Congiungendo gli estremi B e D, si ottengono due
triangoli rettangoli ABO e OCD che risultano essere simili (essendo AB parallelo a CD ed
3
entrambi perpendicolari ad AC, e gli angoli BOA e COD eguali perché opposti al vertice). Si
AO δ1
ha, quindi:
= , e dato che AO = x ed OC = (1-x), sarà ancora :
OC δ 2
δ
x
= 1
1 − x δ2
da cui:
x=
δ1
δ1 + δ 2
Se ad esempio è δ 1 = 14 divisioni e δ 2 = 21 divisioni, sarà
x=
14
14
=
= 0,4 Ω
21 + 14 35
e quindi
R c = 8715,4 Ω
che è il valore di R c da considerare nella (8).
4
3. Valutazione dell’incertezza
L’incertezza sulla misura di R x può essere valutata applicando la legge di propagazione
dell’incertezza suggerita dalle Norma UNICEI 9 alla relazione (8).
Bisogna però tenere presente che la sensibilità del galvanometro non è infinita, e che quindi
può dare una indicazione di zero anche quando in realtà circola una corrente non nulla. Detta
I min la corrente limite al di sotto della quale il galvanometro è insensibile (ovvero fornisce
comunque una indicazione di zero), la relazione (8) va riscritta per tener conto che il ponte
non è sensibile a variazioni della resistenza R x che determinano il passaggio di una corrente
inferiore a I min :
Rx =
Ra
⋅ Rc + R s
Rb
dove R s è il valore di resistenza corrispondente alla corrente limite I min . Considerando la
natura della resistenza R s (che può esserci o meno, e può assumere qualsiasi valore fino ad
un valore massimo pari proprio ad R s ), essa può essere considerata come una grandezza
aleatoria a valore medio nullo ma con una incertezza u Rs diversa da zero, da valutare. Di
conseguenza:
u 2Rx = u ⎛2 Ra ⋅ Rb ⎞ + u 2Rs
⎜⎜
⎝
Rc
⎟⎟
⎠
L’incertezza u ⎛ Ra ⋅ Rb ⎞ si ottiene applicando la legge di propagazione delle incertezze nel caso
⎜⎜
⎝
Rc
⎟⎟
⎠
di un prodotto o di un rapporto:
u& ⎛2 Ra ⋅ Rb ⎞ = u& 2Ra + u& 2Rb + u& 2Rc
⎜⎜
⎝
⎟⎟
⎠
Rc
2
u
2
⎛ R a ⋅ Rb
⎜⎜
⎝ Rc
⎞
⎟⎟
⎠
⎛ R ⋅R ⎞
= ⎜⎜ a b ⎟⎟ ⋅ u& ⎛2 Ra ⋅ Rb ⎞ = R 2x ⋅ u& 2Ra + u& 2Rb + u& 2Rc .
⎟⎟
⎜⎜
⎝ Rc ⎠
⎝ Rc ⎠
(
)
L’incertezza sulle singole resistenze R a , R b , R c può essere rilevata con metodi di valutazione
di categoria A, cioè eseguendo misure ripetute, o di tipo B, utilizzando i dati forniti dal
costruttore.
Per valutare u Rs bisogna ragionare come segue. Per come è stata definita, la resistenza R s
rappresenta il valore limite di variazione della resistenza incognita che dà luogo ad uno
spostamento dell’ago del galvanometro della minima quantità apprezzabile. Per la valutazione
di R s si può procedere in due modi distinti: approccio a posteriori (sperimentale) o approccio
a priori (teorico). Una volta determinata la R s , è possibile adottare un metodo di valutazione
dell’incertezza di tipo B, ipotizzando una distribuzione rettangolare a media nulla e di
ampiezza ± R s 2 ; si ha quindi:
u Rs =
Rs
R
= s .
2 3
12
Nel seguito vengono presentati entrambi gli approcci per la valutazione di R s .
5
3.1. Approccio a posteriori
Ipotizzando un comportamento lineare del galvanometro intorno allo zero, è possibile
scrivere:
dR x : dλ = ΔR x : Δλ
Ovvero:
R s : dλ = ΔR x : Δλ
(9)
dove si è indicato con:
ƒ R s = il valore della minima variazione dR x della R x a cui il ponte è sensibile;
ƒ dλ = minima deviazione apprezzabile dello strumento;
ƒ ΔR x = variazione finita di R x ;
ƒ Δλ= il numero di deviazioni corrispondenti alla variazione finita ΔR x .
Dalla relazione (9) si ha:
Rs =
ΔR x
⋅ dλ
Δλ
(10)
per cui è possibile valutare R s imponendo una variazione significativa a R x . Tuttavia, nelle
usuali applicazioni, tale variazione non si può fisicamente imporre in quanto R x è la
resistenza incognita e normalmente non è variabile. Dalla relazione(8), si ha:
⎛R
⎞ R
ΔR x = Δ⎜⎜ a ⋅ R c ⎟⎟ = a ⋅ ΔR c
⎝ Rb
⎠ Rb
in quanto l’unica resistenza variabile è la R c . Dividendo per R x e ricordando sempre la (8),
si ha:
ΔR x R a ΔR c R a ΔR c
ΔR c
=
⋅
=
⋅
=
R
Rx
Rb R x
Rb
Rc
a
⋅ Rc
Rb
di conseguenza, essendo R x ≅ R c , la (10) diviene:
R s = ΔR c ⋅
dλ R x
dλ
⋅
≅ ΔR c ⋅
Δλ R c
Δλ
Quindi la R s si può valutare imponendo una variazione significativa alla resistenza campione
R c e valutando la corrispondente deviazione Δλ del galvanometro. Con riferimento
all’esempio numerico precedentemente riportato ( R x = 8715,4 Ω; R a = R b ; R′c = 8715 Ω e
R′c′ =8716 Ω, e quindi per una variazione ΔR c =1 Ω) con le rispettive deviazioni ( δ 1 = 14
divisioni a sinistra e δ 2 = 21 a destra, per un totale di Δλ = 35 divisioni), e considerando di
poter apprezzare sul galvanometro la mezza divisione (dλ = 0,5), si ha:
R s = ΔR c ⋅
dλ
0,5
= 1⋅
= 0.014 Ω
35
Δλ
6
3.2. Approccio a priori
L’approccio a priori si basa sul teorema di Thevenin, ovvero sull’analisi del circuito
equivalente del ponte visto ai capi del galvanometro:
Fig. 3. Circuito equivalente di Thevenin
Per definire i valori di R eq e di E0 si procede come segue.
Con riferimento allo schema elettrico del ponte di Fig. 4, si consideri il circuito equivalente
visto dai vertici di rilevazione A e B ottenuto cortocircuitando il generatore (Fig. 5):
Fig. 4. Schema elettrico del ponte
Fig. 5. Circuito equivalente visto ai capi del galvanometro
da cui:
R eq =
Ra ⋅ Rb
R ⋅R
+ x c
R a + Rb R x + Rc
Con riferimento sempre allo schema di Fig. 4, è possibile ricavare:
7
VA = E ⋅
Ra
Ra + Rb
VB = E ⋅
;
Rx
R x + Rc
⎛ Rx
Ra ⎞
⎟⎟
E o = VB − VA = E ⋅ ⎜⎜
−
⎝ R x + Rc Ra + Rb ⎠
(11)
In condizione di equilibrio I g = 0 e quindi VAB = E0 = 0. Per risalire al valore di R s si
ricordi che essa è definita come la variazione di resistenza R x alla quale corrisponde un
passaggio di corrente I g nel galvanometro pari alla minima corrente alla quale il
galvanometro è sensibile.
Analizzando il circuito di Fig. 3 si ha:
Ig =
ΔE0
R eq + R g
(12)
dove ΔE o è la variazione di tensione dovuta alla R s ed R g è la resistenza interna del
galvanometro. Per ricavare ΔE 0 si può sviluppare la relazione (11) in serie di Taylor
nell’intorno di R x a cui corrisponde E 0 = 0 , arrestandosi al primo ordine (tale
approssimazione è valida poiché la variazione di R x sono piccole); si ha:
ΔE0 =
∂E0
∂E0
⋅ dR x =
⋅ Rs
∂R x
∂R x
(13)
Dalle (12) e (13) si ha:
ΔE0 = (R eq + R g ) ⋅ I g =
cioè
Rs =
(R
eq
∂E0
⋅ Rs
∂R x
+ R g )⋅ I g
∂E0
∂R x
(14)
La corrente I g si può esprimere come:
I g = K g ⋅ Δλ
(15)
dove K g è la costante strumentale del galvanometro, espressa in A/div. Questa costante è
legata in maniera inversa alla sensibilità dello strumento, in quanto tanto più piccola è K g
tanto migliore è la sensibilità dello strumento.
Dalla (11) si ha:
R + Rc − R x
Rc
∂E0
= E⋅
= E⋅ x
=E⋅
2
∂R x
(R x + R c )
(R x + R c )2
Rc
⎛ R ⎞
R 2x ⋅ ⎜⎜1 + c ⎟⎟
⎝ Rx ⎠
2
=
Rc
Rx
E
⋅
R x ⎛ R ⎞2
⎜⎜1 + c ⎟⎟
⎝ Rx ⎠
(16)
per cui la (14) diventa:
8
2
(R eq + R g )⋅ ⎛⎜⎜1 + RR c ⎞⎟⎟ 2
R
x ⎠
⎝
Rs =
⋅ x ⋅ K g ⋅ Δλ
E
Rc
∂E0
compare al denominatore, è interessante andare a
∂R x
valutare, onde dimensionare al meglio il circuito, quando esso assume il valore massimo per
poter così ottenere il minimo valore di R s e quindi la condizione di massima sensibilità.
Poiché nella relazione (14) il termine
Ponendo
Rc
= m nella (16), si ha:
Rx
E
∂E0
m
=
⋅
∂R x R x (1 + m )2
∂E0
∂R x
Per individuare il massimo in funzione di m si deve porre
= 0 , cioè:
∂m
(1 + m)2 − 2 ⋅ (1 + m ) ⋅ m = 1 + 2m + m2 − 2m − 2m2
(1 + m)4
(1 + m)4
=
− m2 + 1
=0
(1 + m)4
che è verificata per m = ±1, ovvero la condizione di massima sensibilità del ponte è ottenuta
per R x = R c ; in tal caso, ovviamente, anche R a = R b . E’ possibile inoltre dimostrare che la
migliore condizione in assoluto è quella per la quale R x = R c = R a = R b .
Considerando solo la soluzione positiva (
Rc
= 1 ) e sostituendo tale valore nella (16), si ha:
Rx
E 1
E
∂E0
=
⋅ 2 =
∂R x R x (2)
4R x
per cui la (14) diventa:
Rs =
(R
eq
+ R g ) ⋅ 4R x
⋅ K g ⋅ Δλ
E
Si può, quindi, affermare che:
ƒ
uno strumento con un K g più piccolo riduce l’errore di sensibilità;
ƒ
quanto più è elevata la tensione E tanto più basso è l’errore di sensibilità; tuttavia, il
valore massimo di E dipende dalla corrente massima ammissibile per i componenti;
ƒ
quanto più piccolo è il termine (R eq + R g ) tanto più bassa è R s ; quindi l’errore di
sensibilità non dipende solo dallo strumento utilizzato, ma anche dalle caratteristiche
del circuito;
ƒ
il metodo presenta un limite al crescere di R x , in quanto aumenta la R s sia per
dipendenza diretta sia perché aumenta la R eq , e di conseguenza diminuisce la
sensibilità.
9
4. Miglioramento della precisione del metodo del ponte di Wheatstone
Il ponte di Wheatstone viene utilizzato per misure di resistenza di valore medio, assicurando
precisioni dell’ordine di una parte su diecimila. Sembrerebbe quindi che, trattandosi di
precisioni non particolarmente elevate, esso possa essere sostituita da un buon multimetro
numerico.
In realtà attraverso le due tecniche:
ƒ
doppia pesata
ƒ
sostituzione
si ha un miglioramento delle prestazioni tale da giustificare l’utilizzo del ponte anche per
misure di precisione.
4.1. Tecnica della doppia pesata
Come detto risulta sempre conveniente utilizzare due resistori R a ed R b caratterizzate dagli
stessi valori nominali. Effettuando due misure su R x e scambiando di posto R a ed R b si ha:
Rx =
Ra
⋅ R c1
Rb
(17)
Rx =
Rb
⋅ R c2
Ra
(18)
A causa della incertezza su R a e R b , pur avendo nominalmente R a = R b si avrà R c1 ≠ R c2 .
Moltiplicando i due membri delle relazioni (17) e (18) si ha:
R 2x =
Ra
R
⋅ R c1 ⋅ b ⋅ R c 2 = R c1 ⋅ R c 2
Rb
Ra
(19)
da cui:
(20)
R x = R c1 ⋅ R c 2
con R c1 ≅ R c2 in quanto la differenza fra i due valori è dovuta solamente all’incertezza su R a
e R b . Utilizzando per R c una resistenza a decadi, è possibile considerare:
R c1 = R 0 + r1
(21)
R c 2 = R 0 + r2
in cui R 0 è la parte comune della R c nelle due misure ed ovviamente R 0 >> r1 ed R 0 >> r2 .
La (20) diviene quindi:
Rx =
(R 0 + r1 ) ⋅ (R 0 + r2 ) =
R 02 + R 0 ⋅ (r1 + r2 ) + r1 ⋅ r2
r + r r ⋅r
r +r
= R0 ⋅ 1 + 1 2 + 1 22 ≅ R0 ⋅ 1 + 1 2
R0
R0
R0
(22)
10
in quanto il termine
r1 ⋅ r2
n
risulta trascurabile. Ricordando inoltre che (1 + α ) con α << 1
2
R0
può essere approssimato come (1 + α ) ≅ 1 + nα , ed essendo sempre r1 ed r2 << R 0 per cui
r1 + r2
<< 1 , la (22) diviene
R0
n
⎛ r + r ⎞ ⎛ 2R 0 + r1 + r2 ⎞ R c1 + R c 2
R x = R 0 ⋅ ⎜⎜1 + 1 2 ⎟⎟ = ⎜
⎟=
2R 0 ⎠ ⎝
2
2
⎠
⎝
e cioè il valore di R x si ottiene come media delle due misure.
Valutazione dell’incertezza
Per valutare l’incertezza bisogna tener conto anche dell’incertezza legata alla sensibilità del
ponte. A tal fine le equazioni (17) e (18), conformemente a quanto visto in precedenza, vanno
così riscritte:
Rx =
Ra
⋅ R c1 + R s1
Rb
Rx =
Rb
⋅ R c2 + R s 2
Ra
quindi, moltiplicando membro a membro:
⎛R
⎞
⎛R
⎞
R x = R c1 ⋅ R c2 + R s1 ⋅ ⎜⎜ b ⋅ R c2 ⎟⎟ + R s2 ⋅ ⎜⎜ a ⋅ R c1 ⎟⎟ + R s1 ⋅ R s2 ≅
⎝ Ra
⎠
⎝ Rb
⎠
(
)
dato che R s1 ⋅ R s 2 ≅ 0 e ponendo come prima R c1 = R 0 + r1 e R c 2 = R 0 + r2 , si ha:
≅ R 02 + R 0 ⋅ (r1 + r2 ) + r1 ⋅ r2 +
= R0 ⋅ 1 +
R s1 ⋅ R b
Ra
r1 + r2 r1 ⋅ r2 R s1 ⋅ R b
+ 2 +
R0
R0
Ra
⋅ (R 0 + r2 ) +
R s2 ⋅ R a
Rb
⎛ 1
r ⎞ Rs ⋅ Ra
⋅ ⎜⎜
+ 22 ⎟⎟ + 2
Rb
⎝ R0 R0 ⎠
⎛ 1
r ⎞
⋅ ⎜⎜
+ 12 ⎟⎟ ≅
⎝ R0 R0 ⎠
⎛r
1 ⎞ ⎛ r1
1 ⎞
⎟⎟ e ⎜⎜ 2 <<
⎟ e potendo trascurare il termine
essendo ⎜⎜ 22 <<
R0 ⎠ ⎝ R0
R 0 ⎟⎠
⎝ R0
≅ R0 ⋅ 1 +
r1 + r2
1
+
R0
R0
il
termine
⎡ r +r
1
≅ R 0 ⋅ ⎢1 + 1 2 +
2R 0 2R 0
⎣
⎛ r1 ⋅ r2 ⎞
⎜⎜ 2 ⎟⎟ , si ha:
⎝ R0 ⎠
⎛ R s ⋅ R b R s2 ⋅ R a ⎞
⎟⎟ ≅
⋅ ⎜⎜ 1
+
R
R
a
b
⎝
⎠
⎡ r1 + r2 1 ⎛ R s1 ⋅ R b R s2 ⋅ R a ⎞⎤
⎟⎥ << 1 ,
+
⋅⎜
+
⎢
R 0 ⎜⎝ R a
R b ⎟⎠⎦
⎣ R0
n
l’approssimazione (1 + α ) ≅ 1 + nα , per cui:
essendo
⋅ (R 0 + r1 ) =
è
possibile
applicare
⎛ R s ⋅ R b R s2 ⋅ R a ⎞ ⎤
⎟⎥ =
⋅ ⎜⎜ 1
+
R b ⎟⎠⎦
⎝ Ra
11
= R0 +
r1 + r2 1 ⎛
R
R ⎞
+ ⋅ ⎜⎜ R s1 ⋅ b + R s2 ⋅ a ⎟⎟ ≅
2
2 ⎝
Ra
Rb ⎠
essendo R a = R b :
≅ R0 +
r1 + r2 R s1 + R s 2
+
2
2
e quindi:
1
1
1
1
u R2 X = u R2 0 + u r21 + ur22 + u 2R S1 + u 2R S2
4
4
4
4
4.2. Tecnica della sostituzione
Tale metodo consente di ottenere un incertezza ridotta nella misura del rapporto tra due
resistenze che differiscono fra loro di una quantità piccola. Questa situazione è anche quella
che si ha nelle applicazioni con resistenze incognite variabili in cui si è interessati a misurare
la variazione relativa della resistenza incognita rispetto ad una condizione di riferimento.
Si procede nel seguente modo. Si pone una delle due resistenze incognite R x1 nel ponte e si
raggiunge l’equilibrio:
R x1 =
Ra
⋅ R c1
Rb
Quindi si sostituisce la R x1 con l’altra resistenza incognita R x 2 e si ricava una nuova
condizione di equilibrio:
Rx2 =
Ra
⋅ Rc2
Rb
Quindi dividendo membro a membro:
α=
R x1
Rx2
=
R c1
Rc2
Per valutare l’incertezza sul rapporto bisogna tener conto dell’incertezza sulle due condizioni
di equilibrio; si ha:
α=
R c1 + R s1
Rc2 + Rs2
(23)
Dato che R c1 e R c 2 sono due valori diversi dello stesso resistore a decadi, è possibile porre:
R c1 = R 0 + r1
R c 2 = R 0 + r2
dove r1 e r2 sono piccole rispetto a R x1 e R x 2 e sono molto prossime tra loro.
L’espressione (23) diventa quindi:
12
α=
R 0 + r1 + R s1
R 0 + r2 + R s 2
r1 + R s1
1+
R0
r2 + R s 2
=
1+
R0
se R 0 >> r2 + R s 2 , applicando l’approssimazione (1 + α ) ≅ 1 + nα , l’espressione diventa:
n
⎛ r + R s1
α ≅ ⎜⎜1 + 1
R0
⎝
⎞ ⎛ r2 + R s 2
⎟⎟ ⋅ ⎜⎜1 −
R0
⎠ ⎝
(
) (
) (
(r − r ) + R s1 − R s 2 r1 + R s1 ⋅ r2 + R s 2
⎞
⎟⎟ = 1 + 1 2
−
R0
R 02
⎠
2
)
2
poiché r1 e r2 così come R s1 e R s 2 sono molto minori di R 0 , è possibile trascurare l’ultimo
termine, per cui si ha:
α = 1+
(r1 − r2 ) + (R s
1
− R s2
)
R0
quindi l’incertezza assoluta diventa:
⎛ (r − r ) ⎞
1
1
uα = ⎜⎜ 1 2 2 ⎟⎟ ⋅ u R2 0 + 2 ⋅ u r21 + u r22 + 2 ⋅ u R2 S1 + u 2R S2
R0
R0
⎝ R0 ⎠
2
(
2
)
(
)
A volte il metodo di sostituzione viene utilizzato per misurare una resistenza incognita con
una incertezza più bassa di quella raggiungibile col metodo tradizionale, ma richiede
l’impiego di due resistori campioni variabili. Si posiziona la resistenza incognita nel ponte e si
raggiunge una prima condizione di equilibrio:
Rx =
Ra
⋅ R c1
Rb
Si sostituisce la resistenza incognita R x con un'altra resistenza campione variabile R c 2 e si
agisce solo su quest’ultima mantenendo fisso R c1 fino a raggiungere una nuova condizione
d’equilibrio:
Rc2 =
Ra
⋅ R c1
Rb
Confrontando i due equilibri, si deduce che:
R x = Rc2
Dal punto di vista della valutazione dell’incertezza, la relazione precedente può essere scritta
come:
R x = R c 2 + 2R s
in quanto essa è scaturita da due condizioni di equilibrio. Ne segue che l’incertezza assoluta è
data da:
u 2R X = u 2R C + 4u 2R S
per cui l’incertezza su R a e su R b non rientra in questa relazione e quindi la misura è
caratterizzata da un’incertezza minore rispetto al ponte tradizionale.
13