Facoltà di Ingegneria

Facoltà di Ingegneria
Prova scritta di Fisica I – NO & VO
01-07-03 - Compito A
Esercizio n.1
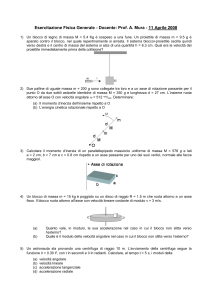
I blocchi A e B della figura hanno rispettivamente massa m A = 4kg ed m B = 8kg . Il blocco A è legato alla parete
verticale da un filo inestensibile, di massa trascurabile. Il coefficiente di attrito dinamico tra tutte le superfici vale
µ d = 0.25 .
Trovare il modulo della forza F (vedi figura) che occorre applicare al
blocco B per tenerlo in movimento verso sinistra con velocità costante.
Calcolare in tal caso la tensione del filo.
Supponendo poi che il blocco A venga saldato a B e che il filo venga
tagliato, si calcoli il nuovo modulo della forza F che occorre applicare
al blocco B per tenerlo in movimento verso sinistra con velocità
costante.
A
F
B
Rispondere quindi alle seguenti domande:
1. La forza di attrito dinamico tra i due blocchi ha modulo
A. 9,8 N (*)
B. 23,0 N
C. 56,4 N
D. 76,2 N
2. Il modulo della forza di attrito dinamico tra il blocco B e la superficie orizzontale ha espressione
A. µ d (m B − m A )g
B.
µ d (m B + m A )g (*)
C.
µdmAg
D. µ d m B g
Quando il blocco A è tenuto fermo dal filo ed il blocco B si muove verso sinistra con velocità costante, la
tensione del filo ha modulo
A. 1,03 N
B. 9,8 N (*)
C. 26,1 N
D. 46,5 N
4. Quando il blocco A è tenuto fermo dal filo ed il blocco B si muove verso sinistra con velocità costante, la
forza F applicata vale:
A. 11.2 N
B. 19,0 N
C. 39,2 N (*)
D. 58,1 N
5. Quando i blocchi A e B si muovono insieme verso sinistra (filo tagliato ed blocco A saldato a B), il modulo
della forza F applicata vale:
A. 2.3 N
B. 29,4 N (*)
C. 56,1 N
D. 76,9 N
Esercizio n.2
Un proiettile di massa m=5g viene sparato orizzontalmente in un blocco di legno, di dimensioni trascurabili e massa
M=3kg, fermo su una superficie orizzontale. Il coefficiente di attrito dinamico tra il blocco e la superficie orizzontale è
µ d = 0.20 .
Il proiettile rimane attaccato al blocco, che scivola di d=25 cm lungo la
M
superficie prima di fermarsi.
vp
m
Calcolare
• Il lavoro della forza di attrito tra il blocco di legno e la superficie
orizzontale durante lo spostamento del blocco di legno
• Il tempo impiegato dal blocco di legno per fermarsi
• La velocità con cui è sparato il proiettile
• L’energia dissipata dal proiettile nell’urto con il blocco di legno
3.
Rispondere quindi alle seguenti domande:
6. Nell’urto tra il proiettile ed il blocco di legno si conserva:
A. l’energia cinetica
B. l’energia meccanica
C. la quantità di moto (*)
D. nessuna grandezza fisica
7. Il lavoro della forza di attrito tra il blocco di legno e la superficie orizzontale durante lo spostamento del blocco
di legno vale
A. -30.65 J
B. -1945,61 J
C. -1,47 J (*)
D. -0.038 J
8. Il tempo impiegato dal blocco di legno per fermarsi
A. 50,2 s
B. 33,6 s
C. 14,8 s
D. 0,5 s (*)
9. La velocità con cui è sparato il proiettile vale
A. 30,7 m/s
B. 2540,9 m/s
C. 1120,4 m/s
D. 595,2 m/s (*)
10. L’energia dissipata dal proiettile nell’urto col blocco di legno vale
A. 10,6 J
B. 231,0 J
C. 884,3 J (*)
D. 1402,6 J
Esercizio n.3
Un blocco di massa M è fermo su un tavolo che ruota orizzontalmente con velocità angolare costante ω . Una corda
sottile, passando attraverso un foro praticato nel centro del tavolo, collega il blocco di massa M ad un blocco di massa
m, sospeso verticalmente (vedi figura). Il coefficiente di attrito statico tra il blocco di massa M ed il tavolo è µ ; l’attrito
tra la fune ed il lato del foro è trascurabile. La distanza
r
tra il foro ed il blocco di massa M è r. Entrambi i
ω
blocchi possono essere considerati punti materiali.
M
Calcolare
• Il massimo valore del raggio r, rmax , per il
quale il blocco di massa M rimane fermo
• Il minimo valore del raggio r, rmin , per il
quale il blocco di massa M rimane fermo
• Il modulo della tensione della fune per
r = rmax e r = rmin
m
• Il valore di r, indicato con ro , per il quale la
forza di attrito tra il tavolo ed il blocco di massa M è nulla.
• Il modulo dell’accelerazione normale e dell’accelerazione tangenziale del blocco M quando r = ro
Rispondere quindi alle seguenti domande:
11. Il massimo valore del raggio r, rmax , per il quale il blocco di massa M rimane fermo è
A.
rmax =
B.
rmax =
C.
rmax =
mg
Mω 2
mg + Mgµ
Mω 2
mgµ + Mg
(*)
Mω 2
mg
Mω
12. Il minimo valore del raggio r, rmin , per il quale il blocco di massa M rimane fermo è
D.
rmax =
A.
rmin =
B.
rmin =
C.
rmin =
D.
rmin =
mg − Mgµ
Mω 2
mgµ − Mg
(*)
Mω 2
Mgµ
Mω
Mgµ
Mω 2
13. Per r = rmax , la tensione della fune vale
A. T = mg (*)
B. T = Mg
C. T = µMg
D. T = µMg rmax
14. Per r = rmin , la tensione della fune vale
A. T = mg (*)
B. T = Mg
C. T = µMg
D. T = µMg rmin
15. Il valore di r per il quale la forza di attrito tra il tavolo ed il blocco di massa M è nulla è
mg + Mgµ
A. ro =
2 Mω 2
mg − Mgµ
B. ro =
2 Mω 2
C.
ro =
D.
ro =
A.
aN =
B.
aN
C.
aN
mg
Mω
mg
(*)
Mω 2
16. Il modulo dell’accelerazione normale del blocco M quando r = ro è
mg + µMg
m
µmg + Mg
=
M
mg
=
(*)
M
D. 0
17. Il modulo dell’accelerazione tangenziale del blocco M quando r = ro è
B.
mg + µMg
2m
at = g
C.
at =
A.
at =
D. 0 (*)
Altre domande
µMg
m
18. Un punto materiale si muove di moto rettilineo lungo l’asse x con velocità
v = kt con k = 2
m
e t in
s2
secondi. Al tempo t=0s, il punto materiale si trova nella posizione x o = x (t = 0 ) = 10m ; al tempo t=2s il punto
materiale si trova nella posizione
A. x = 8m
B. x = 10m
C. x = 12m
D.
x = 14m (*)
19. La figura rappresenta due carrucole di raggi r1 ed r2 collegate da una cinghia che non scivola su di esse. Se la
carrucola di raggio r1 ha accelerazione angolare α 1 , l’accelerazione angolare dell’altra carrucola vale
A.
α2 =
r1
α 1 (*)
r2
B.
α2 =
r2
α1
r1
C.
α2 =
r1
α1
r1 + r2
D. α 2 =
r1 + r2
α1
r2
r1
r2
20. Un disco orizzontale gira intorno al proprio asse con velocità angolare costante ω . Ad un certo istante un
piccolo frammento di massa m cade verticalmente sul disco e si attacca alla superficie di esso. Il modulo della
velocità angolare del disco:
A. rimane invariato
B. aumenta
C. diminuisce (*)
D. diventa nulla
21. Il centro di massa di un sistema costituito dalle masse puntiformi m 1 ed m 2 , con m 2 >> m 1 , poste a distanza
d, si trova:
d
A. sulla congiungete m 1 − m 2 a distanza da m 1
2
d
B. sulla congiungete m 1 − m 2 a distanza da m 1
4
C. sulla congiungete m 1 − m 2 , vicino ad m 1
D. sulla congiungete m 1 − m 2 , vicino ad m 2 (*)
22. Un disco, di massa m e raggio r, partendo da ferma da un’altezza h (vedi figura) rotola lungo una collina il cui
profilo è rappresentato in figura. Quando il disco arriva nel punto più basso A, la velocità del suo CM è (si
trascuri l’attrito dell’aria e l’attrito volvente)
A.
2gh
B.
1
gh
2
C.
1
gh
3
M,r
h
4
A
gh (*)
3
23. Un punto materiale di massa m si muove in un campo di forza centrale. Durante il moto si conserva:
A. la sua velocità
B. la sua quantità di moto
C. il suo momento angolare (*)
D. nessuna quantità fisica
24. Nel moto parabolico di un proiettile lanciato verso l’alto ad un angolo di 45°, nel punto di altezza massima, la
velocità ha
A. componente orizzontale nulla e componente verticale diversa da zero
B. componente orizzontale diversa da zero e componente verticale nulla (*)
C. entrambe le componenti nulle
D. entrambe le componenti diverse da zero
25. Un sassolino viene lanciato verticalmente verso l’alto. Nel punto di altezza massima, il sassolino ha
A. velocità ed accelerazione nulle
B. velocità ed accelerazione diverse da zero
C. velocità nulla ed accelerazione diversa da zero (*)
D. velocità diversa da zero ed accelerazione nulla
D.
26. I tre settori circolari in figura (1,2,3) sono corpi rigidi bidimensionali, omogenei, di uguale massa
(m1 = m 2 = m 3 = m ) e raggio (r1 = r2 = r3 = r ) . Detti I1 , I 2 , I 3 i loro momenti d’inerzia rispetto ad un asse
passante per O ed ortogonale al piano della
2
3
figura si ha
1
A. I1 = I 2 , I 2 = I 3 (*)
B.
27.
28.
29.
30.
I1 = 3I 3 , I 2 = 2I 3
r,
m
r,
m
I
I3
, I1 = 2
O
O
r, Or
2
3
m
I
2I
D. I1 = 3 , I1 = 2
3
3
L’accelerazione del centro di massa di un sistema di particelle dipende
A. soltanto dalla risultante delle forze interne
B. soltanto dalla risultante delle forze esterne (*)
C. soltanto dal momento risultante delle forze interne rispetto al CM
D. soltanto dal momento risultante delle forze esterne rispetto al CM
Il momento angolare di un corpo rigido QUALSIASI che ruota intorno ad un asse con velocità angolare ω è:
A. parallelo all’asse di rotazione
B. parallelo ed equiverso ad ω
C. perpendicolare all’asse di rotazione
D. ha sia una componente parallela che una componente ortogonale all’asse di rotazione (*)
Dato un sistema di particelle, la quantità di moto totale si conserva se:
A. la risultante delle forze esterne è nulla (*)
B. la risultante delle forze interne è nulla
C. il momento risultante delle forze esterne rispetto al CM del sistema è nullo
D. tutte le forze esterne e tutte le forze interne sono conservative
Una ruota di raggio R e massa M compie un moto di puro rotolamento su di un piano orizzontale. Il suo centro
di massa si sposta lungo il piano di ∆s . Il lavoro compiuto dalla forza di attrito statico f s durante questo
spostamento vale:
A. L = f s ⋅ ∆s
C.
I1 =
B.
L = Rf s ⋅ ∆s
1
m∆s 2
2
D. L = 0 (*)
31. Nel corpo rigido di massa M mostrato in figura, sia a la distanza tra un asse passante per il CM ed un asse
parallelo ad esso e passante per A. Siano I CM ed I A i momenti d’inerzia rispetto a
questi assi, si ha:
A. I CM = I A
A
CM
2
a
B. I CM = I A + Ma
C.
L=
C.
I CM = I A − Ma 2 (*)
D.
I CM = I A − M 2 a 2
Soluzione
Esercizio n. 1
Le forze orizzontali (vedi figura) che agiscono sul blocco B, quando il blocco A è legato alla parete dal filo, sono
la forza F applicata, diretta verso sinistra
la forza di attrito tra il blocco B e la superficie
orizzontale, FB , di modulo FB = µ d (m A + m B )g e
A
diretta verso destra
la forza di attrito tra il blocco B ed il blocco A, FA , di
modulo FA = µ d m A g e diretta verso destra
Se la velocità di B è costante, la risultante di queste forze è
nulla:
F + FA + FB = 0
F
x
FA
FB
B
Proiettando questa equazione sull’asse x si ottiene il valore di F:
F − FA − FB = 0
F = FA + FB = µ d m A g + µ d (m A + m B )g = 39,2 N
Nella stessa situazione, le forze orizzontali che agiscono sul blocco A sono (vedi figura)
la forza di attrito tra il blocco B ed il blocco A,
FA' = −FA (3° principio di Newton), di modulo
FA' = µ d m A g = 9,8N e diretta verso sinistra
A
la tensione T del filo, diretta verso destra.
F
Poiché il blocco A resta fermo, si ha
T + FA' = 0
che proiettata lungo l’asse x dà
FA'
x
T − FA' = 0
T = µ A m A g = 9.81
T
B
m
s2
Quando il filo è tagliato, le forze orizzontali agenti sul blocco B sono:
la forza F applicata, diretta verso sinistra
la forza di attrito tra il blocco B e la superficie orizzontale, FB , di modulo FB = µ d (m A + m B )g e diretta
verso destra.
Con lo stesso procedimento di sopra, si ottiene:
F + FB = 0
F − FB = 0
F = FB = µ d (m A + m B )g = 29,4 N
Esercizio n. 2
Il lavoro della forza di attrito tra il blocco di legno e la superficie orizzontale durante lo spostamento del blocco di legno
è
d
0
d
L A = f a ⋅ d s = − f a ds = −(m + M )gµ d ds = −(m + M )gµ d d = −1,47J
0
0
0
Questo lavoro è uguale alla variazione di energia cinetica E k del sistema proiettile più blocco (teorema dell’energia
cinetica):
1
∆E k = E kf − E ki = 0 − (m + M )v i2 = L A
2
Il sistema proiettile più blocco, immediatamente dopo l’urto del proiettile, ha quindi velocità
− 2L A
m+M
D’altra parte nell’urto proiettile-blocco, si conserva la quantità di moto, quindi detta v p il modulo della velocità iniziale
vi =
(orizzontale) con cui viene sparato il proiettile, si ha
mv p = (m + M )v i
Dopo
l’urto,
il
vp =
(m + M )v i
sistema
m
=
− 2L A (m + M )
m
= 595,25
blocco+proiettile
m
s
si muove di moto
µ(m + M )g
uniformemente accelerato, con accelerazione a = −
= µg .
m+M
L’equazione del moto del sistema è quindi:
1
x − x o = v o t − µgt 2
2
Essendo x − x o = d , si ha
t=
2d
= 0,5s
µg
m
vp
M
L’energia E d dissipata nell’urto è uguale alla variazione di energia cinetica durante l’urto:
1
(m + M )v i2 − 1 mv 2p = −L A − 1 mv 2p = −884,33J
2
2
2
L’energia E d può anche essere ottenuta applicando l’equazione del bilancio energetico al sistema proiettile+blocco:
E d = E kf − E ki =
Ef − Ei = LA + Ed
0−
dove
1
mv 2p = L A + E d
2
Ed = −
1
mv 2p − L A = −884,33J
2
E f è l’energia meccanica del sistema proiettile+blocco dopo che il blocco ha percorso la distanza d
E i è l’energia meccanica del sistema proiettile+blocco prima che il proiettile colpisca il blocco.
Esercizio n.2
Quando il blocco di massa M è fermo sul tavolo ruotante, anche il blocco di massa m è fermo (la rotazione su se stesso
non viene considerata essendo il blocchetto assimilato ad un punto materiale) ed ha quindi accelerazione nulla.
Applicando al blocco m l’equazione del moto, F = ma ,
rmax
proiettata su un asse verticale orientato verso l’alto, si ha:
T − mg = ma = 0 T = mg
T
M
dove T è il modulo della tensione della fune.
f
Sul blocco di massa M agiscono due forze orizzontali: la
tensione della fune T , il cui modulo è stato appena
calcolato, e la forza d’attrito, f . La somma vettoriale di
queste due forze deve essere uguale alla forza normale (o
centripeta) necessaria affinché il blocco M, solidale al
m
tavolo, percorra la traiettoria circolare di raggio r.
Quando r = rmax , il blocco tende ad allontanarsi
radialmente dal foro, quindi la forza di attrito, opponendosi al moto, è diretta verso il foro (vedi figura) ed ha quindi
verso concorde con quello la tensione T della fune.
L’equazione del moto, proiettata sull’asse radiale orientato verso il foro, si scrive:
Ma N = Mω 2 rmax = T + f = mg + µMg
da cui
mg + µMg
rmax =
Mω 2
Quando invece r = rmin , il blocco tende a scivolare verso il foro, e la forza di attrito è diretta verso l’esterno (vedi
figura) ed ha quindi verso discorde a quello della tensione T della fune.
L’equazione del moto, proiettata sull’asse radiale orientato verso il foro, si scrive in questo caso:
Ma N = Mω 2 rmax = T − f = mg − µMg
rmin
da cui
T
rmin =
mg − µMg
f
Mω 2
Quando la forza di attrito tra il tavolo ed il blocco di
massa M è nulla, ad r = ro , la forza normale sul blocco M
è proprio la tensione della fune, cioè
2
Ma N = Mω ro = T = mg
ro =
mg
m
Mω 2
ro è, come prevedibile, il punto medio tra r = rmin ed r = rmax .
I moduli dell’accelerazione normale e tangenziale del blocco M, quando r = ro , sono rispettivamente
a N = ω 2 ro =
mg
dω
=0
ed a t = ro
M
dt
M