FISICA a.a. 2009-2010
Prof. G. Della Valle
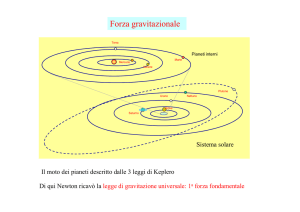
Gravitazione
1. La forza gravitazionale
1.1 Legge di gravitazione universale
Possiamo così esprimere la Legge di gravitazione universale formulata da Newton:
Due corpi qualsiasi, di masse m1 ed m2 e di dimensioni trascurabili rispetto alla loro
distanza, si attraggono con una forza diretta lungo la congiungente, di intensità
direttamente proporzionale al prodotto delle masse ed inversamente proporzionale al
quadrato della distanza:
!
mm
F = " ! 1 2 2 uˆr
r
ove ! = 6.67 "10 #11 m 3 kg #1s #2 è detta costante di gravitazione universale.
Oss.: La forza gravitazionale non richiede contatto fra i due corpi interagenti, ma agisce a
distanza; anzi, ha raggio d’azione infinito.
1.2 Verifica della legge di gravitazione universale
Storicamente, Isaac Newton nel 1666 formulò la legge di gravitazione universale come
spiegazione dinamica delle leggi di Keplero per il moto dei pianeti, e fece poi la prima
verifica della legge di gravitazione confrontando tra loro:
- l’accelerazione gravitazionale g sulla Terra
- l’accelerazione centripeta a L della Luna.
Infatti, se vale la legge di gravitazione universale si deve avere che l’accelerazione di gravità
F ( MT ,m,RT )
F ( MT ,mL ,rL )
M
M
= " 2T , mentre aL =
= " 2T
sulla Terra g =
m
RT
mL
rL
dove con RT abbiamo indicato il raggio della Terra e con rL il raggio dell’orbita lunare.
Stiamo inoltre considerando la Terra, nel calcolo di g, come se la sua massa fosse tutta
concentrata nel centro: non si tratta di un’approssimazione, ma ciò accade per tutti i corpi
!
!
sferici omogenei oppure con andamento della densità a simmetria sferica.
!
2
& rL #
g
!! , rapporto che non dipende né da ! , né da M T , ed è
Dunque, deve essere
= $$
aL
% RT "
piuttosto semplice da verificare, poiché delle quattro grandezze coinvolte:
- g può essere facilmente misurata con esperimenti sulla caduta dei gravi;
- a L si ricava da osservazioni astronomiche;
- RT è noto fin dall’antichità;
- rL era noto all’epoca di Newton con un certo grado di approssimazione, e per questo motivo
i suoi calcoli non quadravano esattamente.
Newton scelse allora di non pubblicare alcuno dei suoi risultati in attesa di un dato più
preciso, che confermasse la validità della sua legge. Trascorsero 20 anni prima che egli
pubblicasse le sue scoperte, era l’anno 1685, e l’opera (Philosophiae Naturalis Principia
1
FISICA a.a. 2009-2010
Prof. G. Della Valle
Mathematica) divenne così famosa da rivoluzionare non solo il pensiero scientifico ma anche
il pensiero di ogni intellettuale dell’epoca.
1.3 Misura della costante di gravitazione universale
Una misura abbastanza precisa della costante di gravitazione universale fu realizzata per la
prima volta dal fisico Cavendish nel 1798, mediante la bilancia di torsione. Due sfere di
piombo fisse attraggono due sferette più piccole vincolate tra loro da un’asticella molto
leggera ed appese ad un filo. L’attrazione provoca
una torsione del filo, fino a raggiungere un punto
di equilibrio in cui la forza di torsione bilancia
esattamente la forza di attrazione gravitazionale.
Dalla misura dell’angolo di torsione, fatta con
precisione grazie ad uno specchietto incollato sul
filo ed un raggio luminoso che, riflesso dallo
specchietto, incide su una scala graduata, si ricava
l’intensità della forza di torsione. Note le masse in
gioco e misurata la distanza si calcola la costante
di gravitazione universale. Il valore più preciso
Bilancia di torsione
noto oggi è:
# = 6.67 "10 !11 m 3 kg !1s !2
1.4 Massa inerziale e massa gravitazionale
Come conseguenza della legge di gravitazione universale abbiamo che ogni corpo possiede la
capacità di attrarre i corpi circostanti con un’intensità direttamente proporzionale alla propria
massa. In base alla legge di gravitazione, dunque, si può dare una definizione di massa
alternativa a quella data in dinamica: la grandezza caratteristica di un corpo che ne risulta
viene detta massa gravitazionale, indicata anche con m g . La massa inerziale mi , invece, è
definita come la costante di proporzionalità esistente tra la forza applicata ad un corpo e la sua
accelerazione (in un riferimento inerziale), e misura perciò la resistenza o inerzia di un corpo
alle variazioni del moto.
Sperimentalmente si verifica che sulla Terra tutti i gravi cadono con la stessa accelerazione di
gravità g, il che significa che il rapporto fra la loro massa gravitazionale, che influenza la
forza di attrazione verso la Terra, e la loro massa inerziale, che influenza l’accelerazione g, è
una costante.
Raffinati esperimenti hanno permesso di stabilire che, in tutti i fenomeni finora osservati,
esiste una rigorosa proporzionalità fra la massa gravitazionale e la massa inerziale. Risulta
legittimo, pertanto, imporre l’uguaglianza fra queste due grandezze ed utilizzare la stessa
unità di misura per entrambe (il kg).
1.5 Energia potenziale e potenziale gravitazionale
La forza gravitazionale generata da una massa puntiforme M è una forza centrale e quindi
conservativa; per introdurre la sua energia potenziale basta calcolare il lavoro compiuto dalla
forza gravitazionale per spostare una massa m da una distanza r dalla massa che genera il
campo ad un punto a distanza infinita, che prendiamo come stato di riferimento (ad energia
potenziale nulla).
2
FISICA a.a. 2009-2010
Prof. G. Della Valle
!
Mm
Mm
Mm
ˆ
u
%
dr
= & $! 2 dr = $ !
r
2
r
r
r
r
r
In base alla scelta fatta per il riferimento, l’energia potenziale gravitazionale risulta sempre
negativa: infatti la forza è attrattiva, quindi compie lavoro positivo per avvicinare le due
masse e lavoro negativo per allontanarle.
"
"
E p (r ) = E p (r )- E p (" ) = Lr #" = & $!
Potenziale gravitazionale
Definiamo ora, in ogni punto dello spazio, il potenziale gravitazionale come il rapporto tra
l’energia potenziale gravitazionale della massa m nel campo generato da M e la massa m
stessa:
E (r )
M
V ( r ) ! p, m
= "#
m
r
Il potenziale V è l’energia potenziale della massa unitaria, cioè il lavoro compiuto dalla forza
gravitazionale quando la massa unitaria si sposta dal punto considerato a distanza infinita
dalla massa M che genera il campo. Come l’energia, anche il potenziale è una grandezza
scalare; nel caso gravitazionale è negativo, come l’energia potenziale.
Potenziale generato da N masse puntiformi
Date N masse puntiformi M 1 , M 2 ,..., M 3 , il potenziale gravitazionale si calcola, in base al
principio di sovrapposizione degli effetti (valido per le forze, quindi per il lavoro, l’energia ed
il potenziale), come la somma dei rispettivi potenziali generati:
N
N
!
M
V ( r ) = !Vi ( ri ) = " # ! i
i=1
i=1 ri
Potenziale generato da un corpo esteso
Se conosciamo l’andamento spaziale della densità del nostro corpo esteso, che
schematizziamo come un sistema continuo, consideriamo anzitutto il potenziale generato in
!
!
un punto P ( r ) da un elemento di volume d" ! = dx !dy !dz ! in posizione P! ( r!) :
!
# ( r$) d% $
!
dV ( r ) = ! " ! !
r ! r$
Utilizziamo da ora in poi il simbolo ! (e non V) per i volumi, per evitare confusione con il
!
potenziale. Il potenziale gravitazionale generato da un corpo esteso in P ( r ) si ricava
!
$ ( r%) d& %
!
applicando il principio di sovrapposizione degli effetti: V ( r ) = ! dV = " # ! ! ! .
r " r%
corpo
corpo
1.6 Campo gravitazionale
L’interazione gravitazionale è una interazione a distanza, che non richiede il contato dei
corpi; in realtà, tuttavia, può essere descritta come una modifica dello spazio circostante
prodotta da una massa: ogni corpo genera un campo gravitazionale proporzionale alla sua
massa, e la forza gravitazionale agente su ogni corpo è pari al prodotto della massa del corpo
stesso per il campo generato da tutte le altre masse in gioco.
Def. Dunque possiamo dire che il campo gravitazionale generato da una massa M vale:
!
!
! !
F ( M , m, r )
M
G (r ) !
= " # 2 ûr
m
r
dove û r è il versore radiale uscente dalla massa M. Il campo è dunque diretto verso la massa,
come la forza; rappresenta infatti la forza agente su una massa unitaria.
3
FISICA a.a. 2009-2010
Prof. G. Della Valle
Le dimensioni dell’intensità del campo gravitazionale sono quelle di un’accelerazione.
!
Una massa m in un punto P ( r ) dello spazio sarà soggetta ad una forza gravitazionale:
!
! !
F = m ! G (r )
! !
dove il campo G ( r ) può anche essere prodotto da molte masse (anche estese). In questo caso
si applica naturalmente il principio di sovrapposizione degli effetti, cioè si esegue una somma
(vettoriale) dei singoli contributi. Il campo gravitazionale può essere rappresentato mediante
le linee di forza e le superfici equipotenziali.
Oss. Osserviamo che l’integrale di linea del campo gravitazionale da un dato punto
all’infinito coincide con il potenziale gravitazionale nel punto considerato:
#
# !
! #
!
!
M
M
M
$! G (r!) " dl = $! %& r!2 dr! = & r! ! = %& r = V (r )
r
r
r
Varrà dunque la seguente relazione differenziale (omologa della precedente relazione
! !
!
integrale): G ( r ) = !"V (r)
Oss. Tale risultato è l’ovvia conseguenza della conservatività della forza gravitazionale e
delle definizioni di campo e di potenziale gravitazionale (rispettivamente forza per unità di
massa ed energia potenziale per unità di massa). Infatti otteniamo immediatamente il risultato
precedente se dividiamo per la massa m ciascun termine nella seguente relazione già nota:
#
# !
! #
!
!
Mm
Mm
Mm
$! F (r!) " dl = $! %& r!2 dr! = & r! ! = %& r = E p (r )
r
r
r
! !
!
(e omologa relazione differenziale: F ( r ) = !"E p (r) ).
4
FISICA a.a. 2009-2010
Prof. G. Della Valle
2. Leggi di Keplero
Le leggi empiriche di Keplero
Nel II sec. d.C. Tolomeo di Alessandria propose il modello geocentrico dell’Universo, in cui
il Sole ruota intorno alla Terra. I pianeti descrivono orbite abbastanza complicate intorno alla
Terra (epicicli). Si tratta di un sistema complesso, ma capace di prevedere la posizione dei
pianeti.
Nel 1510 Niccolò Copernico propose il modello eliocentrico del Sistema Solare, in cui la
Terra e gli altri pianeti ruotano intorno al Sole. Utilizzava, in pratica, un sistema di
riferimento con buona approssimazione inerziale (solidale col Sole), che permette una
descrizione analitica molto più semplice del moto dei pianeti.
Sistema Tolemaico
Sistema Copernicano
Saturno
P
S
Giove
Epicicloide
TC
Terra
Luna
T CD
Deferente
Mercurio
Marte
Sole
Venere
L’astronomo danese Tyco Brahe (1546-1601) fece accurate osservazioni astronomiche del
moto dei pianeti; in base ai dati raccolti da Brahe, l’astronomo tedesco Johannes Kepler
(Keplero) (1571-1630) formulò le 3 leggi empiriche sulla cinematica del moto dei pianeti:
I. Ogni pianeta descrive un’orbita ellittica ed il Sole occupa uno dei due fuochi dell’ellissi.
II. Il vettore posizione di ogni pianeta rispetto al Sole descrive aree uguali in tempi uguali.
III. Il quadrato del tempo di rivoluzione di ciascun pianeta è proporzionale al cubo del
semiasse maggiore della sua orbita T 2 ! a 3 .
Dimostrazione delle leggi di Keplero
Le leggi di Keplero possono essere dedotte dalla teoria della dinamica del moto sotto l’azione
di una forza centrale che dipende dall’inverso del quadrato della distanza.
I.
La dimostrazione è piuttosto complessa ed è rimandata alla appendice.
II.
Si può facilmente dimostrare che la velocità areolare dA dt , cioè l’area spazzata dal raggio
vettore nell’unità di tempo, è costante.
y
P!
!
Sia m la massa del pianeta ed ! la sua velocità angolare
!
v
istantanea. Sappiamo allora che
dA
"
!
!
d$
P
L = m r 2! = cost # r 2
= cost.
d
!
dt
!
x
O
5
FISICA a.a. 2009-2010
Prof. G. Della Valle
1
1
r ! ( r d" ) = r 2 d"
2
2
(possiamo approssimare l’areola dA a quella di un triangolo che ha per altezza r e per base
l’arco di cerchio r d! )
Allora abbiamo che la velocità areolare risulta
dA
1 d!
1 L
S
= r2
=
= cost.
dt
2
dt
2m
(seconda legge di Keplero per il moto dei pianeti: il
raggio vettore spazza aree uguali in tempi uguali).
ma:
dA =
III.
Anche per la terza legge, nel caso generale di orbite ellittiche, si rimanda all’appendice.
Tuttavia per il caso di orbite circolari la dimostrazione è molto semplice.
Se esprimiamo l’area dell’orbita di raggio R come l’integrale della velocità areolare fatto su
un periodo di rivoluzione T (intervallo di tempo corrispondente ad un’orbita completa)
T
T
dA
1L
LT
2
avremo: ! R = A = "
, cioè LT = 2m! R 2 . Inoltre, per un generico
dt = "
dt =
2m
0 dt
0 2 m
!
k
moto circolare sotto l’azione di una forza centrale attrattiva F = ! 2 ûr , avremo, in base alla
R
!
!
I equazione cardinale della dinamica del punto materiale: F = ma
con
! !
2
a = aC = ! m" R ûr accelerazione centripeta.
2
k
Quindi ! 2 ûr = ! m" 2 R ûr # mkR = m 2" 2 R 4 # mkR = ( mR 2" ) = L2 cioè L = mkR .
R
Sostituendo l’ultima relazione trovata nell’equazione LT = 2m! R 2 abbiamo infine:
4! 2m 3
T2 =
R (terza legge di Keplero).
k
Particolarizzando poi l’espressione della forza centrale attrattiva al caso della forza
4! 2 3
gravitazionale, cioè ponendo k = ! Mm con (M la massa del Sole) abbiamo: T 2 =
R ,
"M
cioè la costante di proporzionalità tra T 2 ed R 3 è del tutto indipendente dal pianeta, quindi è la
stessa per ogni orbita.
6