Cognome, nome, matricola e firma . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Corso di Fondamenti di Meccanica - Allievi MECC. II Anno N.O.
II prova in itinere del 31 gennaio 2006
Esercizio di Meccanica Razionale
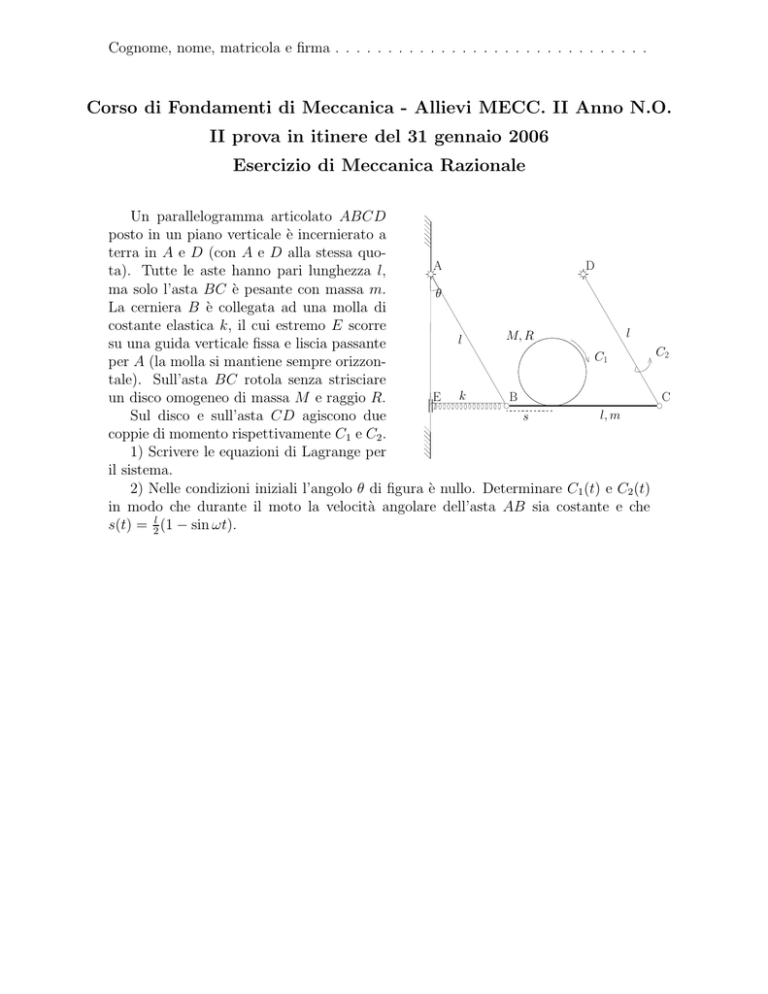
Un parallelogramma articolato ABCD
posto in un piano verticale è incernierato a
terra in A e D (con A e D alla stessa quoA
D
ta). Tutte le aste hanno pari lunghezza l,
ma solo l’asta BC è pesante con massa m.
θ
La cerniera B è collegata ad una molla di
costante elastica k, il cui estremo E scorre
l
M, R
l
su una guida verticale fissa e liscia passante
C2
C1
per A (la molla si mantiene sempre orizzontale). Sull’asta BC rotola senza strisciare
E k
B
C
un disco omogeneo di massa M e raggio R.
l, m
Sul disco e sull’asta CD agiscono due
s
coppie di momento rispettivamente C1 e C2 .
1) Scrivere le equazioni di Lagrange per
il sistema.
2) Nelle condizioni iniziali l’angolo θ di figura è nullo. Determinare C1 (t) e C2 (t)
in modo che durante il moto la velocità angolare dell’asta AB sia costante e che
s(t) = 2l (1 − sin ωt).
PSfrag replacements
Esame di fondamenti di meccanica
31 gennaio 2006 AA 2005-06
τ2, η2
τ1, η1
Jm
Jm
F
ho
V,a
M1
J1
O
G1
Rp
J2
L1
fv, fa
L
M2 G2
Ra
h
fv, fa
L2
fd
L3
A
Il veicolo in figura è mosso da un motore (momento di inerzia Jm) con asse longitudinale, che eroga una coppia
Cm=Co(1-ωm/ωo), ed aziona le ruote posteriore mediante due trasmissioni in serie (vedi riquadro) aventi rapporto di
trasmissione e rendimento rispettivamente τ1,η1, e τ2,η2. M1 ed M2 sono le masse del veicolo (baricentro G1) e della pala
(baricentro G2), incernierata al corpo centrale in O, posto a sua volta sulla verticale rispetto all’asse delle ruote anteriori,
e alla stessa altezza del baricentro G1. J1 e J2 sono i momenti di inerzia di ciascuna ruota anteriore e posteriore rispetto al
proprio asse di rotazione. F è una forza resistente nota applicata alla pala. Siano fv il coefficiente di attrito volvente delle
ruote sul terreno, fa il coefficiente di attrito di aderenza ruota-terreno e fd il coefficiente di attrito radente tra pala e
terreno.
Si consideri dapprima la cerniera in O bloccata (ossia agente come un incastro), e la pala non a contatto con il terreno,
ma con la forza F applicata. In tale configurazione ricavare:
1) l’espressione dell’accelerazione a del veicolo allo spunto;
2) la coppia motrice necessaria a regime;
3) la corrispondente velocità V del veicolo a regime
4) nella condizione del punto 1 ), effettuare la verifica di aderenza alle ruote posteriori;
Si consideri ora la condizione in cui la cerniera in O è sbloccata (agisce quindi come cerniera effettiva) con la pala a
contatto con il terreno (coefficiente fd agente) nel punto A.
In tale configurazione calcolare:
5) la coppia richiesta a regime
6) le reazioni vincolari nella cerniera O
RP = 0.6 m
M1 = 2500 kg
JP = 9 kgm2
τ1 = 1/6
η1 = 0.9
fd = 0.3
L = 3.5 m
L3 = 0.4 m
F = 1000 N
Ra = 0.3 m
M2 = 500 kg
Ja = 1 kgm2
τ2 = 1/2
η2 = 0.9
fv = 0.01
L1 = 1.5 m
h0 = 1 m
C0 = 100 Nm
Jm = 0.05 kgm2
fs = 0.6
L2 = 2 m
h1 = 0.3 m
ω0 = 476 rad/s
Fondamenti di Meccanica
Prova Scritta 14/2/2006
ESERCIZIO 1
C
Il sistema meccanico in figura, posto nel piano verticale, è formato dalle aste AC e AB, prive
di massa, dal corsoio di massa M vincolato a muoversi sulla guida orizzontale e dal disco di
centro B che rotola senza strisciare sulla guida verticale.
Il sistema è movimentato dalla coppia C che agisce sull’asta AC.
Nota la geometria del sistema e l’angolo α si chiede di:
1. determinare la relazione analitica tra la velocità del punto A ed α&
2. determinare la relazione analitica tra la velocità angolare del disco ed α&
3. scrivere potenza delle forze e coppie applicate al sistema
4. calcolare la coppia C in modo tale che α& =cost.
5. calcolare le reazioni vincolari in K
ESERCIZIO 2
In un piano verticale un filo è avvolto su una carrucola di massa m e raggio R incernierata a
terra. Un estremo del filo è attaccato ad una lamina quadrata di massa M e lato L che scorre
su una guida verticale fissa e liscia. L'altro estremo del filo si avvolge su una scanalatura
circolare di raggio R/2 concentrica e saldata ad un disco di massa 2m e raggio 2R
incernierato a terra nel suo centro. Un secondo filo si avvolge sulla periferia di questo
secondo disco ed al suo estremo libero è applicata una forza verticale F costante.
1. Determinare il rapporto tra le velocità angolari dei dischi.
2. Determinare la velocità della lamina in funzione del tempo.
3. Calcolare durante il moto le reazioni vincolari agenti sulla lamina nei punti A e B
Corso di Fondamenti di Meccanica – Allievi MECC. II Anno N.O.
14/02/2006
ESERCIZIO 4
C
M,R
ω
2R
F
s
m
In un piano verticale, un disco di massa M e raggio R rotola senza strisciare su una
guida orizzontale. Un’asta di lunghezza 2R e massa trascurabile è vincolata a cerniera
in un suo estremo al centro del disco e nell’altro estremo a un carrello che scorre
senza attrito sulla guida. Un anellino di massa m scorre senza attrito sull’asta.
Sul disco viene applicata una coppia di momento C(t) e sull’anellino una forza F(t)
parallela all’asta.
Si chiede di:
1. Scrivere le equazioni di Lagrange per il sistema.
2. Il sistema viene fatto partire dando al disco una velocità angolare ω0 e
all’anellino una velocità di scorrimento rispetto al centro del disco pari a
s& ( 0 ) =v 0 . Determinare C(t) e F(t) in modo che il modo si mantenga con ω(t)=
ω0 e s(t)=v0·t.
3. Determinare le reazioni vincolari esterne.
Esercizio 1
O
x, x& = cost
F
A
R
M
ϕ , ϕ& , ϕ&&
B
C
30°
D
AB = a
BD = b
m, r
H
Il sistema rappresentato in figura giace nel piano verticale. Il disco di massa m e raggio r rotola senza strisciare su una
guida ad arco di circonferenza avente raggio R. Determinare, in assenza di perdite per rotolamento tra disco e guida,
1.
2.
3.
4.
5.
la velocità angolare del disco in funzione di x&
l’accelerazione angolare del disco in funzione di x&
la potenza della forze/coppie attive
la forza F che garantisce il moto
le reazioni vincolari in H
Determinare quindi, in presenza di perdite per rotolamento,
6.
7.
la forza F che garantisce il moto
e verificare l’aderenza tra disco e guida
Esercizio 2
Corso di Fondamenti di Meccanica
Allievi MECC. II Anno N.O.
Appello del 4 luglio 2006
Nel sistema di figura il carrello ha massa m
P
M, R
e scorre senza attrito sulla guida orizzontale.
Su di esso rotola senza strisciare un disco di
massa M e raggio R. Un filo inestendibile si
m
avvolge senza strisciare sul disco e scorre senza
attrito su un piolo fisso P . All’estremo A del
A
filo viene applicata una forza verticale F(t).
1) Scegliere le coordinate libere ed esprimeF(t)
re l’energia cinetica del sistema in funzione di
esse.
2) Calcolare le componenti della sollecitazione attiva F(t) secondo le coordinate
libere.
3) Determinare la forza F(t) affinché l’accelerazione del carrello abbia un valore
costante prefissato a.
Fondamenti di Meccanica
Appello del 4 luglio 2006
O
&
60°
Cr
Cm
O1
s
B
30°
G
Jc
A
M, Jg
Il sistema articolato rappresentato in figura, disposto nel piano verticale, è costituito da una
manovella OA priva di massa che ruota con velocità angolare costante, da un glifo AB (massa M e
momento d’inerzia baricentrico Jg) e da un corsoio incernierato a terra in O1 (momento d’inerzia
baricentrico Jc). Nell’istante considerato il glifo è orizzontale. Sapendo che il baricentro del corsoio
coincide con la cerniera O1, determinare, nell’istante considerato:
1)
2)
3)
4)
5)
6)
7)
8)
la velocità angolare del glifo;
la velocità del baricentro del glifo;
l’accelerazione angolare del glifo;
l’accelerazione del baricentro del glifo;
la potenza delle forze e coppie esterne applicate al sistema;
la coppia motrice applicata alla manovella, in assenza di attrito radente tra glifo e
corsoio, che garantisce il moto;
le reazioni vincolari nella cerniera O.
la coppia motrice applicata alla manovella, in presenza di attrito radente tra glifo e
corsoio, che garantisce il moto;
Dati geometrici:
OA = r
AG = 1.5 r
OO1 = 3 r
Allievi MECC. II Anno N.O.
Corso di Fondamenti di Meccanica
Meccanica Razionale
Appello dell’8 settembre 2006
Il sistema di figura è posto in un
piano verticale. La lamina a forma
di triangolo equilatero ha massa m e
scorre senza attrito su di una guida
orizzontale. Il disco di massa M e raggio R rotola senza strisciare lungo un
lato della lamina.
Un filo inestendibile e di massa trascurabile si avvolge senza strisciare sul
disco. I due tratti liberi del filo HQ
e QA sono paralleli ai lati della lamina; il piolo liscio Q è solidale con la
lamina.
Sull’estremo A del filo viene esercitata
la forza F come in figura.
Q
H
m
M, R
A
F
x
1. Scegliere le coordinate libere del sistema e scrivere l’espressione dell’energia cinetica
in funzione di esse.
2. Scrivere le componenti delle sollecitazioni attive secondo le coordinate libere.
3. Scrivere le equazioni di Lagrange del sistema.
..
4. Determinare F affinché il disco salga con un’accelerazione angolare ϑ0 costante
assegnata. In tale situazione determinare il moto della lamina.
Esame di fondamenti di meccanica
8 settembre 2006. AA 2005-06
b1
Jm
b2
ωm τ, η
b3
A
V ,a
θ=30°
h/2
G
Motore
Riduttore ad assi ortogonali
leva
D
h
h/2
M
B
Il sistema in figura, posto nel piano verticale, è costituito da un motore che, mediante un riduttore
ad assi ortogonali, aziona un disco ed una leva considerati privi di massa e rigidamente connessi
all’albero di uscita del riduttore. La leva muove a sua volta un corsoio di massa M e baricentro G,
attraverso il punto D che si impegna in una guida rettilinea solidale con la leva. L’elemento di
massa M è vincolato ad una guida rettilinea verticale mediante due carrelli nei punti A e B.
Determinare, per un angolo generico θ:
1) il legame, in termini di funzione, tra la velocità angolare ωm del motore e la velocità V del
corsoio di baricentro G.
2) Il legame, in termini di funzione, l’accelerazione angolare del motore e l’accelerazione e la
velocità del corsoio di baricentro G.
Si consideri ora il sistema nella posizione in figura (θ = 30°) e nella condizione allo spunto;
determinare, nota l’accelerazione a della massa M:
3) la coppia motrice Cm necessaria;
4) le corrispondenti reazioni vincolari in A e B.
Si consideri ora il sistema nella stessa posizione, ma con velocità V non nulla diretta verso l’alto e
in presenza di attrito radente fd nei contatti con la guida in A e B:
5) calcolare le reazioni vincolari in A e B;
6) calcolare la coppia motrice Cm necessaria in questa nuova condizione.
Esame di fondamenti di meccanica
20 novembre 2006 AA 2006-07
Es1
s1
O
C
M1 ,J1
α , α& , α&&
H
F
M2
s2
A
Il sistema meccanico rappresentato in figura giace nel piano verticale ed è costituito da due corsoi e
da un glifo privo di massa. Il primo corsoio è incernierato a terra, il secondo trasla lungo una guida
orizzontale, il glifo è incernierato ad una sua estremità al centro del secondo corsoio e può scorrere
lungo il primo.
Determinare:
1. la velocità del secondo corsoio in funzione della velocità angolare del glifo;
2. l'energia cinetica e la potenza delle forze e delle coppie applicate;
3. la coppia applicata al primo corsoio che permette il moto nella configurazione assegnata;
4. la reazione vincolare nella cerniera A nella configurazione data.
M1 = 1 kg
J1 = 0.2 kgm2
M2 = 2 kg
H = 0.4 m
s1 = 0.01 m
s2 = 0.05 m
α = π/6
α& = 3 rad / s
F = 10 N
&& = 3 rad / s 2
α
Es2
Cm
s
A
B
F
H
θ
r
R
Un disco omogeneo di massa m e raggio R, posto nel piano verticale, rotola senza strisciare su una
guida orizzontale e fissa. Un secondo disco di massa m e raggio r (con r<R) e' RIGIDAMENTE
saldato nel centro del primo disco. Un'asta AB di massa M e lunghezza L è vincolata in A mediante
un carrello ad una guida orizzontale, ed è appoggiata con vincolo di puro rotolamento sulla
circonferenza del secondo disco. Una coppia oraria di momento Cm costante e nota è applicata al
primo disco e una forza F costante e nota è applicata nell’estremo B dell’asta.
Inizialmente il sistema è in quiete.
Si chiede di:
1. determinare la relazione tra la velocità assoluta dell'asta e la velocità angolare dei dischi;
2. scrivere l'espressione dell'energia cinetica del sistema e la potenza delle forze agenti;
3. determinare il moto del sistema;
4. calcolare il tempo necessario all’asta per compiere uno spostamento s = L/2.












