Piano di Lavoro annuale
Anno scolastico
Docente
Classe
Disciplina
Testo in uso
2016-2017
PAPAIOANNOU PARASKEVI
4E
14 alunni
MATEMATICA
3 ore settimanali
MATEMATICA.VERDE 2a edizione volume 4 (BERGAMINI,
TRIFONE, BAROZZI)
Finalità della
disciplina
Livello di partenza
rilevato
Metodologia per il
raggiungimento
degli obiettivi
Spazi, mezzi e
strumenti che si
prevede di
utilizzare
Attività di
recupero e
potenziamento
previste
Verifica e
valutazione
Promuovere le facoltà sia intuitive che logiche
Educare ai processi di astrazione
Sviluppare le attitudini sia analitiche che sintetiche
Sviluppare la capacità di utilizzare metodi, strumenti e modelli in situazione
Educare alla consapevolezza del valore della matematica quale componente culturale per la lettura ed interpretazione della realtà
Mediocre
Comportamento
Vivace ma corretto
Lezione frontale dialogata
Esercitazioni
Lavoro di gruppo - cooperative learning
Aula
Piattaforma online
LIM
Compiti svolti a casa
Didattica laboratoriale
Libri di testo
Dispense e fotocopie
Schede di lavoro
Recupero in itinere
interventi di potenziamento
Verifiche - Test
Prove scritte
Prove orali
Esercitazioni
Per la valutazione si terrà conto:
Del livello individuale di conseguimento degli obiettivi in termini di conoscenze e in termini di competenze.
Dei progressi compiuti rispetto al livello di partenza.
Dell’interesse, dell’impegno e della partecipazione al dialogo educativo.
Modulo
1. Disequa
-zioni
(di
primo e
secondo
grado)
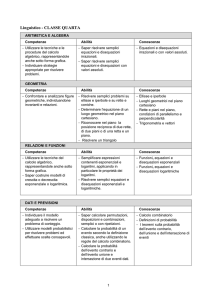
Competenze
-Costruire e
utilizzare modelli
-Risolvere
problemi
-Utilizzare
tecniche e
procedure di
calcolo
-Utilizzare le
tecniche e le
procedure del
calcolo
aritmetico ed
algebrico
rappresentand
ole anche
sotto forma
grafica
-Individuare le
strategie
appropriate per
la soluzione di
problemi
2. Equazioni e
disequa
-zioni
irrazionali e
con
-Utilizzare le
strategie del
pensiero
razionale negli
aspetti dialettici
e algoritmici per
affrontare
Abilità
-Risolvere e interpretare
graficamente disequazioni
lineari
Tempi
Da Settembre
a Ottobre
Obiettivi Minimi
-Studiare il segno di un
prodotto
Saper risolvere semplici disequazioni di I e
di II grado.
Saper risolvere semplici sistemi di
disequazioni.
-Studiare il segno di un
trinomio di secondo grado
-Risolvere disequazioni di
secondo grado intere e
rappresentarne le soluzioni
-Interpretare graficamente
disequazioni di secondo
grado
-Risolvere disequazioni
fratte
-Risolvere sistemi di
disequazioni in cui
compaiono disequazioni di
primo e secondo grado
-Utilizzare le disequazioni di
secondo grado per risolvere
problemi
-Applicare le disequazioni
per risolvere equazioni
irrazionali
-Risolvere equazioni e
disequazioni con valore
assoluto e irrazionali
Da Novembre
a Gennaio
Saper risolvere semplici equazioni e
disequazioni irrazionali con un solo
radicale
Saper risolvere semplici equazioni e
disequazioni con valore assoluto
valore
assoluto
3. Funzioni
situazioni
problematiche,
elaborando
opportune
soluzioni
- Risolvere
equazioni e
disequazioni
algebriche
-Utilizzare il
linguaggio e i
metodi propri
della matematica
per organizzare e
valutare
adeguatamente
informazioni
qualitative e
quantitative
- Individuare le principali
proprietà di una funzione
dominio, iniettività,
suriettività, biettività di
una funzione
- Rappresentare il grafico di
funzioni polinomiali,
esponenziali, logaritmiche
- Individuare parità disparità, crescenza –
decrescenza e segno di
una funzione
- Rappresentare il grafico di
funzioni polinomiali,
esponenziali, logaritmiche
Da Gennaio a
Marzo
Conoscere il concetto di funzione
Saper determinare i domini di funzioni
razionali, irrazionali, logaritmiche ed
esponenziali
Da Marzo a
Maggio
Saper determinare la parità e la disparità
di una funzione
Saper determinare gli intervalli di
positività e di negatività di una funzione
Anno scolastico
Docente
Classe
Disciplina
Testo in uso
2016-2017
PAPAIOANNOU
PARASKEVI
4E
14 alunni
COMPLEMENTI DI
MATEMATICA
1 ora settimanale
MATEMATICA.VERDE 2a edizione volume 4 (BERGAMINI, TRIFONE,
BAROZZI)
Modulo
1. Potenze ad
esponente
razionale
Competenze
-Utilizzare le
tecniche e le
procedure del
calcolo
aritmetico ed
algebrico
rappresentandol
e anche sotto
forma grafica
Abilità
-Rappresentare e
confrontare tra loro
numeri reali, anche con
l’uso di approssimazioni
-Applicare la definizione
di radice ennesima
-Determinare le
condizioni di esistenza di
un radicale
-Eseguire operazioni con i
radicali
-Semplificare espressioni
con i radicali
-Eseguire calcoli con
potenze a esponente
razionale
Tempi
Da Settembre a Ottobre
Obiettivi Minimi
Saper operare con le
proprietà delle potenze
ad esponente razionale
2. Equazioni e
disequazioni
esponenziali
3.Equazioni e
disequazioni
logaritmiche
- Utilizzare il
linguaggio e i
metodi propri
della matematica
per organizzare e
valutare
adeguatamente
informazioni
qualitative e
quantitative
- Individuare le
principali
proprietà di una
funzione
esponenziale
-Risolvere
equazioni e
disequazioni
esponenziali
- Utilizzare il
linguaggio e i
metodi propri
della matematica
per organizzare e
valutare
adeguatamente
informazioni
qualitative e
quantitative
- Risolvere
equazioni e
disequazioni e
logaritmiche
- Applicare le
proprietà dei
- Individuare le C.E. di
un’equazione
esponenziale
- Risolvere equazioni e
disequazioni
esponenziali
Da Novembre a Gennaio
Saper risolvere semplici
equazioni e disequazioni
esponenziali
- Risolvere espressioni
logaritmiche
- Risolvere equazioni e
disequazioni
logaritmiche
Da Febbraio a Maggio
Saper applicare le
proprietà dei logaritmi
Saper risolvere semplici
equazioni e disequazioni
logaritmiche
4.Statistica
Descrittiva
5.Teoria degli
errori
6.Distribuzione
Statistica dei
dati
logaritmi
- Analizzare dati e
interpretarli,
sviluppando
deduzioni e
ragionamenti
sugli stessi, anche
con l’ausilio di
rappresentazioni
grafiche, usando
consapevolmente
gli strumenti di
calcolo
- L’incertezza delle
statistiche e
l’errore standard
- Calcolo
approssimato
-Utilizzare i
concetti e i modelli
delle scienze
sperimentali per
investigare
fenomeni sociali e
naturali e per
interpretare i dati
-Appropriarsi del
concetto di
probabilità classica,
statistica
-Gli indici di
-Calcolare valori medi e
misure di variabilità di
una distribuzione
-Calcolare rapporti
statistici e interpretarne il
significato
7 ore da Dicembre a Gennaio
- Utilizzare tecniche e
procedure di calcolo
5 ore da Febbraio a Marzo
- Calcolare la probabilità
(secondo la concezione
classica)
di eventi semplici
-Analizzare e interpretare
dati e grafici
-Costruire e utilizzare
modelli
-Risolvere problemi
(ASL)
Valori medi e indici di
variabilità
Distribuzioni di frequenza
Rappresentazioni grafiche
dei dati
Errori sistematici e
casuali
Errore relativo ed errore
assoluto (anche
percentuale)
Precisione ed accuratezza
Cifre significative
Definizione di probabilità
classica (somma e
prodotto)
Distribuzione di Gauss
Campione e popolazione
Deviazione standard
Limiti di attendibilità
(ASL)
8 ore da Marzo a Maggio
variabilità: campo
di variazione,
scarto semplice
medio, deviazione
standard
Pozzuoli, 21/10/16
la docente Paraskevi Papaioannou