Esercizi Thevenin-regime sinusoidale e risonanza

Esercizio n°.1
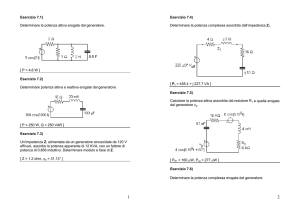
Con riferimento alla seguente rete in regime sinusoidale valutare:
1) Il circuito equivalente di Thevenin ai capi di R2
2) La corrente circolante in R2
3) La potenza complessa assorbita da R2
R1
L
ig(t)
eg(t)
C
a
R2
b
R1 =1.2
R2 =3.3
L = 3.2mH C = 4.1mF  = 1000 rad/s

ig (t )  2 sin(t  ) A
4

vg (t )  10 2 sin(t  ) V
3
Come primo passo, rappresentiamo il circuito nella forma che più si addice all’applicazione
del metodo simbolico, calcolando le impedenze dei diversi componenti e i fasori associati
alle forme d’onda dei generatori sinusoidali.
Si ha quindi:
zR1  R1  1.2
zR 2  R2  3.3
rad
 3.2  103 H  j3.2 
s
1
1
zC   j
j
  j 0.244
rad
C
3
1000
 4.1*10 F
s
zL  j L  j1000
Trasformiamo in coseno la forma d’onda del generatore di corrente:


ig (t )  2 sin(t  )  2 cos(t  ) A
4
4


vg (t )  10 2 sin(t  )  10 2 cos(t  ) V
3
6
Esprimiamo allora le forme d’onda associate ai generatori con i relativi fasori:

ig (t )  2 cos(t  )
4

vg (t )  10 2 cos(t  )
6
2
2
j
2
2
10 3
1
Vg  10  30 
j
2
2

Ig  1  45 

z R1
zL
a
I R2
Vg
Ig
zR2
zC
VR2
b
Calcoliamo l’impedenza equivalente di Thevenin alla porta a-b. A tale scopo passiviamo i
generatori indipendenti:
z R1
zL
a
zC
b
L’impedenza equivalente di Thevenin alla porta a-b è la serie dell’impedenza z L con
l’impedenza
z R1C data da:
zR1C 
Si ha quindi:
zR1 zC
zR1  zC
 0.05 - j 0.23
zTH  zR1C  zL  0.05  j 2.97
Per calcolare la tensione del generatore equivalente di Thevenin, valutiamo la corrente di
cortocircuito alla porta a-b:
z R1
Ig
Vg
zL
zC
a
I cc
b
A tale scopo valutiamo il contributo di ciascun generatore applicando la sovrapposizione
degli effetti. Il primo contributo che calcoliamo è quello del generatore di corrente, per cui
passiviamo quello di tensione:
I R1
z R1
zL
IL
a
VL
VR1
IC
Ig
zC
VC
I ccI
b
Applichiamo il partitore di corrente per calcolare il contributo I ccI alla corrente I cc dovuto al
generatore I g :
I ccI  I g
yL
 -0.068  j 0.043 A
yL  yC  yR1
A questo punto calcoliamo il contributo I ccV alla corrente I cc del generatore di tensione,
passivando quello di corrente:
z R1
zL
Vg
zC
VC
a
I ccV
b
Applichiamo il partitore di tensione alla serie costituita da z R1 e z LC , quest’ultima data da:
zLC 
zL zC
  j 0.264
zL  zC
essendo le impedenze z L e zC collegate in parallelo.
I R1
z R1
VR1
I LC
Vg
z LC
VLC
Si ha allora:
VLC  Vg
zLC
 -0.65 - j 2.05V
zR1  zLC
Ma essendo:
VLC  VL  VC
si ha:
I ccV  I L 
VL VLC

 -0.65  j 0.20 A
zL
zL
La corrente complessiva di cortocircuito è quindi data da:
I cc  I ccI  I ccV  -0.068  j 0.043 - 0.65  j 0.20  -0.71  j0.25 A
In definitiva la tensione del generatore equivalente di Thevenin è data da:
VTH  zTH I cc  -0.76 - j 2.09V
Per calcolare la corrente circolante in R2 sfruttiamo l’equivalente di Thevenin appena
calcolato:
zTH
I R2
VTH
zR2
VR2
Si ha:
I R2 
VTH
 -0.44 - j 0.24  0.5e  j 2.65 A
z R2  zTH
Nel dominio del tempo:
iR2 (t )  0.5  2 cos(1000t  2.65)  0.71cos(1000t  2.65) A
La potenza complessa assorbita da R2 è costituita dalla sola potenza attiva e vale:
2
N  VR2 I R2 *  z R2 I R2 I R2 *  z R2 I R2  0.82W
Esercizio n°.2
Determinare la pulsazione di risonanza del circuito in figura:
R
C
L
R = 200
L = 0.1H
C = 0.1F
Calcoliamo l’ammettenza y di ingresso del circuito.
Essa è data dal parallelo tra l’ammettenza y RL :
yRL 
1
R  j L
e l’ammettenza yC  jC .
Si ha quindi:
y  yRL  yC 
1
 jC
R  j L
Esprimiamo l’ammettenza y nella forma y  G  jB , separando quindi la conduttanza
dalla suscettanza:
y
1
1
R  j L
R  j L
 jC 

 jC  2
 jC
R  j L
R  j L R  j L
R   2 L2

y
R
j L
R
L 

 2
 jC  2
 j  C  2

2 2
2 2
2 2
R  L R  L
R  L
R   2 L2 

2
In condizioni di risonanza la suscettanza è nulla:
B  0C 
0 L
0
R 2  02 L2
A questo punto possiamo ricavare l’espressione ed il valore della pulsazione di risonanza
0 :
0C 
0 L
0
R 2  02 L2

CR2  C02 L2  L  0

L  CR 2
 
L2C
2
0

L CR 2
1
R2
0  2  2 

LC LC
LC L2

1
R 2C
1
2002  0.1 106
rad
0 
1

1
 9798
L
0.1
s
LC
0.1  0.1 106