Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
FISICA APPLICATA
Dott. Marta Ruspa
[email protected]
0321/660669
011/6707310
1
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
CORSO INTEGRATO DI
SCIENZE FISIOLOGICHE
Discipline:
FISICA APPLICATA
FISIOLOGIA (prof. Molinari)
2
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Le discipline di FISICA e FISIOLOGIA
possono essere sostenute separatamente
nei 4 appelli del 2012, ma entro settembre
va completato il corso integrato
Chi non completasse il corso integrato entro
settembre e avesse sostenuto una delle due
materie perdera’ la materia acquisita
Lezione I
3
Fisicaa Applicata, Area Infermieristica , M. Ruspa
APPELLI 2013
6 febbraio
21 febbraio
17 giugno
4 settembre
12 settembre
SARETE CONVOCATI IN ORARI DIVERSI
SEDE PER SEDE E CORSO DI LAUREA
Sara’ possibile registrare il corso integrato
in giorni prestabiliti (NON su appuntamento
individuale con i docenti)
Lezione I
4
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
ESERCITAZIONI
Sono previste ore di esercitazione dedicate per corso di laurea e
per sede (con docente dal vivo nelle varie sedi)
Calendario disponibile a breve
5
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MATERIALE DIDATTICO
Testo consigliato:
“Elementi di Fisica”
V. Monaco, R. Sacchi, A. Solano
Laurea Infermieristica
MC Graw Hill Editore
Altri testi indicati sul sito WWW descritto qui sotto
Pagina WWW aggiornata (con tutte le lezioni)
http://www.to.infn.it/~ruspa/didattica
raggiungibile anche come segue
Lezione I
6
Lezione I
7
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
8
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MATEMATICA DI BASE CHE
OCCORRE CONOSCERE
• Numeri relativi ed operazioni con i medesimi
• Frazioni
• Potenze e relative proprieta’
• Monomi, polinomi, espressioni algebriche
• Potenze di dieci e notazione scientifica
• Soluzione di equazioni di primo grado
• Proporzioni
• Percentuali
• Richiami di geometria piana e solida
• Conversioni tra unità di misura
Materiale del corso di potenziamento formativo sostenuto dagli
studenti di Infermieristica disponibile in rete - puo’ essere utile
anche come ripasso per chi non ha seguito il corso
Lezione I
9
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LA FISICA COME SCIENZA
SPERIMENTALE
Studio di un fenomeno
OSSERVAZIONI
SPERIMENTALI
IPOTESI
VERIFICA
LEGGI FISICHE
Lezione I
MISURA DI
GRANDEZZE FISICHE
Relazioni matematiche
tra grandezze fisiche
10
Lezione I
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CHE COSA E’
UNA GRANDEZZA FISICA?
11
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
CHE COSA E’
UNA GRANDEZZA FISICA?
TUTTO CIO’ CHE E’ MISURABILE
L’OPERAZIONE DI MISURA
DEFINISCE OPERATIVAMENTE
UNA GRANDEZZA FISICA
12
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GRANDEZZE FISICHE
CHE COSA SIGNIFICA MISURARE?
Confrontare la grandezza fisica in questione
con una grandezza campione di riferimento
Lezione I
13
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GRANDEZZE FISICHE
CHE COSA SIGNIFICA MISURARE?
Confrontare la grandezza fisica in questione
con una grandezza campione di riferimento
Espressione di una grandezza fisica:
Numero + unità di misura
Rapporto tra la grandezza e
il campione di riferimento
Lezione I
14
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GRANDEZZE FISICHE
CHE COSA SIGNIFICA MISURARE?
Confrontare la grandezza fisica in questione
con una grandezza campione di riferimento
Espressione di una grandezza fisica:
Numero + unità di misura
Rapporto tra la grandezza e
il campione di riferimento
Misura diretta:
Confronto diretto con il campione
(es. misura di lunghezza con un metro graduato)
Misura indiretta:
Misura di una grandezza legata a quella da misurare
attraverso una relazione nota
(es. misura di tempo con una clessidra)
Lezione I
15
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GRANDEZZE FISICHE
FONDAMENTALI
Tutte le grandezze fisiche possono essere espresse in funzione di un insieme
limitato di grandezze fondamentali
Grandezze fisiche fondamentali
Lunghezza
Tempo
Massa
Intensità di corrente
Temperatura
[L]
[t]
[M]
[i]
[T]
Un sistema di unità di misura definisce le grandezze fisiche fondamentali
e i corrispondenti campioni unitari (unità di misura). Le unità di misura
per le grandezze fisiche derivate si ricavano corrispondentemente
Lezione I
16
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SISTEMA INTERNAZIONALE (S.I.)
Grandezza
fisica fondamentali Unità di misura
Grandezze fisiche
Lunghezza
Tempo
Massa
Intensità di corrente
Temperatura
Lezione I
[L]
[t]
[M]
[i]
[T]
metro
secondo
chilogrammo
ampere
grado Kelvin
(m)
(s)
(kg)
(A)
(K)
17
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GRANDEZZE FISICHE DERIVATE
Le rimanenti grandezze fisiche sono derivate a partire dalle
grandezze fondamentali mediante relazioni analitiche (molte delle
quali studieremo in questo corso)
Alcuni esempi:
Superficie
(lunghezza)2
Volume
(lunghezza)3
Velocità
(lunghezza/tempo)
Accelerazione (velocità/tempo)
Forza
(massa*accelerazione)
Densità
(massa/volume)
Pressione
(forza/superficie)
...........
[L]2
m2
[L]3
m3
[L][t]-1
m·s-1
[L][t]-2
m·s-2
[M][L][t]-2kg·m·s-2
[M][L]-3
kg·m-3
[M][L]-1[t]-2
kg·m-2·s-2
Tutte le formule che studieremo nel corso andranno applicate dopo
aver espresso le varie grandezze fisiche nel S.I.
Lezione I
18
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
NOTAZIONE SCIENTIFICA
Grandezze fisiche molto grandi o molto piccole si possono
esprimere facendo uso della notazione scientifica
In notazione scientifica un numero si esprime come prodotto di
una cifra compresa tra 0,1 e 10 x una potenza di 10
5,738 · 103
19
Fisicaa Applicata, Area Infermieristica , M. Ruspa
NOTAZIONE SCIENTIFICA
Grandezze fisiche molto grandi o molto piccole si possono
esprimere facendo uso della notazione scientifica
In notazione scientifica un numero si esprime come prodotto di
una cifra compresa tra 0,1 e 10 x una potenza di 10
5,738 · 103
Esempi:
800 = ?
4765 = ?
l = 345000 m =?
l = 0,00038 m = ?
Massa della Terra = 5.980.000.000.000.000.000.000.000 kg = ?
Lezione I
Massa di un elettrone = 0,0000000000000000000000000000009109 kg
=?
20
Fisicaa Applicata, Area Infermieristica , M. Ruspa
NOTAZIONE SCIENTIFICA
Grandezze fisiche molto grandi o molto piccole si possono
esprimere facendo uso della notazione scientifica
In notazione scientifica un numero si esprime come prodotto di
una cifra compresa tra 0,1 e 10 x una potenza di 10
5,738 · 103
Esempi:
800 = 8·102
4765 = 4,765·103
l = 345000 m = 3,45·100000 m = 3,45·105 m
l = 0,00038 m = 3,8·0,0001 m = 3,8·10-4 m
Massa della Terra = 5.980.000.000.000.000.000.000.000 kg = 5,98·1024 kg
Lezione I
Massa di un elettrone = 0,0000000000000000000000000000009109 kg
= 9,11·10-31 kg
21
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
Grandezze fisiche molto grandi o molto piccole si possono
esprimere facendo uso della notazione scientifica
In alternativa o a complemento della notazione scientifica si
utilizzano multipli e sottomultipli
Le due soluzioni proposte sono legate perche’ i prefissi che
identificano multipli e sottomultipli corrispondono a varie
potenze di dieci
22
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MULTIPLI e SOTTOMULTIPLI
Prefisso
Simbolo Fattore di
moltiplicazione
Prefisso
Simbolo Fattore di
moltiplicazione
tera
T
1012
deci
d
10-1
giga
G
109
centi
c
10-2
mega
M
106
milli
m
10-3
kilo
k
103
micro
µ
10-6
etto
h
102
nano
n
10-9
deca
da
101
pico
p
10-12
Es: 1 m
1 km = 103 m
1 Mm = 106 m
1 Gm = 109 m
1 dm = 10-1 m
1 cm = 10-2 m
1 mm = 10-3 m
1 µm = 10-6 m
1 nm = 10-9 m
1 pm = 10-12m
(1 mm = 1/1000 m = 1/103 m = 10-3 m)
Lezione I
23
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Lezione I
Esercizi
103 l = 1 kl
103 m = 1 km
103 byte = 1 kbyte
1 µ = 10-6 m
57 Tbyte = 57 x 1012 byte
21 Mbyte = 21 x 106 byte
3 kg = 3 x 103 g
14 dm = 10-7 Mm
103 cl = 10 l
0.007 kPa = 7 Pa
220 mV = 0.22 V
2000 ohm = 2 kohm
157 kcal = 157000 cal
0.11 mA = 0.11 x 10-6 kA
24
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizi
98 mg/dl = 98 x 10-2 kg/m3
1.3 g/cm3 = 1.3 x 103 kg/m3
Il referto di un’esame del sangue riporta un V.E.S. di 72
mm/h. Si esprima la V.E.S. nel S.I. [R. 2 x 10-6 m/s]
Una cellula sferica ha il diametro di 20 µ. Qual e’ il
volume della cellula in cm3? [R. 4 x 10-9 cm3]
25
Fisicaa Applicata, Area Infermieristica , M. Ruspa
21 m/s = ? km/h
[R = 75,6 km/h]
1024 cm/min = ? km/s
[R = 17x1016 km/s]
10-6mm/min = ? m/s
[R = 17x10-12 m/s]
0.14 km/h = ?m/s
[R = 3.9x10-2 m/s]
26
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Alla stessa grandezza possono corrispondere unita’ di misura
differenti perche’ appartenenti a diversi sistemi di unita’ di misura
(per esempio il volume si puo’ misurare in litri e in m3)
Esistono unita’ di misura pratiche, utilizzate specificamente in certi
ambiti (medicina, meteorologia, …) Per esempio in ambito medico e’
d’uso esprimere le pressioni in mmHg e non nell unita’ di misura del
S.I. (che come vedremo si chiama Pascal)
Tutte le formule che studieremo nel corso andranno applicate dopo
aver espresso le varie grandezze fisiche nel S.I. , utilizzando le apposite
leggi di conversione
27
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FATTORI DI CONVERSIONE
1 l = 1 dm3
1 kcal = 4186 J
1 atm = 105 Pa = 760 mmHg
1 eV = 1.6 x 10-19 J
28
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LA FISICA COME SCIENZA
SPERIMENTALE
Studio di un fenomeno
OSSERVAZIONI
SPERIMENTALI
IPOTESI
MISURA DI
GRANDEZZE FISICHE
VERIFICA
LEGGI FISICHE
Relazioni matematiche
tra grandezze fisiche
In fisica si usa un linguaggio matematico !!!
29
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CHE COSA E’ UNA LEGGE FISICA?
Relazione matematica tra grandezze fisiche, ovvero uguaglianze
tra espressioni algebriche letterali in cui ogni grandezza e’
identificata da un proprio simbolo
1. Tutti i termini devono avere le stesse dimensioni fisiche
(monomi simili!)
2. Tutte le grandezze vanno espresse in un sistema di unita’ di
misura coerente
30
Fisicaa Applicata, Area Infermieristica , M. Ruspa
p + ½ dv2 + dgh = cost
31
Fisicaa Applicata, Area Infermieristica , M. Ruspa
p + ½ dv2 + dgh = cost
p e’ una pressione dv2 e dgh DEVONO
avere le DIMENSIONE FISICHE di una
pressione
p, dv2 e dgh DEVONO essere espressi in una
stessa unita’ di misura (es. Pa)
32
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GRANDEZZE SCALARI E VETTORIALI
Grandezze scalari:
caratterizzate da un numero
Es: tempo, temperatura, massa
Grandezze vettoriali: caratterizzate da un modulo, una direzione e un verso
Es: spostamento, velocità, accelerazione
direzione
verso
modulo
modulo del vettore v
: v = |v|
Es: |v| = 100 m/s
→
v
punto di
applicazione
Vettori uguali
Vettori opposti
33
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MECCANICA
Cinematica: moto dei corpi
Dinamica: cause del moto
Statica: equilibrio dei corpi
34
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MASSA e DENSITA’
Corpo: qualsiasi porzione di materia
35
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MASSA e DENSITA’
Corpo: qualsiasi porzione di materia
Massa: quantita’ di materia di un corpo.
>> Simbolo: m
>> Unita’ di misura nel S.I.: [kg]
36
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MASSA e DENSITA’
Corpo: qualsiasi porzione di materia
Massa: quantita’ di materia di un corpo.
>> Simbolo: m
>> Unita’ di misura nel S.I.: [kg]
Densita’: rapporto tra la massa e il volume
>> Simbolo: d
d = m/V
>> Unita’ di misura nel S.I.: [kg/m3]
37
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Considereremo il corpo come un punto materiale
nel quale e’ concentrata tutta la massa del sistema
Lavoreremo in un’unica dimensione, ovvero in
un sistema di riferimento unidimensionale
O
Attenzione: sul lbro di testo il moto e’ descritto
in 3 dimensioni
38
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POSIZIONE
P
O
39
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POSIZIONE
P
O
x
Unita’ di misura nel S.I.: [m]
40
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POSIZIONE
P
O
x
Unita’ di misura nel S.I.: [m]
Legge oraria
P1
t1
x1
P2
t2
x2
P3
t3
x3
x3
P3
x2
x1
P2
P1
t1
t2
t3
Funzione che esprime la variazione della posizione nel tempo
41
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SPOSTAMENTO
O
P1
P2
x1
x2
42
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SPOSTAMENTO
P1
O
x1
P2
x2 – x1
x2
Unita’ di misura nel S.I.: [m]
P1
t1
x1
P2
t2
x2
Δx = x2 – x1
Δt = t2 – t1
43
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SPOSTAMENTO
P1
O
x1
P2
x2 – x1
x2
Unita’ di misura nel S.I.: [m]
P1
t1
x1
P2
t2
x2
Δx = x2 – x1
Δt = t2 – t1
Traiettoria: ovviamente rettilinea, percorso
44
Fisicaa Applicata, Area Infermieristica , M. Ruspa
€
VELOCITA’ MEDIA vm
P1
O
x1
P2
x2 – x1
x2
Δx
vm = spostamento/ tempo =
Δt
P1
t1
x1
P2
t2
x2
Δx = x2 – x1
Δt = t2 – t1
Unita’ di misura nel S.I.: [m/s]
45
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ACCELERAZIONE MEDIA am
P1
O
x1
P2
x2 – x1
x2
Δv
a m = var.velocita'/ tempo =
Δt
P1
t1
x1
v1
P2
t2
x2
v2
Δx = x2 – x1
Δt = t2 – t1
Δv = v2 – t1
€
Unita’ di misura nel S.I.: [m/s/s] = [m/s2]
46
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Spesso, anziche’ riferirsi a due istanti t1 e t2, ci si riferisce ad
un istante iniziale t0 e ad un secondo istante qualsiasi t
t0
x0
v0
t
x
v
Δx = x – x0
Δt = t – t0
Δv = v – v0
47
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MOTO RETTILINEO UNIFORME
v = costante
a=0
v = cost
( x-xo)/t = cost
x = xo + v·t
48
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MOTO RETTILINEO UNIFORME
v = costante
a
v
t
a=0
v = cost
( x-xo)/t = cost
x = xo + v·t
t
x
xo
t
49
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MOTO RETTILINEO UNIFORME
Esempio:
v=5
m
s
xo = 3 m
Spazio percorso dopo Δt=10 s ?
€
a=0
v = cost
x = x0 + v·t
x= 3m + 5
m
⋅ 10 s = 53 m
s
€
50
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
a = costante
v - v0
t
→ v = vo + a ⋅ t
1
→ x = x o + vo t + at 2
2
a = cost =
€
51
Fisicaa Applicata, Area Infermieristica , M. Ruspa
€
MOTO RETTILINEO
UNIFORMEMENTE ACCELERATO
a = costante
a
t
v - v0
t
→ v = vo + a ⋅ t
1
→ x = x o + vo t + at 2
2
v
a = cost =
vo
t
x
xo
t
52
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SIAMO TUTTI UNIFORMEMENTE
ACCELERATI!
Tutti i corpi sulla Terra sono sottoposti
ad un’accelerazione costante verso il basso
(centro della Terra), che origina dall’attrazione
gravitazionale tra masse di cui parleremo
in seguito
53
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CADUTA IN UN GRAVE IN ASSENZA
DI ATTRITO
Accelerazione
di gravità
Vo = 0
a=g
v = g⋅t
h
x − x0 = h =
1
g⋅ t2
2
€
Esempio:
h = 10 m
54
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DINAMICA
55
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRINCIPI DELLA DINAMICA
I PRINCIPIO (PRINCIPIO DI INERZIA): un
corpo su cui non agiscano forze o la risultante delle
forze agenti sia nulla permane nel suo stato di
quiete o di moto rettilineo uniforme
56
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA
È quella grandezza fisica che,
applicata ad un corpo,
F
a) ne causa la variazione della
condizione di moto, oppure
b) ne provoca la deformazione.
È una grandezza vettoriale !
Esempio: composizione di due forze.
F1
R
F2
R è chiamata risultante delle forze
applicate al corpo.
57
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA
È quella grandezza fisica che,
applicata ad un corpo,
F
a) ne causa la variazione della
condizione di moto, oppure
b) ne provoca la deformazione.
È una grandezza vettoriale !
Esempio: composizione di due forze.
F1
R
F2
R è chiamata risultante delle forze
applicate al corpo.
58
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRINCIPI DELLA DINAMICA
II PRINCIPIO (LEGGE di NEWTON):
Forza =massa × accelerazione
F=m×a
Un corpo soggetto a una forza o a un insieme di forze a
risultante non nulla accellera proporzionalmente alla forza
applicata
>> Unita’ di misura nel S.I.: [kg x m/s2] = [N] Newton
1 N = 1 kg x 1 m/s2
59
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA DI GRAVITA’ o FORZA PESO
Forza peso = massa × accelerazione di gravita’
FP = m × g
FP
60
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DIFFERENZA TRA MASSA E PESO
ATTENZIONE alla differenza tra massa e peso: benche’ nel linguaggio
comune si utilizzino entrambi i termini con lo stesso significato
(riferendosi alla massa propriamente detta), in Fisica massa e peso
sono due grandezze differenti:
– la massa come visto e’ la quantita’ di materia di un corpo e si misura
in kg
– il peso come visto e’ una forza e si misura pertanto in Newton
– il peso di un corpo si ottiene dalla massa del corpo medesimo
moltiplicata per l’accelerazione di gravita’ g
61
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
Si determini il peso di 8 ml di mercurio
(densita’ del mercurio: 13.6 x 103 kg/m3)
[R. circa 1 N]
62
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA DI GRAVITA’ o FORZA PESO
Forza peso = massa × accelerazione di gravita’
FP = m × g
FP
Da dove origina la forza di gravita’?
63
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA DI GRAVITA’ o FORZA PESO
Forza peso = massa × accelerazione di gravita’
FP = m × g
FP
Forza di gravitazione
universale
m1 m 2
Fg = G
d2
m1
F
d
F
m2
€
64
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA DI GRAVITA’ o FORZA PESO
Forza peso = massa × accelerazione di gravita’
FP = m × g
FP
Forza di gravitazione
universale
m1 m 2
Fg = G
d2
m
m1
F
F
Terra mT
d
F
m2
€
65
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA DI GRAVITA’ o FORZA PESO
Forza peso = massa × accelerazione di gravita’
FP = m × g
FP
Forza di gravitazione
universale
m1 m 2
Fg = G
d2
m
m1
F
F
Terra mT
d
F
MT m
F = G 2
RT
m2
€
€
66
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA DI GRAVITA’ o FORZA PESO
Forza peso = massa × accelerazione di gravita’
FP = m × g
FP
Forza di gravitazione
universale
m1 m 2
Fg = G
d2
m
m1
F
F
Terra mT
d
F
m2
MT m
F = G 2
RT
€
g = 9,8 m/s2
€
67
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORZA DI GRAVITA’ o FORZA PESO
Forza peso = massa × accelerazione di gravita’
FP = m × g
FP
Forza di gravitazione
universale
m1 m 2
Fg = G
d2
m
m1
F
F
Terra mT
d
F
m2
€
g = 9,8 m/s2
68
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TANTI TIPI DI FORZE
Forza centripeta
Forza di reazione vincolare
Forza di attrito
Forza elastica
Forza elettrica
….
69
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LAVORO DI UNA FORZA
F
m
F
s
F
θ
F//
Δs
L = F// ⋅ Δs
>> Unita’ di misura nel S.I.: [N x m] = [J] Joule
€
1J = 1kg × 1m2/1s2
70
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LAVORO DI UNA FORZA
F
m
F
s
F
θ
F//
Δs
L = F// ⋅ Δs
La quantita’ di lavoro ottenibile da una
forza dipende dalla direzione relativa
della forza e dello spostamento
>> Unita’ di misura nel S.I.: [N x m] = [J] Joule
€
1J = 1kg × 1m2/1s2
71
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LAVORO DI UNA FORZA
F
m
F
s
F
F
θ
F//
Δs
L=F·Δs
Δs
L = F// ⋅ Δs
F
Δs
L=0
La quantita’ di lavoro ottenibile da una
forza dipende dalla direzione relativa
della forza e dello spostamento
>> Unita’ di misura nel S.I.: [N x m] = [J] Joule
€
1J = 1kg × 1m2/1s2
72
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LAVORO DI UNA FORZA
F
m
F
s
F
F
θ
F//
Δs
L=F·Δs
Δs
L = F// ⋅ Δs
F
Δs
L=0
La quantita’ di lavoro ottenibile da una
forza dipende dalla direzione relativa
della forza e dello spostamento
>> Unita’ di misura nel S.I.: [N x m] = [J] Joule
€
1J = 1kg × 1m2/1s2
73
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ENERGIA
•
Rappresenta la capacità che un corpo ha di compiere lavoro.
•
Concetto comune a molti campi della fisica, può presentarsi
in molteplici forme:
• energia associata a un corpo in movimento (energia cinetica)
• energia associata alla posizione di un corpo (energia potenziale)
• energia di legame molecolare (energia chimica)
• energia associata alla massa (energia nucleare, E=mc2)
• energia termica e calore
• .........
•
Ogni processo naturale coinvolge trasformazioni di energia.
•
In un sistema isolato l’energia totale si conserva sempre
(principio di conservazione dell’energia).
>> Unita’ di misura nel S.I.: [N x m] = [J] Joule
1J = 1N × 1m = 1kg × 1m/s2 × 1m = 1kg × 1m2/1s2
74
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ENERGIA POTENZIALE
GRAVITAZIONALE
Un corpo sollevato ad altezza
h possiede la capacita’ di
compiere lavoro in virtu’ del
proprio peso
Il lavoro di caduta si chiama
energia potenziale gravitazionale
e non e’ altro che il lavoro della
forza peso
75
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ENERGIA POTENZIALE
GRAVITAZIONALE
Un corpo sollevato ad altezza
h possiede la capacita’ di
compiere lavoro in virtu’ del
proprio peso
Il lavoro di caduta si chiama
energia potenziale gravitazionale
e non e’ altro che il lavoro della
forza peso
EP = LFP = F × s = F × h = mgh
76
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ENERGIA CINETICA
Un corpo che si muove a velocita’ v possiede in
virtu’ della sua velocita’ la capacita’ di compiere un
lavoro (per esempio se va a sbattere)
v
m
EC = ½ mv2
77
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizo
Si verifichi che l’unita’ di misura dell’energia potenziale
e dell’energia cinetica e’ il Joule
Si calcoli l’energia cinetica di un corpo di 27 kg che si
muove alla velocita’ di 120 km/h
[R. 14 x 103 J]
78
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POTENZA MECCANICA
La potenza rappresenta il lavoro compiuto
da una forza nell’unità di tempo
L
P=
Δt
>> Unita’ di misura nel S.I.: [J/s] = [W] Watt
1 W = 1J/1s
€
79
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FENOMENI ELETTRICI
80
Fisicaa Applicata, Area Infermieristica , M. Ruspa
L'atmosfera è continuamente sede di
fenomeni elettrici e magnetici che vanno
dal semplice accumulo di cariche
elettrostatiche alle scariche dei fulmini
durante i temporali
Nelle
giornate
secche
e
ventose
l'accumulo di cariche elettrostatiche sugli
abiti o sugli oggetti può portare alla
creazione di differenze di potenziale il cui
effetto si sente sotto forma di piccole
correnti
L’ipotesi e lo studio delle proprieta’ elettriche e magnetiche della
materia si sviluppo’ a partire dall’osservazione di questi fenomeni
che non trovavano spiegazione nella fisica allora nota (meccanica
classica)
81
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CARICA ELETTRICA
Tutto ciò che ha a che fare con l’elettricità trae origine da una
proprietà della materia chiamata carica elettrica (simbolo q)
In natura esistono due tipi di carica elettrica: positiva e negativa.
Sperimentalmente si osserva che cariche uguali si respingono,
cariche opposte si attraggono
>> Unita’ di misura nel S.I.: Coulomb [C]
82
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DOVE SI TROVA
LA CARICA ELETTRICA?
83
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DOVE SI TROVA
LA CARICA ELETTRICA?
NEGLI ATOMI
Elettroni
Nucleo
84
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DOVE SI TROVA
LA CARICA ELETTRICA?
NEGLI ATOMI
Elettroni
Nucleo
DI CHE COSA SIAMO FATTI?
85
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DOVE SI TROVA
LA CARICA ELETTRICA?
NEGLI ATOMI
Elettroni
Nucleo
DI CHE COSA SIAMO FATTI?
DI ATOMI
86
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FENOMENI ELETTRICI ALLA BASE
DELLA MATERIA VIVENTE E NON
Forze elettriche tengono
legati gli elettroni in un
atomo e gli atomi in una
molecola determinando le
proprieta’ chimiche di tutte
le sostanze
Elettroni
Nucleo
Nei sistemi biologici la forza elettrica
interviene nella trasmissione degli
impulsi nervosi, nella contrazione delle
fibre muscolari, nei meccanismi di
trasferimento cellulare
87
Fisicaa Applicata, Area Infermieristica , M. Ruspa
L’ATOMO
Nel suo stato normale, un atomo contiene lo stesso numero di protoni e di
elettroni, ed è quindi elettricamente neutro
Per esempio un atomo di ossigeno è costituito da un nucleo con 8 protoni
e 8 neutroni intorno a cui orbitano 8 elettroni. La carica sua totale è quindi
Q = 8x(1.6 10-19 C) + 8x(-1.6 10-19 C) + 8x0 C = 12.8 10-19 C - 12.8 10-19 C = 0 C
88
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CARICA ELETTRICA
Tutto ciò che ha a che fare con l’elettricità trae origine da una
proprietà della materia chiamata carica elettrica (simbolo q)
In natura esistono due tipi di carica elettrica: positiva e negativa
Sperimentalmente si osserva che cariche uguali si respingono,
cariche opposte si attraggono
>> Unita’ di misura nel S.I.: Coulomb [C]
La carica elettrica non si crea ne’ si distrugge ma si trasferisce
da un corpo all’altro
Corpi carichi: negativamente ⇒ eccesso di elettroni
positivamente ⇒ carenza di elettroni
Corpi neutri:
equilibrio tra cariche positive e cariche negative
89
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CARICA ELETTRICA DI UN CORPO
Poiché la carica elettrica Q di un corpo rappresenta un eccesso o un
difetto di elettroni, Q sarà sempre uguale ad un multiplo intero
(positivo o negativo) della carica dell’elettrone (qe)
|qe| = 1.6 · 10-19 C
Esercizio
Una bacchetta di vetro strofinata con un panno acquista una carica
elettrica Q=3.2·10-10 C. Quanti elettroni si trasferiscono dal vetro
al panno?
N= Q/|qe| =(3.2 · 10-10 C)/(1.6 · 10-19 C) = 3.2/1.6 · 10-10+19 = 2 · 109
90
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ELETTRIZZAZIONE DEI CORPI
Tale separazione di carica avviene per esempio quando sostanze
dissimili vengono strofinate una contro l’altra: se si strofina una
bacchetta di vetro con un tessuto di seta, alcuni elettroni si
trasferiscono dal vetro alla seta lasciando il vetro carico
positivamente e la seta negativamente
Altri esempi osservabili nella vita quotidiana:
se si fa scorrere vigorosamente un pettine tra i capelli asciutti
questi ultimi si elettrizzano
se strofiniamo su della lana un oggetto di plastica, esso si carica
elettricamente ed attira o respinge piccoli frammenti di carta 91
Fisicaa Applicata, Area Infermieristica , M. Ruspa
INTERAZIONE TRA CARICHE
- q2
+q1
+q2
- q1
Oggetti con carica dello stesso segno
si respingono
- q1
Oggetti con carica di segno opposto
si attraggono
+ q2
Questo vuol dire che oggetti carichi esercitano una forza l’uno
sull’altro
92
Fisicaa Applicata, Area Infermieristica , M. Ruspa
€
FORZA DI COULOMB
In analogia con la forza di gravitazione universale
m1 m 2
Fg = G 2
r
MA
•
la forza che agisce tra due cariche elettriche e’ molto piu’
intensa la costante deve essere molto piu’ grande di G
•
la forza che agisce tra due cariche elettriche e sia attiva
sia repulsiva (attiva se le cariche hanno segno opposto,
repulsiva se le cariche hanno lo stesso segno)
FCoulomb
q1q2
= k0 2
r
con
k 0 = 9 ⋅10 9 N ⋅ m 2 /C 2
nel vuoto
nella materia k < k0: la materia, essendo fatta di
cariche elettriche, scherma la forza di Coulomb
93
€
Fisicaa Applicata, Area Infermieristica , M. Ruspa
IONI
La perdita di uno o più e- trasforma gli atomi in ioni positivi
L’acquisizione di uno o più e- trasforma gli atomi in ioni negativi
e-
Na
Cl
94
Fisicaa Applicata, Area Infermieristica , M. Ruspa
IONI
La perdita di uno o più e trasforma gli atomi in ioni positivi
L’acquisizione di uno o più e trasforma gli atomi in ioni negativi
e-
Na
Sodio cede un elettrone al Cloro
Si formano così gli ioni Na+ e Cl-
Cl
95
Fisicaa Applicata, Area Infermieristica , M. Ruspa
IONI
La perdita di uno o più e trasforma gli atomi in ioni positivi
L’acquisizione di uno o più e trasforma gli atomi in ioni negativi
e-
Sodio cede un elettrone al Cloro
Si formano così gli ioni Na+ e ClAvendo carica opposta tali ioni si attraggono
Na
Cl
Si forma così un composto ionico detto
Cloruro di sodio (sale da cucina)
FE
Na+
Cl-
96
Fisicaa Applicata, Area Infermieristica , M. Ruspa
IONI
La perdita di uno o più e trasforma gli atomi in ioni positivi
L’acquisizione di uno o più e trasforma gli atomi in ioni negativi
e-
Sodio cede un elettrone al Cloro
Si formano così gli ioni Na+ e ClAvendo carica opposta tali ioni si attraggono
Na
Cl
Si forma così un composto ionico detto
Cloruro di sodio (sale da cucina)
FE
Na+
Cl-
• Ioni Na+ e Cl- si trovano anche nel plasma sanguigno
• Ioni Na+ e K+ giocano un ruolo fondamentale nella trasmissione
dell’impulso nervoso
97
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CORRENTE ELETTRICA
98
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CORRENTE ELETTRICA
Il moto ordinato di cariche elettriche all’interno di un materiale
è detto CORRENTE ELETTRICA. La corrente che scorre all'interno
di un corpo non e' qualcosa che viene dall'esterno: sono le
cariche elettriche contenute in quel corpo che si muovono
I = q/t
Intensita’ di corrente
>> Unita’ di misura nel S.I. : [A] Ampere 1A=1C/1s
99
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CONDUTTORI E ISOLANTI
Le proprieta’ elettriche di un corpo dipendono in modo
determinante dal fatto che siano disponibili o meno al
suo interno cariche elettriche libere di muoversi
100
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DIFFERENZA DI POTENZIALE
Affinche’ una o piu’ cariche si muovano tra due punti nello
spazio e’ necessario che tra i suddetti punti ci sia una
differenza di potenziale elettrico (simbolo ΔV)
Per comprendere il ruolo del potenziale elettrico e della
differenza di potenziale e’ utile l’analogia con il flusso
di acqua di un fiume. L’acqua (equivalente della carica
elettrica in questa analogia) scorre solo tra due punti
tra cui ci sia una differenza di altezza
>> Unita’ di misura nel S.I. : Volt [V]
101
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CIRCUITI ELETTRICI
Prendiamo due corpi, uno carico positivamente e l’altro
carico negativamente, tra cui esiste una differenza di potenziale
V1
+
-
V2
102
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CIRCUITI ELETTRICI
Prendiamo due corpi, uno carico positivamente e l’altro
carico negativamente, tra cui esiste una differenza di potenziale
V1
+
-
V2
Collegando i due corpi con un filo di materiale conduttore le
cariche negative si muoveranno verso il corpo carico
positivamente per azzerare la differenza di potenziale
V1
+
-
V2
103
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CIRCUITI ELETTRICI
Prendiamo due corpi, uno carico positivamente e l’altro
carico negativamente, tra cui esiste una differenza di potenziale
V1
+
-
V2
Collegando i due corpi con un filo di materiale conduttore le
cariche negative si muoveranno verso il corpo carico
positivamente per azzerare la differenza di potenziale
V1
+
-
V2
Collocando una lampadina lungo la strada delle cariche è
possibile accenderla
V1
+
-
V2
104
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CIRCUITI ELETTRICI
Per mantenere il moto delle cariche serve un generatore
di differenza di potenziale (ΔV)
Generatore di
+
differenza di potenziale DV
ΔV=V1-V2
Dispositivo
elettrico semplice
Spesso la differenza di potenziale viene anche chiamata
forza elettromotrice (f.e.m.) o tensione
105
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ESEMPI DI GENERATORI DI
TENSIONE
Pile
Batteria da 12V per
auto
L'elettricità che arriva nelle nostre case è prodotta in apposite
centrali elettriche e viaggia attraverso linee lunghe anche centinaia
di chilometri
106
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LEGGE DI OHM,
RESISTENZA ELETTRICA
Generatore
di tensione
(pila, dinamo, ..)
Resistenza elettrica R
(lampadina, stufa, ...)
I
+
-
ΔV
R
ΔV = R ⋅ I
>> Unita’ di misura nel S.I. : [Ω] ohm 1V= 1Ω × 1A
€
107
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CONDUTTORI E ISOLANTI
Le proprieta’ elettriche di un corpo dipendono in modo
determinante dal fatto che siano disponibili o meno al
suo interno cariche elettriche libere di muoversi
Resistenza elettrica di un conduttore:
l
l
R=ρ⋅
S
S
resistività:
- caratteristica del
materiale
- dipende dalla
temperatura
€
108
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
Una batteria con una differenza di potenziale di 1.5 V sviluppa
una corrente di 0.44 A che attraversa una lampadina per 64 s.
Trovare
a. la carica che scorre nel circuito
b. la resistenza della lampadina
[R. q = 28.16 C]
[R. R = 3.4 ohm]
109
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POTENZA ELETTRICA
Lavoro compiuto dalle forze elettriche per
portare una carica q da A a B:
I
A
+
-
?
ΔV
Potenza elettrica:
B
I
L’energia fornita dal generatore elettrico viene dissipata in R
sotto forma di calore (effetto Joule)
110
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esempio:
ENEL: Potenza installata: 3 kW=3·103 W
Si pagano: kWh
1 kWh = 103 W·3600 s =
= 103 W·3,6·103 s =
= 3,6·106 W·s = 3,6·106 J
111
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ENERGIA ELETTRICA
L’energia elettrica rappresenta una delle forme d'energia più
comunemente e diffusamente utilizzate: basti pensare alla luce
artificiale e agli elettrodomestici che sono presenti nelle nostre case
112
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CONDENSATORE PIANO
area A
+
+
ΔV
-
+ + + + + + + +
+ + + + + + +
+ + + + + + + + + + carica +Q
++
E
d
----------
carica -Q
Si accumulano cariche
elettriche sulle due piastre
creando una d.d.p.
-
isolante tra le
due armature
Condensatore a
facce piane e parallele:
Capacita’ elettrica C:
Unita’ di misura nel S.I.: [F] Farad 1F = 1 C/1V
113
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CONDENSATORE PIANO
Nota: - occorre compiere lavoro per caricare le due piastre A e B
(lavoro compiuto da un generatore
elettrico)
- l’energia accumulata puo’ essere poi usata
- utilizzato nei circuiti elettrici (simbolo
)
Nota: le membrane cellulari si comportano come un
condensatore !!
capacità C ≈ pF (10-12 F)
114
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CORRENTE ALTERNATA
La differenza di potenziale tra i due poli di una
comune presa di corrente e’ alternata, ovvero
presenta un andamento periodico con pocchi positivi
e picchi negativi (in Europa +-310 V a 50 Hz)
Si puo’ dimostrare che la
potenza media dissipata
nella resistenza e’ uguale
a quella che si avrebbe se
alla
resistenza
fosse
applicata una differenza
di potenziale costante di
220 V
115
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CONDUZIONE ELETTRICA NEL
CORPO UMANO
Il corpo umano è un buon conduttore elettrico perché nei suoi liquidi vi
è un’elevata concentrazione di ioni. La resistenza offerta al passaggio
di corrente dipende dai punti tra cui è applicata la tensione e dalle
condizioni: la pelle secca è isolante (R=2kW), se bagnata conduce
(R=2W)
Il passaggio di corrente può sviluppare calore, soprattutto nei punti in
cui la corrente esce ed entra dal corpo, e causare scottature e ustioni
Se la corrente attraversa la regione cardiaca possono prodursi
eccitazioni che interferiscono con l’attività di cuore e polmoni
Tempi di esposizione alla corrente brevi (< 1s) non sono in genere
pericolosi
116
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Conduzione elettrica nel corpo umano
Tempi di esposizione lunghi ad una corrente alternata con frequenza
50Hz possono dar luogo a:
I
~
1 mA
10 mA
70 mA
100÷200 mA
> 200 mA
ok
tetanizzazione dei muscoli
difficoltà di respirazione
fibrillazione
ustioni e blocco cardiorespiratorio
Se assumiamo per il corpo umano una R=2kW (pelle asciutta) il
contatto accidentale con la tensione alternata presente nelle nostre
case darebbe luogo ad una corrente:
Potenzialmente
mortale
Per questo nelle case ci sono dispositivi di messa a terra e un
interruttore salvavita che controlla la corrente che circola
nell’impianto e interrompe il circuito in pochi ms se riscontra anomalie
117
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FENOMENI MAGNETICI
118
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MAGNETISMO
Il magnetismo è un’altra delle proprietà fondamentali della materia
Alcune pietre (calamite naturali o
magneti) si attraggono a vicenda ed
attraggono materiali come il ferro o
l’acciaio
Un pezzo di acciaio temperato in
presenza di un magnete acquista
proprietà magnetiche che non
perde neppure quando lo si
separa dal magnete: diventa una
calamita permanente
119
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LA TERRA E’ UNA GRANDE
CALAMITA
Un ago calamitato libero di girare intorno al suo
centro (bussola) assume rispetto alla terra una
posizione definita, orientandosi lungo la
direzione nord-sud. L’estremità dell’ago che si
orienta verso Nord si chiama “Polo Nord” del
magnete. Analogamente è chiamata “Polo Sud”
l’estremità che si rivolge a Sud
Anche la Terra si
comporta come una grande
calamita
120
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POLI MAGNETICI
Qualunque magnete, come l’ago magnetico,
presenta un Polo Nord e un Polo Sud.
Se si spezza in due un magnete si
ottengono 2 magneti, ciascuno con un Polo
Sud e un Polo Nord. La stessa cosa accade
se dividiamo in due i “magnetini” ottenuti.
Fino ad oggi non si è ancora riusciti ad
individuare
un
oggetto
magnetico
costituito da un ‘unico polo
Il polo Nord di una calamita
respinge il polo Nord di un’altra
calamita, mentre attrae il suo Polo
Sud
Poli uguali si respingono
Poli opposti si attraggono
repulsione
attrazione
121
Fisicaa Applicata, Area Infermieristica , M. Ruspa
APPLICAZIONI MEDICHE DI
ELETTRITICITA’ e MAGNETISMO
Diverse sono le apparecchiature mediche che utilizzano campi
elettrici e magnetici a scopo diagnostico
ECG, EEG osservando le differenze di potenziale tra
diverse parti del corpo si traggono informazioni sul
funzionamento del cuore e del cervello
La risonanza magnetica utilizza campi
magnetici e onde radio per produrre
immagini tridimensionali degli organi
Defibrillatore: se alla regolare attività elettrica del
cuore subentra un’attività continua e anarchica si ha
fibrillazione
ventricolare
con
arresto
della
circolazione. Se il cuore in fibrillazione è
attraversato da una corrente elettrica intensa ma di
breve durata, le cellule cardiache vengono
simultaneamente depolarizzate e possono riprendere
il giusto ritmo.
122
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FENOMENI ONDULATORI
123
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ONDA
Oscillazione ma ... di che cosa?
Oscillazione della posizione,
velocità, accelerazione di un
mezzo materiale
ONDA ELASTICA (esempio:
onde del mare, onde sonore,
onde lungo una corda
vibrante)
Oscillazione dei vettori campo
elettrico e magnetico
ONDA
ELETTROMAGNETICA
si propaga anche nel vuoto
Se l’oscillazione si ripete ad intervalli regolari l’onda è detta
periodica
124
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LUNGHEZZA D’ONDA
Immaginiamo di fotografare una corda in oscillazione
otteniamo un’istantanea a tempo fissato
Lunghezza d’onda:
distanza tra due
massimi successivi; si
indica con λ (“lambda”)
e si misura in metri
125
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PERIODO
Immaginiamo di fissare sempre lo stesso punto di una
corda in oscillazione al trascorrere del tempo
otteniamo una ripresa a spazio fissato
Periodo: distanza tra
due massimi successivi;
si indica con T e si
misura in secondi
Frequenza: l’inverso del
periodo, f = 1/T, si
misura in secondi-1
126
Fisicaa Applicata, Area Infermieristica , M. Ruspa
VELOCITA’ DI PROPAGAZIONE
velocità = spazio/tempo
velocità = lunghezza d’onda/periodo
v = λ/T = λf
Si osservi che lunghezza d’onda e frequenza
sono inversamente proporzionali
127
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizi
Calcolare la frequenza corrispondente ad un’onda di periodo
T=10 msec.
Calcolare la corrispondente lunghezza d’onda sapendo che la
velocità di propagazione è v=340 m/s
128
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ONDE ACUSTICHE
ONDE ACUSTICHE:
compressione e rarefazione aria
‘onde di pressione’
Δp = Δpo sen(2 π ⋅ x λ )
• Se di frequenza compresa tra 20 Hz e 20000 Hz suono udibile
dall’orecchio umano
• Sotto i 20 Hz infrasuoni
€
• Sopra i 20000 ultrasuoni
Numerose applicazioni mediche, per esempio flussimetria Doppler e
ecografia a ultrasuoni
129
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ONDE ACUSTICHE
Materiale
Velocità di propagazione
Aria
344 m/s
Acqua
1480 m/s
Tessuto corporeo
1570 m/s
Legno
3850 m/s
Alluminio
5100 m/s
Vetro
5600 m/s
NOTA: Nel passaggio tra due mezzi con diverse velocità di propagazione,
la frequenza dell’onda si mantiene inalterata mentre varia la
lunghezza d’onda.
130
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POTENZA E INTENSITA’ SONORA
Potenza P di una sorgente [W]
È l’energia emessa da una sorgente (sonora) nell’unità di tempo
Intensità di un’onda I
[W/m2]
Rappresenta l'energia trasportata dall’onda che nell'unità di tempo
fluisce attraverso una superficie unitaria
L’intensità è inversamente proporzionale al quadrato della distanza
dalla sorgente
131
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
L’intensità di un’onda a 10 cm dalla sorgente è pari a 100 W/m2.
Calcolare l’intensità ad un metro di distanza dalla sorgente.
132
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LOG10
Il log10 di un numero qualsiasi a (base) e’ l’esponente che devo dare a 10 per
ottenere a
Il calcolo dei logaritmi si semplifica notevolmente quando la base e’ una
potenza di 10
log10 10n = n!
Infatti l’esponente che devo dare a 10 per ottenere 10n e’ n!
133
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DECIBEL
L’orecchio umano è sensibile ad intensità sonore tra 10-12 W/m2 e 102 W/m2.
Tuttavia, la sensazione uditiva non è proporzionale all’intensità sonora, ma
approssimativamente al suo logaritmo.
Livello di intensità sonora IL [dB]
E` definito come il logaritmo del rapporto fra l’intensità misurata ed una
intensità di riferimento (I0):
Per convenzione internazionale:
I0 = 10-12 W/m2 (minima intensità percepibile dall’orecchio umano)
10-12 W/m2 a 102 W/m2 → tra 0 e 140 dB
134
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esempi di intensità sonora
135
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ONDE ELETTROMAGNETICHE
Si può verificare sperimentalmente che
un campo elettrico variabile nel tempo produce un campo magnetico
un campo magnetico variabile nel tempo produce un campo elettrico
Campo magnetico variabile genera campo elettrico questo campo
elettrico è variabile e genererà un campo magnetico questo campo
magnetico è variabile e genererà a sua volta un campo elettrico variabile
…
Il Risultato è la
produzione di un’onda che si propaga nello spazio detta
onda elettromagnetica
136
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ONDE ELETTROMAGNETICHE
Tutte le onde em nel vuoto
si propagano con la stessa
velocità, pari alla velocità
della luce:
c= 3·108 m/s
La relazione tra lunghezza d’onda frequenza e velocità di propagazione
per un’onda elettromagnetica diventa:
c = λ/T = λ·f
137
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SPETTRO ELETTROMAGNETICO
All’ aumentare della lunghezza d’onda diminuiscono la frequenza e
l’energia
138
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SPETTRO ELETTROMAGNETICO
Come vengono utilizzate le onde elettromagnetiche
alle varie frequenze?
Scintigrafia
SPECT
Radiologia TAC
Radioterapia
139
Fisicaa Applicata, Area Infermieristica , M. Ruspa
UTILIZZO RAGGI GAMMA
DIAGNOSTICA: al paziente viene iniettato un radiofarmaco, ovvero
un farmaco marcato con un isotopo radioattivo emettitore di raggi γ
il paziente diventa una sorgente di raggi gamma, in particolare
i tessuti che metabolizzano il farmaco informazioni morfologiche
e funzionali
TERAPIA: radioterapia con fotoni (prodotti con acceleratori lineari)
140
Fisicaa Applicata, Area Infermieristica , M. Ruspa
UTILIZZO RAGGI X
141
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CALORE E TEMPERATURA
142
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Gli scambi di energia non necessariamente implicano
lavoro meccanico
contatto tra corpi a temperatura diversa
attrito
corrente elettrica attraverso una resistenza
reazioni chimiche
scambi energetici tra corpo umano e ambiente
circostante
• …
•
•
•
•
•
143
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MECCANICA i costituenti microscopici di un
corpo seguono le leggi introdotte moto d’insieme
(baricentro)
TERMODINAMICA i costituenti microscopici si
urtano casualmente e interagiscono reciprocamente
moto casuale, descritto da leggi statistiche
PARAMETRI MACROSCOPICI: p, V, T legati in modo
statistico alla posizione e velocita’ delle singole
molecole
144
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TEMPERATURA
Sensazione termica soggettiva
Definizione oggettiva?
Bisogna costruire una scala di riferimento basandosi
su fenomeni che avvengono sempre alla stessa
temperatura
145
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TEMPERATURA CELSIUS
0o C
ghiaccio in presenza di acqua di fusione
100o
acqua che bolle
TEMPERATURA FARENHEIT
32o F
ghiaccio in presenza di acqua di fusione
212o F
acqua che bolle
t(o C) = 5/9 [t(o F) -32]
146
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TEMPERATURA ASSOLUTA
V = V0 (1+αt) legge della dilatazione termica
t temperatura Celsius
gas perfetto α = 1/273.15 o C-1
t = -273.15 o C V-273.15 = V0 (1 + 1/273.15(-273.15)) = 0
un valore inferiore di temperatura implica un volume
negativo!
t = -273.15 o C
T(o
K) =
t(o
ZERO ASSOLUTO
C) + 273.15
t (o C) = 0 T (o K) = 273.15
t (o C) = 100 T (o K) = 373.15
147
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
Si trasformino 20o Faranheit in gradi centigradi e Kelvin
148
Fisicaa Applicata, Area Infermieristica , M. Ruspa
EQUILIBRIO TERMICO
Due corpi a temperature t1 e t2
(t2 > t1) sono posti in contatto
termico, isolati dall’ambiente
circostante
t1
t2
Dopo un certo tempo, i due
corpi raggiungeranno una
temperatura intermedia di
equilibrio tf
tf
tf
149
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TERMOMETRO CLINICO
Basato sull’equilibrio termico
Termometro ‘a massima’
La strozzatura tra il bulbo e il tubo capillare permette, sfruttando
la tensione superficiale, di conservare la lettura della temperatura
massima dopo la rimozione del termometro
150
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TEMPERATURA:
INTERPRETAZIONE MICROSCOPICA
Anche in assenza di un moto collettivo, gli atomi e le molecole di
un corpo sono in uno stato di moto caotico e disordinato. La
temperatura di un corpo e’ legata al livello medio di tale
agitazione termica della materia
Particella di un corpo solido, liquido o gassoso:
• Energia cinetica Ucin “agitazione termica”
• Energia potenziale Upot legami chimici
• Energia interna Ucin + Upot
Dalla combinazione di Ucin e Upot risultano i vari stati di
aggregazione della materia
151
Fisicaa Applicata, Area Infermieristica , M. Ruspa
STATI DI AGGREGAZIONE
SOLIDO: Upot >> Ucin
particella ordinate in struttura regolare
LIQUIDO: Upot ~ Ucin
le particelle fluiscono
GAS: Upot << Ucin
le particella si muovono in tutte le direzioni
152
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CAMBIAMENTI DI STATO
SOLIDO: Upot >> Ucin
particella ordinate in struttura regolare
Innalzando il livello termico aumenta Ucin liquido
(e viceversa)
LIQUIDO: Upot ~ Ucin
le particelle fluiscono
Innalzando il livello termico aumenta Ucin gas
(e viceversa)
GAS: Upot << Ucin
le particella si muovono in tutte le direzioni
153
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CAMBIAMENTI DI STATO
I cambiamenti di stato avvengono a temperatura costante
154
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CALORE
Nelle transizioni termiche viene scambiato calore
Quando due corpi a temperature diverse sono messi
a contatto viene trasferita energia termica dal corpo
piu’ caldo al corpo piu’ freddo il corpo piu’ freddo
guadagna Ucin e quindi sale in temperatura
Il calore puo’ essere ceduto o assorbito
>> Unita’ di misura nel S.I. : [J]
1 cal = 4.186 J
1kcal = 4186 J
155
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CAMBIAMENTI DI STATO
I cambiamenti di stato avvengono a temperatura costante
benche’ venga scambiato (ceduto o assorbito) calore che si
dice ‘calore latente’
156
Fisicaa Applicata, Area Infermieristica , M. Ruspa
METABOLISMO
157
Fisicaa Applicata, Area Infermieristica , M. Ruspa
METABOLISMO
Insieme delle reazioni biochimiche all’ interno
dell’organismo necessarie per il sostentamento delle
funzioni vitali e per l’attuazione di lavoro meccanico
verso l’esterno
Alimenti
Ossidazione
ALIMENTAZIONE
L’uomo e’
omeotermo
TERMOREGOLAZIONE
158
Fisicaa Applicata, Area Infermieristica , M. Ruspa
ALIMENTAZIONE
L’ossidazione delle sostanze organiche (carboidrati,
proteine e grassi) libera energia
Es.
C6H12O6 + 6O2 6 CO2 + 6 H2O + 666 kcal
Energia accumulata nei legami chimici della molecola di
ATP (adenosintrifosfato) e successivamente utilizzata
per il sostentamento dell’organismo e per l’attivita’
motoria
159
Fisicaa Applicata, Area Infermieristica , M. Ruspa
METABOLISMO BASALE
Minimo consumo energetico richiesto dai processi vitali:
• funzione cardiaca, respiratoria, ghiandolare e
nervosa
• tono muscolare
• mantenimento temperatura corporea
160
Fisicaa Applicata, Area Infermieristica , M. Ruspa
METABOLISMO ADDIZIONALE
•
•
•
•
Lavoro muscolare
Lavoro mentale
Digestione
…
TOTALE = BASALE + ADDIZIONALE ~ 2500 kcal/die
161
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POTENZA METABOLICA
MR “ Metabolic rate” kcal/tempo
BMR “Basal metabolic rate”
Parametro diagnostico importante determinabile per esempio con
uno spirometro attraverso la misura della quantita’ di ossigeno
consumato nella combustione delle sostanze in cui gli alimenti sono
scomposti
162
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LAVORO E POTENZA MUSCOLARE
Solo parte dell’energia impegnata viene trasformata
in lavoro utile
Rendimento η = lavoro utile/energia impegnata
= potenza meccanica/potenza
muscolare
In pratica il lavoro compiuto dai muscoli e’ molto
meno dell’energia impiegata dal nostro organismo per
farli funzionare
163
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POTENZA METABOLICA
MR “ Metabolic rate” kcal/tempo
BMR “Basal metabolic rate”
Parametro diagnostico importante determinabile per esempio con
uno spirometro attraverso la misura della quantita’ di ossigeno
consumato nella combustione delle sostanze in cui gli alimenti sono
scomposti
MR = BMR + potenza muscolare = BMR + potenza meccanica/η
164
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
Una persona a dieta svolge un’attivita’ fisica normale
consumando 2500 kcal/die mentre il suo regime alimentare
e’ di sole 1500 kcal. Se la differenza e’ compensata dai soli
grassi di riserva (1 g di grasso fornisce 9.3 kcal), di quanti kg
calera’ in un mese?
165
Fisicaa Applicata, Area Infermieristica , M. Ruspa
POTERE CALORICO
Proteine/zuccheri: 4.1 kcal/g
Grassi: 9.3 kcal/g
Quanti grammi di zucchero soddisfano il fabbisogno
metabolico totale di 2500 kcal?
166
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TERMOREGOLAZIONE
• Perdita di calore dall’epidermide
• Perdita di calore con vapore acqueo e aria espirata
• Evaporazione del sudore
Bassa temperatura ambiente (T<< 37 oC):
vasocostrizione, pelle d’oca, brividi
Alta temperatura ambiente (T ≥ 37 oC) o sforzo fisico:
vasodilatazione, sudore
167
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
Il calore latente di evaporazione dell’acqua a 37o C vale 580
cal/g. Si determini quanto calore viene smaltito attraverso
10 g di sudore
168
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MECCANICA DEI FLUIDI
Fluidostatica: fluidi in quiete
Fluidodinamica: fluidi in moto
169
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FORMA
VOLUME
SOLIDO
propria
proprio
LIQUIDO
contenitore
proprio
GASSOSO
contenitore
contenitore
FLUIDI
FLUIDI
masse densita’
forze pressioni
170
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRESSIONE
Pressione = forza/superficie
p = F/A
>> Unita’ di misura nel S.I.: [N/m2] = [Pa] Pascal
1 Pa = 1 kg / 1 m/ 1 s2
171
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRINCIPIO DI PASCAL
La pressione esercitata sun un punto della
superficie limite di un fluido si trasmette
inalterata in tutte le direzioni
172
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRESSIONE IDROSTATICA
Pressione esercitata in un punto in profondita’
dalla colonna di fluido che lo sovrasta
(pidr)P = Fp/A con
FP
A
peso colonna sovrastante A
superficie che contiene P
(pidr)P = d A h g/A = d g h
h
P
173
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRESSIONE IN UN FLUIDO IN QUIETE
p0
P
Quali e quante pressioni in P?
1) pressione esterna
(tipicamente pressione atmosferica)
2) pressione idrostatica
Pressione totale = p0 + dgh LEGGE di STEVINO
174
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRINCIPIO DEI VASI COMUNICANTI
In base alla legge di Stevino tutti i punti alla stessa profondita’
hanno lo stesso valore di pressione in
un sistema di vasi
comunicanti di qualsiasi forma la superficie limite si porta sempre
alla stessa altezza rispetto ad un piano di riferimento poiche’ la
pressione esterna, tipicamente la pressione atmosferica, e’ la
stessa in ogni punto della superficie
175
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRESSIONE ATMOSFERICA
Peso della colonna di aria che ci sovrasta di
altezza quindi pari all’altezza dell’atmosfera
patm = d g h con
d densita’ aria
h altezza atmosfera
176
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MISURA DELLA PRESSIONE
ATMOSFERICA: ESPERIMENTO DI
TORRICELLI
Condizione equilibrio:
Patm= pidr = dHg × 760 mm × g
patm
pidr
177
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MISURA DELLA PRESSIONE
ATMOSFERICA: ESPERIMENTO DI
TORRICELLI
L’esperimento di Torricelli dimostra che la pressione
atmosferica (a livello del mare) e’ pari alla pressione
esercitata da una colonna di mercurio alta 760 mm
Patm = pidrostatica (760 mm di Hg) =
= (si puo’ calcolare!) 1.013 x 105Pa
Si definiscono unita’ di misura pratiche:
pressione atmosferica a livello del mare =
= 1 atm = 760 mmHg ≈ 105 Pa
178
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
110 mmHg = ? Pa
179
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRESSIONE ATMOSFERICA
IN MONTAGNA e in PROFONDITA’
In montagna la pressione atmosferica diminuisce
poiche’ la colonna d’aria sovrastante le nostre teste
(atmosfera rimanente) e’ meno che a livello del
mare
Quando ci immergiamo in profondita’ nei mari la
pressione che agisce su di noi e’ maggiore che non a
livello del mare perche’ alla pressione atmosferica
si aggiunge la pressione dell’acqua che ci sovrasta.
Ogni 10 m di acqua procurano 1 atm!
180
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRESSIONE IDROSTATICA DEL
SANGUE
Anche una colonna di sangue possiede una pressione
idrostatica…quando siamo in posizione eretta
l’altezza dei nostri vasi sanguigni contribuisce una
pressione idrostatica che si somma (dal cuore in giu’)
e si sottrae (dal cuore in su) a quella cardiaca
181
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PRESSIONE IDROSTATICA DEL
SANGUE
La pressione cardiaca va sempre misurata con il
braccio del paziente all’altezza del cuore altrimenti la
pressione misurata sara’ la pressione cardiaca + o – il
contributo della pressione idrostatica di una colonna
di sangue di altezza Δh dove Δh e’ la differenza in
altezza tra il punto di misura e il cuore
Δh
(segno + se il punto di misura
e’ piu’ basso del cuore, segno
- se e’ piu’ alto)
182
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
Supponiamo una distanza tra il punto di misurazione e il
cuore di 30 cm. Di quanto si altera la misura della
pressione cardiaca a causa di tale distanza?
183
Fisicaa Applicata, Area Infermieristica , M. Ruspa
TERAPIE INFUSIVE
Per infondere farmaco in un vaso (vena) il farmaco
deve avere una pressione superiore a quella del sangue
nel vaso. Questa pressione si ottiene tipicamente
sollevando il contenitore nel farmaco rispetto al
punto di infusione. In questo modo per il farmaco di
ottiene una pressione idrostatica dgh dove d e’ la
densita’ del farmaco, g e’ l’accelerazione di gravita’ e
h e la differenza di altezza tra il farmaco e il punto
di infusione.
184
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
Per effettuare una terapia infusiva, a che altezza
minima va sistemato il recipiente affinche’ il farmaco
entri in una vena dove la pressione del sangue e’ 18
mmHg?
185
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MOTO DI FLUIDI IDEALI
• Non viscosi, incomprimibili
• Condotti a pareti rigide non deformabili
• Moto stazionario: velocita’ costante punto per punto
186
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PORTATA
La grandezza fisica che caratterizza il moto di un
fluido (si pensi per esempio ad un fiume) e’ la portata
definita come il volume di fluido che attraversa una
sezione del condotto di scorrimento nell’unita’ di
tempo
Q = V/t
>> Unita’ di misura nel S.I.: m3/s
Si puo’ dimostrare che
Q = S × v con
- S sezione trasversa condotto
- v velocita’ di scorrimento
187
Fisicaa Applicata, Area Infermieristica , M. Ruspa
LA PORTATA SI CONSERVA!
La massa di fluido che attraversa in un certo intervallo
di tempo la sezione di un condotto e’ la stessa che passa
in qualsiasi sezione nello stesso tempo, cioe’ poiche’ la
massa si conserva la portata si conserva, Q = cost
2
1
Q = cost Q1 = Q2
S1 v1 = S2 v2
Q1
Q2
Eq. di continuita’
188
Fisicaa Applicata, Area Infermieristica , M. Ruspa
EQUAZIONE DI CONTINUITA’:
RAMIFICAZIONI DI UN CONDOTTO
S1 v1 = S2 v2 = 5 S3 v3
189
Fisicaa Applicata, Area Infermieristica , M. Ruspa
EQUAZIONE DI BERNOULLI
Si dimostra a partire dalla conservazione dell’energia
meccanica
p1
p2
P + ½ dv12 + dgh = cost
p1 + ½ dv12 + dgh1 = p2 + ½ dv22 + dgh2
p1 + ½ dv12 = p2 + ½ dv22 per vaso orizzontale, h1 = h2
190
Fisicaa Applicata, Area Infermieristica , M. Ruspa
APPLICAZIONE DELL’EQUAZIONE
DI BERNOULLI: ANEURISMA
Aneurisma: ingrossamento di
un vaso S2 > S1
S1
S2
Se S2 > S1 per l’equazione di continuita’ v2 < v1
in un aneurisma la velocita’ del sangue diminuisce
Se v2 < v1 per il teorema di Bernoulli p2 > p1
in un aneurisma la pressione del sangue aumenta
191
Fisicaa Applicata, Area Infermieristica , M. Ruspa
APPLICAZIONE DELL’EQUAZIONE
DI BERNOULLI: STENOSI
Stenosi: restringimento di un
vaso S2 < S1
Se S2 < S1 per l’equazione di continuita’ v2 > v1
in una stenosi la velocita’ del sangue aumenta
Se v2 > v1 per il teorema di Bernoulli p2 < p1
in una stenosi la pressione del sangue diminuisce
192
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercizio
In un vaso sanguigno si forma un aneurisma dove la
sezione aumenta del 15%. Si calcoli la conseguente
variazione percentuale della velocita’ del sangue
193
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercitazioni Infermieristica
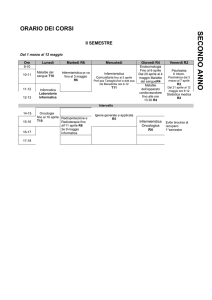
Novara: Gruppo A 28/1 9-13 29/1 14-18
Gruppo B 28/1 14-18
29/1 9-13
Alba
7/12/2012 11-13 14-17
25/01/2013 15-18 a Novara Alessandria 18/12/2012 10-13 14-16
14/01/2013 10-13 a Novara
Tortona 21/12/2012 11-13 14-17
25/01/2013 15-18 a Novara
Biella 6/12/2012 10-13 14-16
8/1/2013 10-13 a Novara
Verbania 29/11/2012 14-17
10/12/2012 16-18
7/01/2013 10-13 Novara
194
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercitazioni Infermieristica Pediatrica
26/11/2012 16-18
14/12/2012 14-16
le altre 4 ore sono da decidere per il mese di gennaio.
195
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Esercitazioni Ostetricia
30/11/2012 16-18
06/12/2012 15-17
le altre ore sono da decidere per il mese di gennaio.
196
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MOTO DI FLUIDI REALI
197
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MOTO DI UN FLUIDO REALE
Consideriamo un condotto orizzontale a sezione costante
1
2
S1 = S2 per l’equazione di continuita’ v2 = v1
v2 = v1, h2 = h1 per il teorema di Bernoulli p2 = p1
MOTO perpetuo a pressione e velocita’ costante!
Non esiste nella realta’!
L’equazione di Bernoulli va corretta
198
Fisicaa Applicata, Area Infermieristica , M. Ruspa
COME CORREGGERE BERNOULLI?
L’equazione di Bernoulli esprime come detto la
conservazione dell’energia meccanica, ovvero
(Emeccanica)1=(Emeccanica)2
Nella realta’ l’energia meccanica non si conserva
a causa dell’attrito
(Emeccanica)1=(Emeccanica)2 + attrito
Quindi tornando al condotto orizzontale a sezione
costante
p1 = p2 + attrito, ovvero Δp = attrito
199
Fisicaa Applicata, Area Infermieristica , M. Ruspa
PERDITA DI CARICO
E’ NECESSARIA UNA DIFFERENZA DI PRESSIONE
Δp PER VINCERE LE FORZE DI ATTRITO E FAR
SCORRERE FLUIDO IN UN CONDOTTO
ORIZZONTALE A SEZIONE COSTANTE
serve Δp = motore
ALTRIMENTI DETTO, LE FORZE DI ATTRITO
PORTANO ALLA CADUTA DELLA PRESSIONE IN
UN CONDOTTO (PERDITA DI CARICO)
Il nostro cuore e’ il motore del sangue!
200
Fisicaa Applicata, Area Infermieristica , M. Ruspa
RESISTENZA IDRODINAMICA
In analogia con la resistenza elettrica R = ΔV/I,
dove ΔV mette in moto le cariche e I e’ la carica
nell’unita’ di tempo
resistenza idrodinamica R = Δp/Q,
dove Δp mette in moto il fluido e Q e’ il volume di
fluido nell’unita’ di tempo
>> Unita’ di misura nel S.I.: [Pa s/m3]
R e’ direttamente proporzionale
- alla viscosita’ η
- alla lunghezza del condotto utilizzato
201
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CIRCUITO IDRODINAMICO DEL
SANGUE
Due condotti in serie
attraversati dalla
stessa portata
In media la portata
vale 5 litri/minuto
ovvero 83 cm3/s
(numero da ricordare
a memoria!)
202
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CIRCUITO IDRODINAMICO DEL
SANGUE
Tra piccola e grande circolazione la portata e’ la stessa
ma cambia la resistenza idrodinamica (maggiore lunghezza
del condotto)
Maggiori cadute di pressione nella grande circolazione
(LA PRESSIONE NELLE VENE E’ MOLTO PIU’ BASSA CHE
NELLE GRANDI ARTERIE)
Maggiore lavoro del cuore sinistro
Maggiore pressione in aorta che in arteria polmonare
203
Fisicaa Applicata, Area Infermieristica , M. Ruspa
Al momento dell’immissione dal ventricolo sinistro
all’aorta la pressione del sangue e’ in media un
centinaio di mmHg
Nella vena cava, che e’ l’ultimo vaso prima dell’atrio
destro, la pressione scende quasi fino a 0 (4 mmHg)
Il ventricolo destro ricomprime il sangue ad una
pressione di circa 25 mmHg prima dell’immissione
nell’arteria polmonare
Il sangue affluisce all’atrio sinistro a pressione quasi
nulla
A ciascun organo irrorato compete una resistenza idrodinamica.
La resistenza idrodinamica totale e’ la somma di tutti i distretti
204
Fisicaa Applicata, Area Infermieristica , M. Ruspa
IL SANGUE E’ VISCOSO, PERCHE’?
A causa dei globuli rossi soprattutto, che sono i piu’
grandi e i piu’ numerosi
La viscosita’ del sangue dipende
- dalla concentrazione di globuli rossi (ematocrito)
- dalla temperatura (aumenta al diminuire della
temperatura)
205
Fisicaa Applicata, Area Infermieristica , M. Ruspa
FREQUENZA CARDIACA
Numero di “battiti” (contrazioni ventricolari) al minuto
206
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GITTATA SISTOLICA
Volume di sangue immesso in aorta a ogni pulsazione.
Quanto vale in media?
207
Fisicaa Applicata, Area Infermieristica , M. Ruspa
VELOCITA’ DEL SANGUE
Con l’equazione di continuita’, a partire dalla portata e
dalla sezione dell’aorta, possiamo stimare la velocita’ del
sangue in aorta. Possiamo fare altrettanto per i capillari.
208
Fisicaa Applicata, Area Infermieristica , M. Ruspa
GAS, SOLUZIONI DILUITE,
FENOMENI DIFFUSIVI
209
Fisicaa Applicata, Area Infermieristica , M. Ruspa
MISCELA DI GAS
Sia data una miscela di gas in un recipiente di volume V a temperatura T:
Pressione parziale del componente i-esimo è la pressione che eserciterebbe il
costituente i se da solo occupasse tutto il volume
Frazione molare:
Frazione molare (%)
In pratica, nota la pressione totale di una miscela di gas (se non e’ nota si puo’
misurare!), la pressione parziale di un qualsiasi componente della miscela e’
sempre calcolabile moltiplicando la pressione totale per la frazione percentuale
di tale componente
210
Fisicaa Applicata, Area Infermieristica , M. Ruspa
In pratica, nota la pressione totale di una miscela di gas (se non e’ nota si puo’
misurare!), la pressione parziale di un qualsiasi componente della miscela e’
sempre calcolabile moltiplicando la pressione totale per la frazione percentuale
di tale componente
Esempio: aria a 15 oC, p = 1 atm, al livello del mare:
Componente
fr. molare
Componente
fr. molare
Azoto (N2)
78,00 %
Argon (Ar)
0,97 %
Ossigeno (O2)
20,93 %
An. Carbonica (CO2)
0.03 %
+ vapore acqueo (0,1 % ÷ 2 %)
p(N2) = 0.78 atm = 593 mmHg
P(02) = 0.21 atm = 160 mmHg
p(Ar) = 0.001 atm = 0.76 mmHg
p(CO2) = 0.0003 atm = 0.23mmHg
211
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SOLUZIONI DILUITE
In una soluzione:
• ni moli di soluto
• no moli di solvente
Soluzione diluita:
ni << no
212
Fisicaa Applicata, Area Infermieristica , M. Ruspa
CONCENTRAZIONE DI UNA SOLUZIONE
%
(grammi soluto / 100 g di soluzione
% vol. (ml di soluto / 100 ml soluzione
g/litro
moli/litro (molarità)
Esempio:
Concentrazione di
soluti nel plasma
totale
213
Fisicaa Applicata, Area Infermieristica , M. Ruspa
DIFFUSIONE LIBERA
Le molecole sia del soluto sia del solvente in una soluzione sono
animate dai moti disordinati di agitazione termica si muovono
in ogni direzione in modo casuale a causa dell’agitazione termica
Si consideri una soluzione con iniziale gradiente di concentrazione
tra due compartimenti
All’equilibrio le
concentrazioni
sono uguali
La migrazione di soluto fino a equilibrare le concentrazioni
avviene per agitazione termica!
214
Fisicaa Applicata, Area Infermieristica , M. Ruspa
OSMOSI
E`un fenomeno di diffusione selettiva attraverso una membrana
semipermeabile (permeabile al solvente ma non al soluto).
All’equilibrio:
Membrana
semipermeabile:
consente il
passaggio di H20
ma non di C6H12O6
C6H12O6
H2O
Se la soluzione e` diluita:
la pressione
idrostatica p=dgΔh è
p π
bilanciata dalla
pressione osmotica
π
π=dgΔh
π·V = δ·nRT
(Van’t Hoff)
• δ = coefficiente di dissociazione elettrolitica (δ=1 per soluto non dissociato)
• a T= costante, π
R = 8,31
è proporzionale a n/V ( = concentrazione moli/litro)
J
K ⋅ mole
= 0.082
litri ⋅ atm
K ⋅ mole
215
Fisicaa Applicata, Area Infermieristica , M. Ruspa
OSMOSI NEI SISTEMI BIOLOGICI
Molte membrane biologiche sono selettive:
• pareti capillari ed intestinali
• membrana alveolare
• membrana cellulare
• tubuli renali
La diffusione di sostanze
dipende dalla differenza di
pressioni idraulica ed
osmotica tra i due lati della
parete
216
Fisicaa Applicata, Area Infermieristica , M. Ruspa
SOLUZIONI ISOTONICHE
Le soluzioni iniettate per via endovenosa devono avere la
medesima pressione osmotica del plasma
soluzioni ISOTONICHE
stessa concentrazione (moli/litro) del plasma
soluzione ipertonica ⇒ atrofizzazione dei globuli rossi
soluzione ipotonica ⇒ emolisi dei globuli rossi
217