ESERCITAZIONE CAMPI 1
Mezzi stratificati: incidenza di onde piane su superfici piane
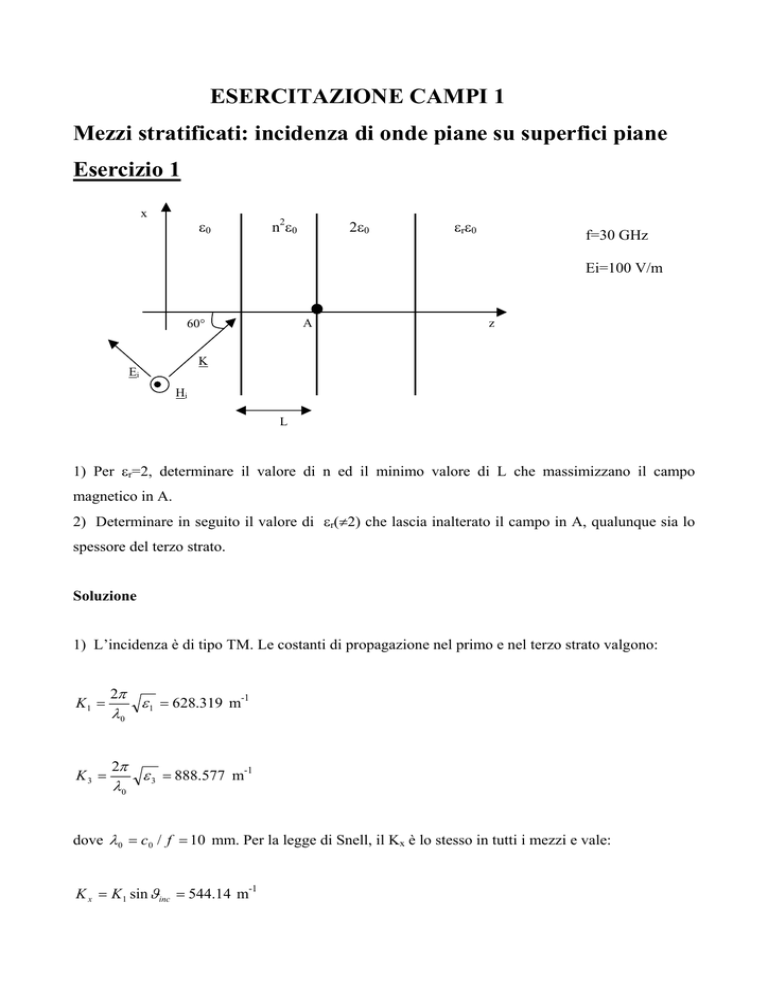
Esercizio 1
x
ε0
n2ε0
2ε0
εrε0
f=30 GHz
Ei=100 V/m
A
60°
z
K
Ei
Hi
L
1) Per εr=2, determinare il valore di n ed il minimo valore di L che massimizzano il campo
magnetico in A.
2) Determinare in seguito il valore di εr(≠2) che lascia inalterato il campo in A, qualunque sia lo
spessore del terzo strato.
Soluzione
1) L’incidenza è di tipo TM. Le costanti di propagazione nel primo e nel terzo strato valgono:
K1 =
K3 =
2π
λ0
2π
λ0
ε 1 = 628.319 m-1
ε 3 = 888.577 m-1
dove λ0 = c0 / f = 10 mm. Per la legge di Snell, il Kx è lo stesso in tutti i mezzi e vale:
K x = K 1 sin ϑinc = 544.14 m-1
Possiamo dunque calcolare le costanti di propagazione delle linee di trasmissione equivalenti a
ciascuno degli strati dielettrici:
K z1 = K12 − K x2 = 314.159 m-1
K z 3 = K 32 − K x2 = 702.481 m-1
Si ha dunque, per le impedenze del modo TM nel primo e terzo strato:
Z TM 1 =
Z TM 3 =
K z1
= 188.111 Ohm
K z3
= 210.315 Ohm
ω ε 0ε 1
ω ε 0ε 3
Dato che il terzo e quarto strato sono omogenei, massimizzare il campo magnetico in A, ossia la
corrente sulla linea di trasmissione corrispondente, equivale a massimizzare la potenza su tale linea.
Pertanto è sufficiente fare un adattamento a λ/4 all’interfaccia fra secondo e terzo strato.
Pertanto l’impedenza della linea di trasmissione corrispondente al secondo strato varrà:
Z TM 2 = Z TM 1 Z TM 3 = 198.904 Ohm
Per ottenere la costante dielettrica corrispondente a tale impedenza, si ha che:
Z TM 2 =
K z2
ω ε 0ε 2
=
K 22 − K x2
ω ε 0ε 2
=
K 02 ε 2 − K x2
ω ε 0ε 2
ed elevando al quadrato si ha:
2
Z TM
2 =
K 02 ε 2 − K x2
(ω ε 0ε 2 )2
Risolvendo questa equazione si ottengono per ε2 due soluzioni:
ε 2,1 = 1.07 ;
ε 2, 2 = 2.508
Dato che è richiesto il valore minimo di L per ottenere campo magnetico massimo in A, dovrò
considerare la soluzione che mi dà la costante dielettrica maggiore, in quanto L è pari ad un quarto
di lunghezza d’onda nella linea corrispondente al secondo strato, e valgono le relazioni:
K z 2 = K 02ε 2 − K x2 ;
λ2 =
2π
;
K z2
e come si vede λ è inversamente proporzionale al Kz, che è a sua volta tanto più grande, quanto più
è grande ε. Pertanto scegliamo come soluzione il valore ε 2 = 2.508 . Si ha quindi:
K z 2 = K 22 − K x2 = 833.012 m-1
λ2 =
2π
= 7.543 mm
K z2
L = λ 2 / 4 = 1.886 mm
2) Ragionando analogamente al caso precedente, devo fare in modo che i due mezzi abbiano la
stessa impedenza, dato che voglio che in A non ci sia riflessione. Quindi devo imporre la
condizione di angolo di Brewster all’interfaccia fra terzo e quarto strato. Si noti che tale condizione
è possibile solo perché ho a che fare con un’onda incidente di tipo TM. Infatti se l’onda incidente
fosse stata TE, non avremmo avuto angolo di Brewster, e quindi non avremmo potuto ottenere
impedenze uguali per nessun valore della costante dielettrica. Si deve avere dunque che, affinché
l’onda incidente all’interfaccia fra terzo e quarto strato incida all’angolo di Brewster:
tan ϑ B =
ε4
ε3
L’incognita nella relazione precedente è proprio la costante dielettrica del quarto strato.
Infatti è possibile ricavare dalla legge di Snell quale sarà l’angolo di incidenza dell’onda
all’interfaccia fra terzo e quarto strato; chiamiamo θi,j l’angolo di incidenza alla j-esima interfaccia.
Risulta ovviamente: θi,j =θt,j-1 , dove θt,j è l’ angolo di trasmissione all’interfaccia j-esima. Per la
legge di Snell si ha:
sin ϑi , j −1 =
ε jµ j
sin ϑt , j −1
ε j −1 µ j −1
Pertanto nel nostro caso si ha:
-
angolo di incidenza alla seconda interfaccia:
⎛ ε2 µ 2
⎞
sin ϑi ,1 ⎟⎟ = 0.5786
⎝ ε 1 µ1
⎠
ϑi ,2 = ϑt ,1 = arcsin⎜⎜
-
angolo di incidenza alla terza interfaccia, ossia angolo di Brewster:
⎛ ε3 µ 3
⎞
sin ϑi ,2 ⎟⎟ = 0.659
⎝ ε2µ2
⎠
ϑB = ϑi ,3 = ϑt ,2 = arcsin⎜⎜
Quindi la costante dielettrica del quarto strato per avere angolo di Brewster vale:
ε 4 = ε 3 tan 2 ϑ B = 1 .2
x
ε0
n2ε0
2ε0
θi2
εrε0
θi3
θt2
θt1
θi1
A
z
K
Ei
Hi
ε0
n2ε0
ZTM1 , Kz1
ZTM2 , Kz2
L
2ε0
A
ZTM3 , Kz3
εrε0
ZTM4 , Kz4
Esercizio 2
ε0,σ
x
ε0
ε1
ε0
f=300 MHz
Ei=1 V/m
ε1=4ε0
z
30°
σ =10-4 S/m
K
Hi
∆=1 cm
Ei
∆
x
Determinare il valore minimo di x per cui la potenza media per unità di superficie dissipata nello
strato di dielettrico con perdite di spessore ∆ sia minima. Determinare inoltre il valore di tale
potenza sia per incidenza TE che per incidenza TM.
Soluzione
La potenza media dissipata per unità di superficie vale:
∆
1
2
Pd = σ ∫ E ( z ) dz
2 0
Le costanti di propagazione dei vari strati valgono:
K1 = K 3 =
K2 =
2π
λ0
2π
λ0
= 6.284 m-1
4 = 12.56 m-1
Il Kx, per la legge di Snell, sarà lo stesso per tutti gli strati:
K x = K 1 sin ϑinc = 3.142 m-1
Da cui le costanti di propagazione nelle linee di trasmissione corrispondenti agli strati dielettrici
varranno:
K z1 = K z 3 = K12 − K x2 = 5.44 m-1
K z 2 = K 22 − K x2 = 12.16 m-1
Poiché si ha, per lo strato con perdite:
σ
= 6 * 10 −3
ωε 0
α≅
K z1σ
= 0.0163m −1
2ωε 1
α∆ = 1.63 * 10 −4 << 1
abbiamo a che fare con piccole perdite, pertanto possiamo considerare E ( z ) costante tra 0 e ∆ e
quindi la potenza varrà:
1
2
Pd = σ E (∆ ) ∆
2
con il campo elettrico calcolato all’interfaccia tra (ε0,∆) ed ε1.
Pertanto minimizzare la potenza dissipata equivale a minimizzare il campo elettrico all’interfaccia,
espresso dalla relazione:
Pd ,min ⇔ E (∆ ) min ⇔ 1 + Γ min
con il coefficiente di riflessione calcolato all’interfaccia tra (ε0,∆) ed ε1.
Passando al modello a linee di trasmissione equivalente alla struttura esaminata, si ha, nel caso di
incidenza TE:
ZTE1
Γ
ZTE2
ZTE3
x
Zin
Devo quindi trovare il coefficiente di riflessione Γ alla sezione indicata (interfaccia tra (ε0,∆) ed ε1)
per poter esprimere il campo elettrico all’interfaccia E(∆), che per le ipotesi fatte di piccole perdite
è anche il campo che si ha in tutto lo strato con perdite di spessore ∆.
Le impedenze del modo TE nelle varie linee sono date da:
Z TE1 = Z TE 3 =
Z TE 2 =
ωµ
K z2
ωµ
K z1
= 435.31 Ohm
= 194.68 Ohm
L’impedenza di ingresso alla sezione indicata è data da (posto T=tanKz2x):
Z in = Z TE 2
Z TE 3 + jZ TE 2T
Z TE 2 + jZ TE 3T
da cui si ha il coefficiente di riflessione (ricordando che ZTE1=ZTE3):
Γ=
2
2
Z in − Z TE1
jZ TE
2 T − jZ TE1T
=
2
2
Z in + Z TE1 2Z TE 2 Z TE1 + j ( Z TE
2 + Z TE1 )T
e quindi:
1+ Γ =
2
2 Z TE 2 Z TE1 + 2 jZ TE
1 + ja T
2T
=
2
2
2 Z TE 2 Z TE1 + j ( Z TE 2 + Z TE1 )T 1 + jbT
a=
con:
Z TE 2
= 0.447
Z TE 1
e
b=
2
2
Z TE
2 + Z TE1
= 1.342
2Z TE 2 Z TE1
Si è visto che minimizzare la potenza dissipata equivale a minimizzare la quantità |1+Γ|, o, che è lo stesso,
la quantità |1+Γ|2. Tale quantità è minima per T→∞. Infatti si ha:
1 + a2T 2
1+ Γ =
1 + b2T 2
2
Annullando la derivata prima rispetto alla variabile T2 per trovare i punti di minimo, si ha:
∂
∂
2
1+ Γ =
2
∂T
∂T 2
⎛1 + a 2T 2
⎜⎜
2 2
⎝1+ b T
(
)
(
)
⎞ a2 1 + b2T 2 − b2 1 + a2T 2
⎟⎟ =
2
1 + b2T 2
⎠
(
)
E tale quantità non si annulla mai se a2≠b2.
K z 2 * x = π / 2 → x = 12 .9cm
Quindi il minimo si ottiene solo per T→∞ (dato che a<b). Da cui si
ha la condizione:
Per la soluzione trovata (tanKz2x=∞) si ha che l’ampiezza del campo elettrico trasmesso vale:
E (∆) min = E i 1 + Γ min = E i
a
0.334V / m
b
Pertanto la potenza media dissipata varrà:
1
2
Pd = σ E (∆) ∆ = 5.56 * 10 −8 Watt
2
CASO DI INCIDENZA TM
In caso di incidenza TM, il campo elettrico avrà anche una componente longitudinale diversa da
zero. Poiché nell’integrale della potenza è presente il modulo quadro di TUTTO il campo elettrico,
per minimizzare la potenza dissipata dovremo minimizzare TUTTO il campo elettrico, ossia la
quantità:
E = Et + Ez
2
2
2
Il campo elettrico traverso vale:
E t = E inc 1 + Γ
2
2
2
dove il coefficiente di riflessione è stavolta calcolato nel caso TM, ossia con le opportune
impedenze di linea, date dall’espressione: ZTM=Kz/(ωε0εr).
Per ottenere l’espressione della componente longitudinale del campo, si utilizza la relazione K⋅E=0,
separatamente per le onde incidente e riflessa (ricordando che tale componente longitudinale
cambia segno nell’onda riflessa). Si ha:
+
+
Kx +
K
Et = − x Etinc
Kz
Kz
−
−
Kx
ΓTM Etinc
− Kz
K ⋅ E = 0 → E z+ = −
K ⋅ E = 0 → E z− = −
Quindi la componente longitudinale totale del campo elettrico vale:
E ztot = −
Kx
(1 − ΓTM ) Etinc
Kz
E devo minimizzare la quantità:
⎡
E = E t + E z = ⎢ 1 + ΓTM
⎢⎣
2
2
2
2
2
⎛K ⎞
+ ⎜⎜ x ⎟⎟ 1 − ΓTM
⎝ Kz ⎠
2
⎤
⎥ Etinc
⎥⎦
2