leve

Esercizi e integrazioni (equilibrio di corpi rigidi estesi, piano inclinato, leve...)
1. La stadera è un tipo di bilancia a bracci di diversa lunghezza; su quello più corto è collegato il piatto, su quello più lungo si
fa scorrere un oggetto di massa nota. Sapendo che il braccio più corto è di 10 cm, che l'oggetto scorrevole ha massa 1 kg e
che è posizionato a 40 cm dal giogo, determina la massa sul piatto.
2. Due sfere pesanti rispettivamente 200 N e 240 N sono appese alle estremità di una sbarra rigida lunga 1,2 m di massa
trascurabile. In quale punto si dovrebbe appoggiare la sbarra su un supporto sottile per avere l'equilibrio?
3. L'asta girevole rappresentata nella figura a fianco non è
evidentemente in equilibrio. Sapendo che ciascun pesetto è di 0,5 N e
che i fori nell'asta sono a distanza di 2 cm l'uno dall'altro, determina
quanti pesetti servono e dove devono essere collocati per riportare l'asta
in equilibrio in posizione orizzontale. Il problema ha un'unica
soluzione?
4. Due oggetti, A e B, di peso diverso, sono appesi agli estremi di un
bastone di legno molto leggero. Si osserva che il bastone così caricato
sta in equilibrio se lo si appende ad un gancio nel punto O, che si trova a
20 cm dal peso A e a 8 cm dal peso B. Quale dei due pesi è più grande?
Qual è il rapporto tra i valori dei due pesi? Applicando un dinamometro
in O si legge che il peso complessivo vale 56 N. Se il peso del bastone è
trascurabile, quanto pesano A e B?
5. Un operaio vuole portare due sacchi di cemento, rispettivamente di 15 kg e di 20 kg, legandoli all'estremità di una sbarra
lunga 1,4 m. Che forza dovrà sostenere? A quale distanza dai due estremi appoggerà la sbarra sulla spalla per tenere in
equilibrio i due sacchi?
6. Una persona di massa 70 kg si trova su di un ponte, fatto di una trave di massa 250 kg e lunga 3,5 metri, stando ad una
distanza di 2 m dal pilone di sinistra. Calcolare le forze F1 e F2 esercitate dai piloni sul ponte.
7. Esamina la situazione descritta in figura. L'asta,
considerata priva di peso, può ruotare attorno al fulcro A.
Quanto vale il peso incognito, se il sistema è in equilibrio?
Cosa cambia se si tiene conto anche che l'asta pesa 8N?
8. Considera la seguente affermazione: Se un pendolo viene spostato dalla sua
posizione di equilibrio, nasce una coppia di forze che tende a riportarvelo.
a) Che cosa si intende in generale per coppia di forze e da quali forze è costituita la
coppia in questo caso? Che cosa si intende per momento di una coppia di forze?
b) Quanto vale il momento di questa coppia se il peso del pendolo è 0,8 N, la
lunghezza del filo è 70 cm e l'angolo tra la direzione del filo e la verticale è 30°?
c) Quale forza si deve esercitare sulla massa del pendolo, in direzione orizzontale, per
mantenerlo in equilibrio nella posizione indicata nella domanda precedente? Quanto
vale in questo caso la tensione del filo?
9. Due blocchi sono collegati per mezzo di una corda, come in figura. La superficie
inclinata forma un angolo di 30˚ con l’orizzontale e il blocco su questa superficie ha
massa pari a 7,5 kg. Trova la massa del blocco pendente che permette al sistema di
rimanere in equilibrio, in assenza di attrito. Risolvi il problema in presenza di attrito,
caratterizzato dal coefficiente 0,2.
Risolvi lo stesso problema nel caso che l'angolo di inclinazione sia di 50°.
10. Determina la massima inclinazione che può avere un tratto di strada per consentire il parcheggio di un’automobile, se il
coefficiente di attrito statico fra pneumatici e asfalto vale 0,3. Schematizza la rampa con un piano inclinato, l’auto con un
blocco su di esso appoggiato.
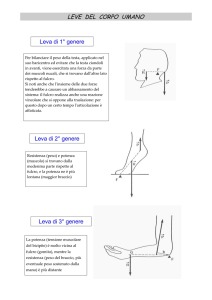
Le leve.
Si chiamano macchine semplici dispositivi come leve, carrucole e piani inclinati mediante i quali si può equilibrare (ed
eventualmente spostare) una forza resistente mediante una forza motrice di intensità diversa. In particolare nelle leve trovano
applicazione le condizioni di equilibrio rispetto alle rotazioni, descritto attraverso i momenti delle forze. Il punto di appoggio
(attorno a cui avviene la rotazione) si chiama fulcro e le distanze dei punti di applicazione si chiamano bracci. Il rapporto tra
la forza resistente e la forza motrice si chiama vantaggio della leva.
Si ha una leva di primo genere quando il fulcro si trova tra il punto di applicazione della forza motrice 
F e quello della
d

d
forza resistente 
, cioè se il fulcro è più vicino al punto di
R . Essa è vantaggiosa solo se 
F 
R ossia se
F
R
applicazione della forza resistente che a quello della forza motrice.
Si ha una leva di secondo genere quando il punto di applicazione della forza resistente si trova tra il fulcro e il punto di
applicazione della forza motrice. Una leva di secondo genere è sempre vantaggiosa.
Si ha una leva di terzo genere quando il punto di applicazione della forza motrice si trova tra il fulcro e la forza resistente.
Una leva di terzo genere è sempre svantaggiosa.
Individua il genere di leva a cui si può ricondurre ciascuna delle situazioni illustrate:
Una trave come bilancia
Una trave rigida di lunghezza L = 6 m e massa M = 360 kg è
appoggiata su un sostegno di altezza h = 50 cm a 1/3 della sua
lunghezza; per stare orizzontale l’estremo più vicino al
sostegno è fissato al pavimento con una molla la cui lunghezza
di riposo è metà di quella attuale.
1. Determinare la costante elastica della molla.
2. Determinare la forza vincolare garantita dal sostegno.
Se un bambino sale sull’estremo libero della trave, questo si
abbassa di un tratto pari a 1/5 dell’altezza del sostegno.
3. Quanto pesa il bambino?
Note: Le dimensioni della sezione della trave sono trascurabili
rispetto alla lunghezza. Assumere inoltre,in ogni caso, che
l’angolo formato dalla trave con il piano orizzontale sia piccolo.