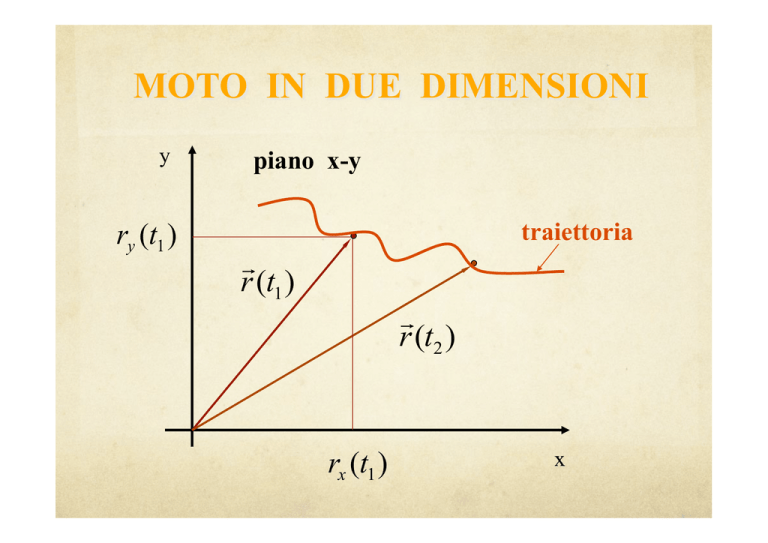
MOTO IN DUE DIMENSIONI
y
ry (t1 )
piano x-y
traiettoria
r (t1 )
r (t2 )
rx (t1 )
x
Velocità vettoriale
y
Δr = r (t2 ) − r (t1 )
v(t1 )
r (t1 )
Δr r (t 2 ) − r (t1 )
vm =
=
Δt
t 2 − t1
vm
Δr
r (t2 )
v(t 2 )
x
Δr
vi = lim
Δt →0 Δt
dr
=
dt
Accelerazione vettoriale
Δ
v
v
(
t
)
−
v
(
t
)
2
1
Δv = v (t2 ) − v (t1 )
am =
=
Δt
t 2 − t1
vi (t1 )
y
r (t1 )
Δv
r (t2 )
vi (t2 )
x
Δv
ai = lim
Δt →0 Δt
dv
=
dt
accelerazione tangenziale e radiale
y
ar
traiettoria
at
at
ar
at
a
ar
a
a = ar + at
x
modulo velocità
acc. tangenziale
cambia
acc.
radiale
direzione velocità
Equazioni vettoriali
y
ry
r
j
i
rx
x
r = rx i + ry j
dr drx dry
v=
=
i+
j = vx i + v y j
dt dt
dt
dv dv x dv y
a=
=
i+
j = ax i + a y j
dt
dt
dt
a x
rx
v x
r → ry v → v y a → a y
a
r
v
z
z
z
vx = v0 x + a xt
v = v0 + at ⇒ v y = v0 y + a y t
vz = v0 z + a z t
Coordinate intrinseche
Il vantaggio della notazione vettoriale sta nel fatto che è indipendente dal sistema di
coordinate,
e quindi permette di scrivere in maniera semplice le equazioni senza preoccuparsi di
definire un sistema di coordinate.
Consideriamo
s coordinata curvilinea
ds
v = u t = vu t
dt
Coordinate intrinseche
accelerazione
ds
v = u t = vu t
dt
dv d 2r
a=
=
dt dt 2
a=
d (vu t ) dv
du
dv
dΦ
= ut + v t = ut + v
un
dt
dt
dt
dt
dt
dΦ dΦ ds 1
=
= v
dt
ds dt R
a=
Accelerazione
tangenziale
dv
dΦ
dv
v
ut + v
un =
ut + 2 u n = at + a n
dt
dt
dt
R
Accelerazione normale
o centripeta
Moto circolare
ϑ (t ) = s(t ) R
y
ut
un
x(t ) = R cos ϑ (t )
y (t ) = R sen ϑ (t )
s
θ
O
R costante!
x
Moto circolare uniforme
ha accelerazione normale alla traiettoria
dω
v
a=R
ut + 2 u n = at + a n
dt
R
dϑ (t ) 1 ds v
ω (t ) =
=
=
dt
R dt R
s(t ) = s0 + vt
ϑ (t ) = ϑ0 + ω t
Moto periodico
con periodo
2πR 2π
T=
=
v
ω
Moto circolare
ϑ (t ) = s(t ) R
y
ut
un
x(t ) = R cos ϑ (t )
y (t ) = R sen ϑ (t )
s
θ
O
R costante!
x
Moto circolare uniforme
ha accelerazione normale alla traiettoria
dω
v
a=R
ut + 2 u n = at + a n
dt
R
dϑ (t ) 1 ds v
ω (t ) =
=
=
dt
R dt R
s(t ) = s0 + vt
ϑ (t ) = ϑ0 + ω t
Moto periodico
con periodo
2πR 2π
T=
=
v
ω
Moto circolare
Esempio
Il rotore di una centrifuga ruota a 3000 giri/min. A quanti radianti al secondo
equivale questa velocità angolare?
Sapendo che il rotore ha un diametro di 30 cm, calcolare il modulo della velocità
tangenziale e dell'accelerazione centripeta.
Un giro del rotore è uguale a 2π radianti, dunque la velocità angolare è:
ω = 3000 2π (rad/min) = 6000π rad/min = 100π rad/sec.
Il modulo della velocità tangenziale è ω r:
v = (2π r / T) = ω r da cui si ottiene: v = 100π rad/sec 0,15 m = 15π m/sec
Il modulo dell'accelerazione centripeta è ω2r=v2/r=15000m/sec2.
Lancio con velocità orizzontale
Il pacco lanciato dall aereo
MOTO DEL PROIETTILE
a y = − g
v y = v 0 y − gt
y = y 0 + v 0 y t − 1 gt 2
2
v x = v0 x
x = x 0 + v0 x t
y
x
• accelerazione g costante
verso il basso
• no resistenza aria
moto con traiettoria
parabolica
Lancio con velocità verticale
g
a = − gyˆ
java
y
θ =0
ymax
v0 y
vy
v0
vy = 0
θ
v0 x
v0 x
traiettoria parabolica
v0 x
vy
θ0
v0 x
v0 x
vy
gittata
x
Moto parabolico
Equazione della traiettoria
x(t ) = v0 cos θ t
y (t ) = v sinθ t − 1 gt 2
0
2
x
t
=
v cos θ
0
x
1
x
y = v0 sinθ
− g
v0 cos θ 2 v0 cos θ
Moto di tipo parabolico
2
g
2
= x tgθ −
x
2v02 cos 2 θ
Lancio con velocità verticale
Lancio con velocità verticale
Moto parabolico
Ricordiamo il caso unidimensionale
dx
v=
dt
t
⇒
x(t ) = x0 + v(t )dt
∫
t0
asse x
asse y
t
x(t ) = x(0) + v x (t )dt = v0 cos θ t
0
t
y (t ) = y (0) + v (t )dt = v sinθ t − 1 gt 2
y
0
2
0
∫
⇒
∫
Moto parabolico
Equazione della traiettoria
x(t ) = v0 cos θ t
y (t ) = v sinθ t − 1 gt 2
0
2
x
t
=
v cos θ
0
x
1
x
y = v0 sinθ
− g
v0 cos θ 2 v0 cos θ
Moto di tipo parabolico
2
g
2
= x tgθ −
x
2v02 cos 2 θ
Moto parabolico
Calcolo di gittata e massima
quota raggiunta
dall oggetto
g
2
y = x tgθ − 2
x
2v0 cos 2 θ
per il calcolo della
gittata OG impongo y=0
e ottengo
2v02 cos 2 θ tgθ 2v02 cosθ sin θ
x=
=
g
g
notiamo che il massimo viene
raggiunto per il valore
v02 cosθ sin θ
x =
g
2
2
v
sin
θ
y = 0
2g
Moto parabolico
Esempio
Un arciere lancia una freccia in aria con un'inclinazione di 60 gradi, ad una distanza di 36 metri
da un bersaglio posto a 2 metri dal suolo. La freccia viene scoccata da un'altezza di 1.5 metri dal
terreno e con una velocità iniziale, V0 di 20 m/s . Verificare se la freccia riesce a colpire il
bersaglio.
Soluzione:
Incognite:
tvolo (tempo necessario affinché la freccia copra la
distanza di 36 metri);
y(tvolo) (altezza della freccia dopo i 36 metri di volo);
Per determinare la velocità iniziale della freccia:
Per il calcolo del tempo di volo tvolo:
Per determinare V0y:
Per determinare y(tvolo):
V0x= V0*cos(θ)
Quindi V0x= 10 m/s
tvolo=x/V0x=36m/10m/s=3.6 s
V0y = V0.sen(θ)= 17 m/s
y(tvolo) = (V0y*tvolo) + (1/2g*tvolo2 )= (17 m/s *3.6 s) +(- 4.9 m/s2 * 13 s2) = -2.3 m
Dal risultato negativo si deduce che la freccia cade in anticipo e quindi il bersaglio non viene colpito. Affinché
il bersaglio venga colpito y(t) avrebbe dovuto essere uguale a 0.5 m.











